计算机意义上的数据结构总的来说,分为以下两种,线性结构和非线性结构.对于线性结构,我们有时也叫做线性表,它的特点是它里面的任何元素(结点)都只有一个前驱(头结点除外)和一个后继(尾结点除外).二叉树之所以是非线性结构,就是因为它的每个结点只能有一个前驱,却可以有两个后继.而链表和顺序表就符合这个要求.并且,线性表按照存储方式的不同可以分为链表和顺序表这两种.按照种类的不同可以分为数组,栈,队列,字符串等.
其中栈和队列都是属于受限的线性表.所谓受限,指的是他们在元素的增删上受到了额外的限制.栈的限制是只能在顶部增删元素,不能随意增删栈内的任意元素.类似地,队列的限制是只能在线性表的头部和尾部进行元素的增加和删除,而且规定头部只能进行删除,尾部只能进行增加.
这种受限的结构弱化了线性表的增删范围,但保留了O(1)的增删效率(对于顺序表来说还是一种增强).并且因为他们的存取特性可以用来解决一些特定的问题.我们这里只讲队列.
和其他的线性表一样,队列按照存储方式的不同又可以分为顺序队列和链式队列.顺序队列是一种定长的数组结构.我们平时所说的数组LinkedList,它的add()和poll()就是按照队列的方式进行的.因为add()是向队尾增加一个元素,而poll()是向队头拿走一个元素.
队列数据结构的设计基本是这样的:
设计两个指针front和rear,他们分别指向队头和队尾,当我们增加一个元素时,rear向后移动1位,指向新的队尾元素,当我们删除一个元素时,front向后移动一位.当front == rear时,说明这个队列为空.设计队头队尾指针的目的是为了避免在增加和删除的时候时间复杂度为O(n).下面来看:
如果没有指针,那么增加一个元素
假设现在一个队列里装了1,2,3,4.现在要增加一个元素5.因为没有指针,元素5就要从头开始搜索队列的第一个空位置,这个过程的时间复杂度为O(n).
- [增加元素图示] List item
类似的,假设现在一个队列时装了1,2,3,4,5.现在要删除元素,按照队列的特点,只能删除队头的元素,也就是1.如何才能算删除了,按照数组的写法,所谓的删除事实上是一种覆盖,也就是1之后的元素依次覆盖前面的元素,最后5被null所覆盖.这个时间复杂度也是O(n). - [删除元素图示] List item
如果元素的增删还是O(n),那么栈和队列和普通的顺序表也没有什么区别,实在没必要多此一举.所以设计双指针对于队列来说是非常必要的,因为这样以来,就可以把增删操作的时间复杂度和链表保持一致,也就是说,具备了普通链表的增删效率.
因为增加一个元素就让rear指针后移一位,删除一个元素就让front指针后移一位,指针的后移只是一个O(1)操作,但是却保证了增删的过程中不涉及到所增删元素以外的元素变动.当我们对这个队列遍历的时候,实际上我们只遍历front后面一直到rear所指的元素为止,换言之,front及front之前的元素就不会被遍历了,这几变相实现了元素的删除操作.当我们增加元素时,我们只要在rear之后的空位覆盖上这个元素即可,如果没有指针,我们就无法立刻确定元素应该在哪个位置插入.
但我们同时注意到,每一次的删除都会导致front后移,而队列的长度有限(这里指的时顺序队列,它的长度是要一开始就确定的).所以每一次删除,等同于少了一个长度,即使我们可以再增加元素,也不能超过这个队列的最大长度.但是我们曾经删除的元素留下来的空位是无法利用的,这就造成了空间浪费.解决这个问题,有两种方法:
第一种是让这个队列的长度足够长,但这实际上是更大的资源浪费,这里主要为了能够容忍更多的删除操作所导致的长度减小,使得队列的长度足够应付对应问题的数据量.
第二种是采用循环队列对这种单顺序表结构进行改造.循环队列的特点将在下面介绍.
接下来是我手写的顺序队列的代码(python):
#构造一个线性队列及其相关操作
class SequenceQueue():
def __init__(self):
self.MaxQueueSize = 10
self.s = [None for x in range(0, self.MaxQueueSize)]
self.front = 0
self.rear = 0
def IsEmptyQueue(self):
if self.front == self.rear:
iQueue = True
else:
iQueue = False
return iQueue
#Enter the SequeceQueue
def EnQueue(self, x):
if self.rear == self.MaxQueueSize-1:
print("The SequenceQueue is full.")
return
else:
self.rear = self.rear + 1
self.s[self.rear] = x
#Exit the SequenceQueue
def ExQueue(self):
if self.IsEmptyQueue():
print("The SequenceQueue is empty.")
return
else:
self.front = self.front + 1
return self.s[self.front]
#get the head of sequencequeue
def GetHead(self):
if self.IsEmptyQueue():
if self.IsEmptyQueue():
print("The SequeceQueue is empty.")
return
else:
return self.s[self.front+1]
def CreateQueueByInput(self):
data = input("Please input the element(to end the input by pressing '#'): ")
while data != '#':
self.EnQueue(data)
data = input("Please input the element: ")
print("The SequenceQueue is created successfully!")
def GetQueueLength(self):
print("The present SequenceQueue's length is:",self.rear - self.front)
return self.rear - self.front
#traverse in the queue
def QueueTraverse(self):
if self.IsEmptyQueue():
print("The final SequenceQueue is empty.")
return
else:
print("The final SequenceQueue is: ", end='')
for i in range(self.front+1, self.rear+1):
print(self.s[i], end=' ')
#seek the target element's index
def findElement(self, element):
if(self.front == self.rear):
print("The SequenceQueue is empty!")
return
for i in range(self.front+1, self.rear+1):
if self.s[i] == element:
print("The target element is first occured in the index of", i-self.front-1 ,"of the SequenceQueue.")
return
print("The target element does not exist in the SequenceQueue!")
当时写的时候想锻炼以下自己的英语表达,所以几乎都是英文描述,不过其实也不难理解.因为无非就是一些基础的增删改查而已.
循环队列
前面有说过,一般的顺序队列由于头指针和尾指针的移动都是单向的,而且不能够超过队列的最大长度,所以如果要进行的删除操作比较频繁,不能再次利用到的空间也就越多,这回造成内存空间的无端浪费,解决这个问题可以通过改进队列的结构为循环队列.
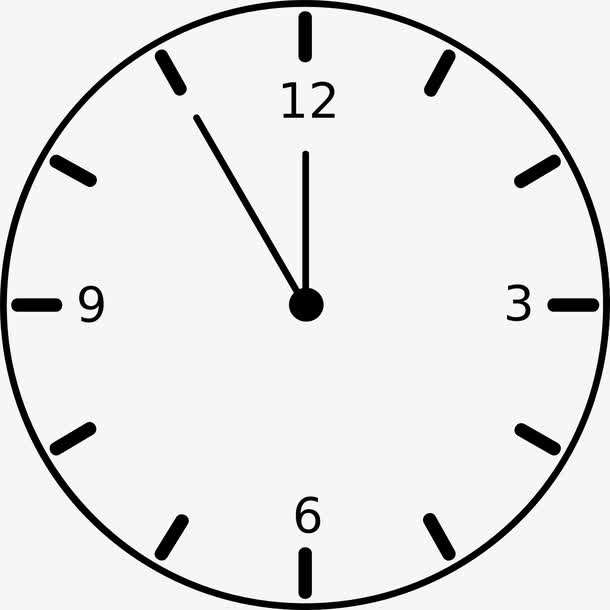
一般来说,书上只要涉及到循环队列都会给我们一个很直观的环状结构,就比如下图

其实这样的描述非常地直观,我们可以认为循环队列就是这个样子的.但事实上,一切的数据结构图只是我们的主观臆想,为的是方便我们理解,循环队列也是如此.我们当然可以这么理解,但它的底层实现却不是一个这样的环形,事实上,它是利用了我们经常在数学上用到的模运算.
根据普通顺序队列的原则,当增加一个元素时,rear += 1,当rear == length - 1的时候,就无法再对队列执行增加操作.但现在,我们利用求模运算,在队列还有空位的前提下,可以继续对rear执行增操作.只不过为了对应队列中的对应位置,需要将rear % length(队列长度).比如一个长度为12的队列,当rear增加到15时, 15 % 12 == 3,它就对应队列从头指针开始的第三个元素,那么有人可能要问了,头在何处,其实头就是这个队列所具有的一个数组,头的位置就是数组索引为0的位置.按照我们的想法我们可以让头尾相连形成一个环形结构,然后rear按照顺时针走动循环往复,但是计算机是无法理解的,这样的想法也不能让计算机接受.所以其本质上是rear走到了数组最大索引以后再返回到头部索引.这样的返回操作只有通过模运算来实现,如果假设数组的索引有0, 1, 2, … n-1.那这个模就是n.当rear增加到n是,事实上就是返回到了0.这个思想在计算机组成原理里经常提及,因为存储器的内存也是有限的,这个方法可以让指针向钟表的指针一样按照顺时针方向循环地走下去,如果不是队列已满,理论上rear可以不停地走下去.当然front也是.
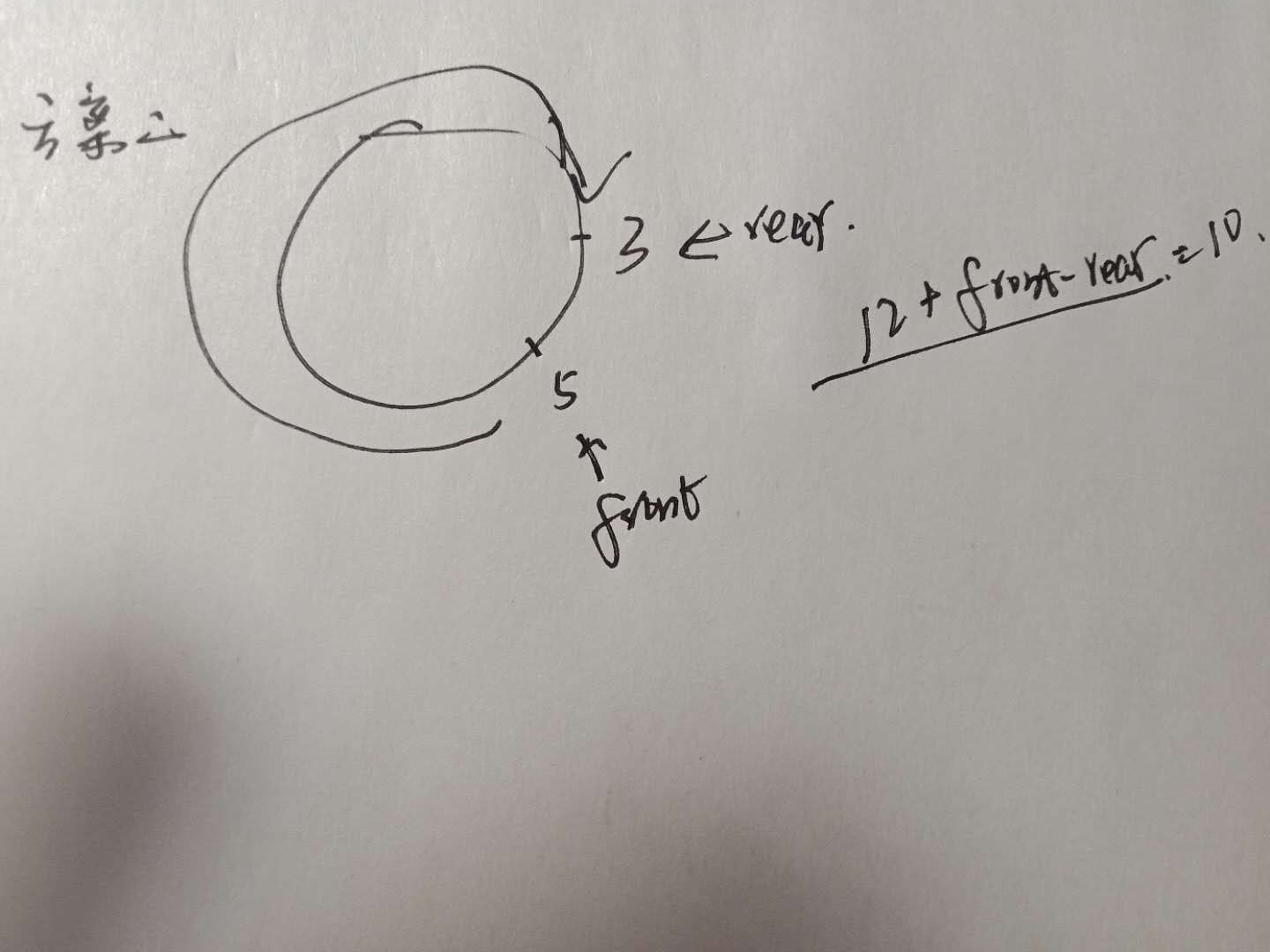
在循环队列的增加和删除操作中需要注意:当删除的时候,front += 1, 当增加的时候rear += 1.此时队列的长度为rear - front.等等,真的是这样吗?在正常顺序队列的确是如此,可不要忘了在这个循环队列中是会容易出现下面这种情况的:
就拿时钟打比方,如果rear指针指向3, 而front指针指向5,那么rear-front<0.难道说此时队列的长度为-2吗?这显然是不对的.
当rear - front出现负值的情况时,我们要的并不是这个负值,而是一个类似于补码的概念,我们想像一下从front到rear可以怎么走,最近的路径是由front指向rear,但这个方向跟front和rear的行走方向相反,所以就会出现负值.路可以这么走,但长度不可能存在负值,所以尽管这条路最短,仍然不可取,因为我们的front和rear方向是唯一的.那么只能让front沿着它的前进方向走到rear了.这样的路径长度y = rear - front + length.(length表示这个线性表的最大长度)

鉴于此,我们就不能单纯地通过rear - front来判断队列的长度了.而应该判断rear和front的大小.因为rear和front都很有可能大于队列的最大容量length.所以如果写成rear % length 和front % length是最好的.
下面是我手写的关于循环队列的增删改查,时间久远了,可能会有错误,如有请指出,非常感谢.
class CircularSequenceQueue():
def __init__(self):
self.MaxQueueSize = 10
self.s = [None for x in range(0, self.MaxQueueSize)]
self.front = 0
self.rear = 0
self.fsq = []
def IsEmptyQueue(self):
if self.front % self.MaxQueueSize == self.rear % self.MaxQueueSize:
iQueue = True
else:
iQueue = False
return iQueue
def EnQueue(self, x):
if (self.rear+1) % self.MaxQueueSize != self.front % self.MaxQueueSize:
self.rear = (self.rear+1) % self.MaxQueueSize
self.s[self.rear] = x
else:
print("The Queue is full.")
return
def ExQueue(self):
if self.IsEmptyQueue():
print("The Queue is empty.")
return
else:
self.front = (self.front+1) % self.MaxQueueSize #将front后面的下标赋给front
return self.s[self.front]
def CreateQueueByInput(self):
data = input("Please input the element(to end the input by pressing '#'): ")
while data != '#':
self.EnQueue(data)
data = input("Please input the element: ")
def GetHead(self):
if self.IsEmptyQueue():
print("The SequenceQueue is empty.")
return
else:
return self.s[(self.front+1)%self.MaxQueueSize]
def GetQueueLength(self):
if(self.rear%self.MaxQueueSize < self.front%self.MaxQueueSize):
return self.rear % self.MaxQueueSize - self.front % self.MaxQueueSize + self.MaxQueueSize;
else:
return self.rear % self.MaxQueueSize - self.front % self.MaxQueueSize;
接下来用这个循环队列解决一个经典的约瑟夫问题:
旅游团今日搞了一个优惠活动,他让所有参团的人围成一个圈,然后从第一个人开始报数,当有人报到3的时候,那个人出列,然后下一个人继续从1开始报数.当最后只剩下一个人的时候,这个人就可以免单.现在有50个人按照从1到50的顺序编好了号,请问最后谁能够获得免单?
这是一个做了改动的约瑟夫问题.
解决方法是将这1-50按顺序存入一个长度>= 53的循环队列中,然后设计一个指针ptr用于遍历这个队列,设计一个num用于计数.如果num < 3,那么就将遍历到的元素增加到队尾中,然后删除这个元素.如果num == 3,那么只删除这个元素,然后num在下一次遍历的时候置1,按照这个过程一直进行下去,直到最后队列中只剩下一个元素为止.这个数字所代表的人即是最后可以免单的幸运儿.
def JosephProblem(self, totalNum, kNum):
# 将从1到totalNum的数字依次存入循环队列中
for i in range(1, totalNum+1):
self.EnQueue(i)
num = 1
while(self.GetQueueLength() > 1):
while(num < 3):
self.EnQueue(self.GetHead())
self.ExQueue()
num += 1
if(num == 3):
self.ExQueue()
num = 1
print(self.s)#打印每次删除一个元素以后的队列情况
print("最后留下来的人的编号是:", self.s[self.rear])
我们先以20为例,检查一下有没有错误,如果计算正确的话,最后留下来的人的编号应该是20号.
计算方式如下:
从1开始,按照自然顺序,找到能被3整除的数,因为最后只能留下一个数,所以需要删除19个数.因此找到19个能被3整除的数,它们分别是3, 6, 9, … 3+18*3=57.
将这些数分别对20求余,得到的数为3, 6, 9, …, 18, 1, 4, …,17.这19个数去掉以后的数就是最后应该留下的数.
参考结果如下:
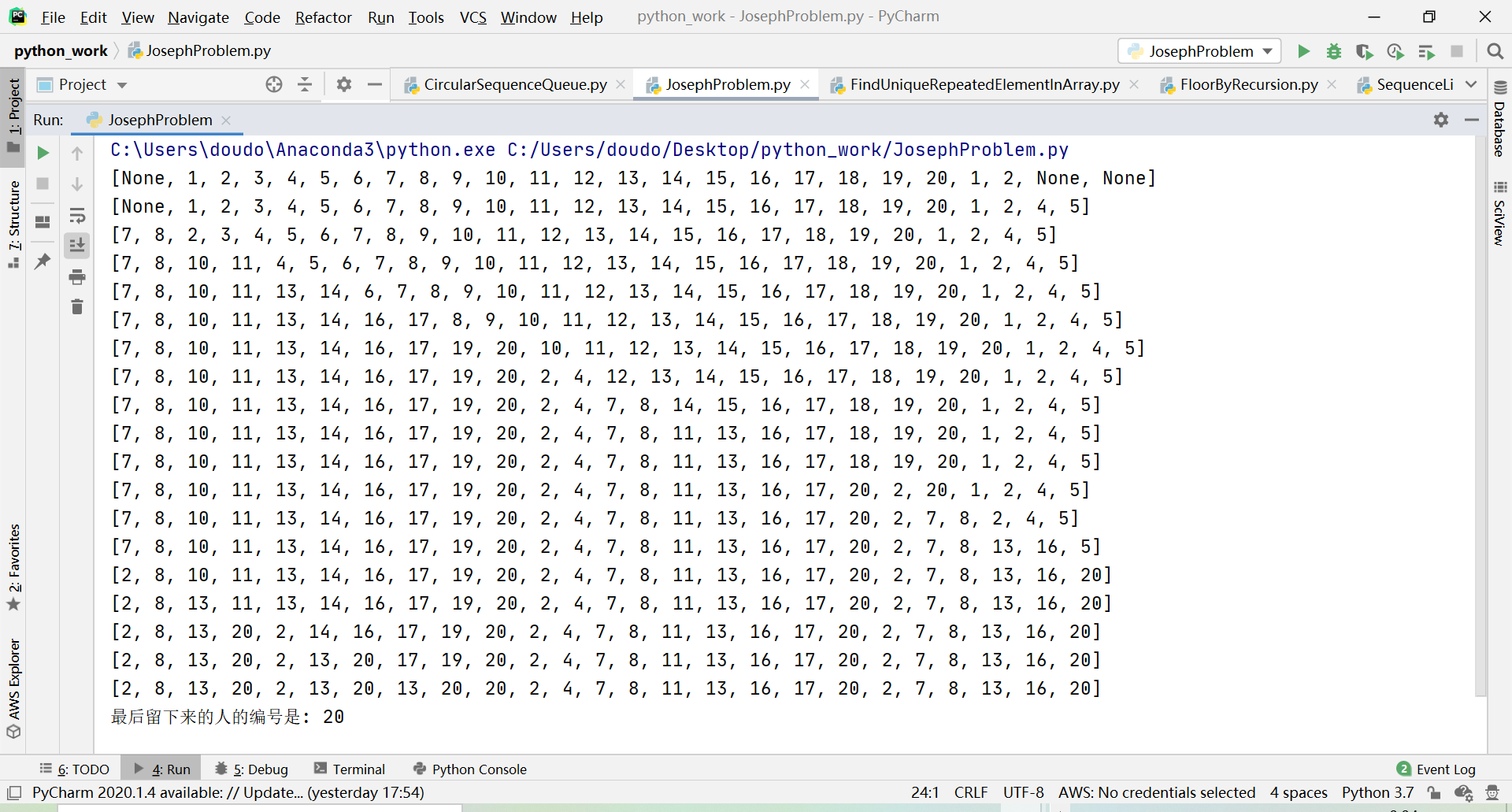
再把50作为实参传入,记得还要修改一下init()函数里面队列的最大容量.
最后求出的结果为11.
以上就是顺序队列的结构和循环队列的结构.还有一个是链式队列.其实链式队列更为方便,无论是在增删方面的效率还是内存空间的利用率都是极好的.
这里就先贴出吧.
同时它解决约瑟夫问题也是相当容易.
#To get the free Travelling quality, Josephus has to play a game.A group of
#visitors(number of people is 40)stand in a circle and speak number from 1 in begin,
#if one has spoken 3,he or she will exit the queue, then the next one speak from 1
#in begin, so as before.
#Each round exit one until there is only one ramain,which can travel in free.
#Josephus chooses to stand in the number of 31, will he get the free quality?
class QueueNode():
def __init__(self):
self.data = None
self.next = None
class LinkQueue():
def __init__(self):
self.head = QueueNode()
self.front = self.head
self.rear = self.head
def IsEmptyQueue(self):
if self.front == self.rear:
iQueue = True
else:
iQueue = False
return iQueue
def EnQueue(self, da):
cNode = self.head
while cNode.next != None:
cNode = cNode.next
cNode.next = QueueNode()
cNode.next.data = da
self.rear = cNode.next
def DeQueue(self):
if self.IsEmptyQueue():
print("The Queue is empty!")
return
else:
cNode = self.front.next
self.front.next = cNode.next
if self.rear == cNode:
self.rear = self.front
return cNode.data
def GetHead(self):
if self.IsEmptyQueue():
print("The queue is empty.")
return
else:
return self.front.next.data
def GetQueueLength(self):
if self.IsEmptyQueue():
print("The queue is empty.")
return
else:
length = 0
tNode = self.front
while tNode != self.rear:
tNode = tNode.next
length += 1
return length
def QueueTraverse(self):
if self.IsEmptyQueue():
print("The queue is empty.")
return
else:
tNode = self.front
while tNode != self.rear:
tNode = tNode.next
print(tNode.data,end=" ")
print()
def Josephus(self, n, k):
qu = LinkQueue()
i = 1
while i <= n:
qu.EnQueue(i)
i = i + 1
print("The rank of number in queue is:")
qu.QueueTraverse()
print("nThe rank of number in exiting the queue is: ")
count = 0
while qu.GetQueueLength() != 1:
iNum = 1
while iNum != k:
tData = qu.DeQueue()
qu.EnQueue(tData)
iNum = iNum + 1
print(qu.DeQueue(), end=" ")
count = count + 1
if count%10 == 0:
print()
print("nThe number be remained in final is: ", end=" ")
qu.QueueTraverse()
def TestJosephus(self):
PeopleNum = int(input("Please input the number of total people: "))
Gap = int(input("Please input the number of which is to be out of the Queue: "))
if PeopleNum > 0 and Gap > 0 and Gap <= PeopleNum:
self.Josephus(PeopleNum, Gap)
else:
print("The input does not fit the requirement.")
jp = LinkQueue()
jp.TestJosephus()
下面是总结.

晚安!
最后
以上就是炙热荷花最近收集整理的关于数据结构之队列(python实现)的全部内容,更多相关数据结构之队列(python实现)内容请搜索靠谱客的其他文章。








发表评论 取消回复