简述
epsilon-Greedy算法(
ϵ
-贪婪算法)算是MBA(Multiarmed Bandit Algorithms)算法中最简单的一种。因为是MBA算法介绍的第一篇,所以在这里还是先简单说明下MBA。当然,要解释MBA,首先就得EE问题(Explore-Exploit dilemma)。
什么是EE问题呢? 这两个”E”,其中一个代表“exploit”,中文可译作“利用”;另一个代表“Explore”,中文可译作“探索”。结合一个例子可能更方便对EE,及MBA作一个简单的解释。如果之前已经有了解了的,建议直接跳过下面这段。
现在假如你面前有n台老虎机,每台老虎机吐钱的概率不一样。你并不清楚每台老虎机的吐钱的概率分布。那么,如果你想要最大化收益,你该怎么办呢? 通常来说,你内心可能有两种好的决策:1、找到某一台收益还不错的老虎机,然后坚持摇这台老虎机;2、不断尝试探索新的老虎机。这个探索的过程中,可能发现更好的老虎机,当然也要承担摇差的老虎机带来损失的风险。显然,第一种对应的就是“exploit”,第二种对应“explore”,而bandit算法就是要解决这种EE问题,实现最大化收益。
ϵ
-贪婪算法是如何在“exploit”和“explore”之间实现权衡,以尽可能实现最大化收益的呢? 首先,从算法的名称我们知道,这是一种贪婪的算法。纯粹贪婪的算法,放到这种多臂老虎机的场景来看就是每次都选择当前那个最好的臂摇,即使从长远来看可能非常不好。那么,
ϵ
-贪婪算法和贪婪算法的区别在哪呢? 就像它的名字所展示的那样,区别仅仅就在这个
ϵ
。这个
ϵ
代表执行执行“探索”的概率。比如设置
ϵ
=0.1,那么就表示有10%的概率会进行“探索”操作,而90%会进行“利用”操作,也就是摇当前最好的臂。如果以摇老虎机臂的过程,用次数来算的话,也就是,每10次操作,仅有1次操作去进行探索——尝试其他的臂。
原理是不是很简单。下面是更正式点的定义:
提问:如果 ϵ 分别设置为0,1,它们分别表示什么情况?
代码
以下是相关代码:
import random
def ind_max(x):
m = max(x)
return x.index(m)
class EpsilonGreedy():
def __init__(self, epsilon, counts, values):
self.epsilon = epsilon
self.counts = counts
self.values = values
return
def initialize(self, n_arms):
self.counts = [0 for col in range(n_arms)]
self.values = [0.0 for col in range(n_arms)]
return
def select_arm(self):
if random.random() > self.epsilon:
return ind_max(self.values)
else:
return random.randrange(len(self.values))
def update(self, chosen_arm, reward):
self.counts[chosen_arm] = self.counts[chosen_arm] + 1
n = self.counts[chosen_arm]
value = self.values[chosen_arm]
new_value = ((n - 1) / float(n)) * value + (1 / float(n)) * reward
self.values[chosen_arm] = new_value
return代码来源: https://github.com/johnmyleswhite/BanditsBook.
效果简单分析
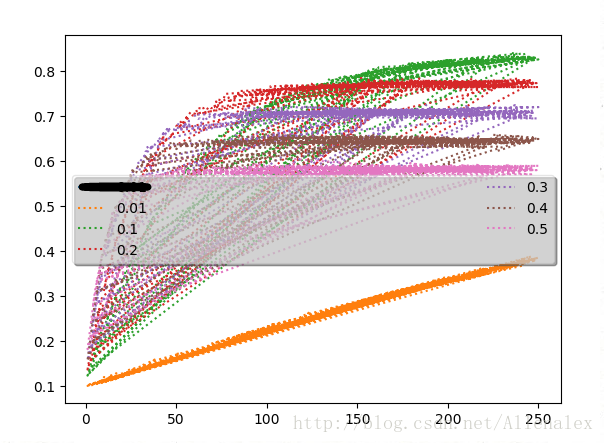
上图是我基于Bandit Algorithms for Website Optimization上的实验画的一个模拟老虎机摇臂操作的图。总共5个臂,一次实验摇臂250次,总共执行了50000次(具体参考Bandit Algorithms for Website Optimization上的实验)。其中。横轴为摇臂次数,纵轴为平均收益。
ϵ
从取值[0.01,0.1,0.2,0.3,0.4,0.5],图中可以看到:
1、
ϵ
设置的越高,收敛到最佳收益的速度越快。这个很好理解。随机探索的概率越大,越能更快的探索到最好的臂。
2、在0.1-0.5,
ϵ
设置的越低,最终的平均收益越高。这个也是比较好理解的。每次都很大概率的随机探索,就会存在很多利用效果不好的臂的情况。但我们看到,设置0.01的时候,这个最终的收益是非常差的。(实际书中只包括了0.1-0.5的实验,0.01是我自己加上去的)
参考文献:Bandit Algorithms for Website Optimization
最后
以上就是幸福芒果最近收集整理的关于bandit算法(1)--epsilon-Greedy Algorithm(附代码)的全部内容,更多相关bandit算法(1)--epsilon-Greedy内容请搜索靠谱客的其他文章。








发表评论 取消回复