k 臂赌博机
- 环境
- DiscreteActionEnv
- k 臂赌博机
- 策略
- ε varepsilon ε 贪婪
- UCB
- 实验
- 参考
环境
k 臂赌博机有 k 个拉杆,每个动作选择其中一个拉杆进行游戏,之后会收到一个数值奖励,玩家的目标是在一段时间内最大化预期的总奖励。
我们继承离散型的环境模型:
DiscreteActionEnv
/**
* To use the dummy environment, one may start by specifying the state and
* action dimensions.
* Eg:
* @code
* DiscreteActionEnv::State::dimension = 4;
* DiscreteActionEnv::Action::size = 2;
* @endcode
*
* Now the DiscreteActionEnv class can be used as an EnvironmentType in RL
* methods just as any other mlpack's implementation of gym environments.
*/
class DiscreteActionEnv
{
public:
/**
* Implementation of state of the dummy environment.
*/
class State
{
public:
/**
* Construct a state instance.
*/
State() : data(dimension)
{ /* Nothing to do here. */ }
/**
* Construct a state instance from given data.
*
* @param data Data for the state.
*/
State(const arma::colvec& data) : data(data)
{ /* Nothing to do here */ }
//! Modify the internal representation of the state.
arma::colvec& Data() { return data; }
//! Encode the state to a column vector.
const arma::colvec& Encode() const { return data; }
//! Dimension of the encoded state.
static size_t dimension;
private:
//! Locally-stored state data.
arma::colvec data;
};
/**
* Implementation of discrete action.
*/
class Action
{
public:
// To store the action.
size_t action = 0;
// Track the size of the action space.
static size_t size;
};
/**
* Dummy function to mimic sampling in an environment.
*
* @param * (state) The current state.
* @param * (action) The current action.
* @param * (nextState) The next state.
* @return It's of no use so lets keep it 0.
*/
double Sample(const State& /* state */,
const Action& /* action */,
State& /* nextState*/)
{ return 0; }
/**
* Dummy function to mimic initial sampling in an environment.
*
* @return the dummy state.
*/
State InitialSample() { return State(); }
/**
* Dummy function to find terminal state.
*
* @param * (state) The current state.
* @return It's of no use but so lets keep it false.
*/
bool IsTerminal(const State& /* state */) const { return false; }
};
size_t DiscreteActionEnv::State::dimension = 0;
size_t DiscreteActionEnv::Action::size = 0;
k 臂赌博机
#ifndef K_ARMED_BANDITS_HPP
#define K_ARMED_BANDITS_HPP
#include <random>
#include <mlpack/methods/reinforcement_learning/environment/env_type.hpp>
const size_t K = 10;
class K_armed_Bandits : public mlpack::rl::DiscreteActionEnv
{
public:
class Action : public DiscreteActionEnv::Action
{
public:
static const size_t size = K;
};
K_armed_Bandits()
: rd{}
, rng{rd()}
, norm{}
{ }
double Sample(const Action& action)
{
using Params = std::normal_distribution<>::param_type;
double mu = static_cast<double>(action.action);
double sigma {2.0};
Params newParam {mu, sigma};
return norm(rng, newParam);
}
private:
std::random_device rd;
std::knuth_b rng;
std::normal_distribution<> norm;
};
#endif // K_ARMED_BANDITS_HPP
这里简单起见,我们设置
k
=
10
k=10
k=10 ,即为 10 臂赌博机
其中,选择拉杆
i
i
i 收到的数值奖励服从数学期望为
i
i
i ,标准差为 2.0 的正态分布
策略
ε varepsilon ε 贪婪
/**
* Implementation for epsilon greedy policy.
*
* In general we will select an action greedily based on the action value,
* however sometimes we will also randomly select an action to encourage
* exploration.
*
* @tparam EnvironmentType The reinforcement learning task.
*/
template <typename EnvironmentType>
class GreedyPolicy
{
public:
//! Convenient typedef for action.
using ActionType = typename EnvironmentType::Action;
/**
* Constructor for epsilon greedy policy class.
*
* @param initialEpsilon The initial probability to explore
* (select a random action).
* @param annealInterval The steps during which the probability to explore
* will anneal.
* @param minEpsilon Epsilon will never be less than this value.
* @param decayRate How much to change the model in response to the
* estimated error each time the model weights are updated.
*/
GreedyPolicy(const double initialEpsilon,
const size_t annealInterval,
const double minEpsilon,
const double decayRate = 1.0) :
epsilon(initialEpsilon),
minEpsilon(minEpsilon),
delta(((initialEpsilon - minEpsilon) * decayRate) / annealInterval)
{ /* Nothing to do here. */ }
/**
* Sample an action based on given action values.
*
* @param actionValue Values for each action.
* @param deterministic Always select the action greedily.
* @param isNoisy Specifies whether the network used is noisy.
* @return Sampled action.
*/
ActionType Sample(const arma::colvec& actionValue,
bool deterministic = false,
const bool isNoisy = false)
{
double exploration = math::Random();
ActionType action;
// Select the action randomly.
if (!deterministic && exploration < epsilon && isNoisy == false)
{
action.action = static_cast<decltype(action.action)>
(math::RandInt(ActionType::size));
}
// Select the action greedily.
else
{
action.action = static_cast<decltype(action.action)>(
arma::as_scalar(arma::find(actionValue == actionValue.max(), 1)));
}
return action;
}
/**
* Exploration probability will anneal at each step.
*/
void Anneal()
{
epsilon -= delta;
epsilon = std::max(minEpsilon, epsilon);
}
/**
* @return Current possibility to explore.
*/
const double& Epsilon() const { return epsilon; }
private:
//! Locally-stored probability to explore.
double epsilon;
//! Locally-stored lower bound for epsilon.
double minEpsilon;
//! Locally-stored stride for epsilon to anneal.
double delta;
};
完全贪婪的行为是目光短浅的,它总是在利用已有的知识来最大化立即收益,从不尝试目前来说较弱,但也许会是更好的行为。因此,我们做出改进,在采样时,以较小的概率 ε varepsilon ε 放下已有成见,一视同仁的在行为空间中进行采样。
不过,当我们对几乎所有的行为做了足够多的尝试后,已有的知识也越来越来丰富,继续探索的必要性也越来越小
这两个过程分别对应程序里的 Sample (采样)和 Anneal (退火)
记 initialEpsilon 为
ε
0
varepsilon_0
ε0 ,annealInterval 为
T
T
T ,minEpsilon 为
ε
m
i
n
varepsilon_{min}
εmin ,decayRate 为
α
alpha
α
退火过程中,
ε
t
varepsilon_t
εt 的更新过程为:
δ
=
α
⋅
(
ε
0
−
ε
m
i
n
)
T
ε
t
+
1
=
max
(
ε
m
i
n
,
ε
t
−
δ
)
delta = dfrac{alpha cdot (varepsilon_0 - varepsilon_{min})}{T} \[5pt] varepsilon_{t+1} = max (varepsilon_{min} , varepsilon_t - delta)
δ=Tα⋅(ε0−εmin)εt+1=max(εmin , εt−δ)
UCB
ε varepsilon ε 贪婪策略在进行 “不贪婪” 的行动时,不能简单的 “一视同仁” ,最好是根据它们实际具有的成为最优的潜力来考量,也就是说,我们要将对它们的估计与最大值的接近程度以及估计中的不确定性也纳入考虑范围。
按照《Reinforcement Learning An Introduction》(second edition) 书中的提示,一种选择方法是:
A
t
≐
arg max
a
[
Q
t
(
a
)
+
c
ln
t
N
t
(
a
)
]
A_t doteq argmax_a left[ Q_t(a) + c sqrt{dfrac{ln t}{N_t(a)}} right]
At≐aargmax[ Qt(a)+cNt(a)lnt ]
实现:
#ifndef EPSILONGREEDY_HPP
#define EPSILONGREEDY_HPP
#include <algorithm>
#include <mlpack/core.hpp>
#include <mlpack/prereqs.hpp>
#include <mlpack/methods/reinforcement_learning/policy/greedy_policy.hpp>
#include "K_armed_Bandits.hpp"
class UCB_Greedy : public mlpack::rl::GreedyPolicy<K_armed_Bandits>
{
public:
UCB_Greedy(double initialEpsilon,
const size_t annealInterval,
const double minEpsilon,
const double decayRate,
const double c = 2.0)
: GreedyPolicy(initialEpsilon, annealInterval, minEpsilon, decayRate)
, c_(c) { }
ActionType Sample(const arma::colvec& actionValue,
const arma::colvec& actionNum,
const size_t t)
{
double exploration = mlpack::math::Random();
ActionType action;
if (t == 0) {
action.action = static_cast<decltype (action.action)>(
(mlpack::math::RandInt(ActionType::size)));
} else {
// Select the action randomly according to UCB
if (exploration < Epsilon()) {
std::vector<double> tmp(actionValue.n_elem);
for (size_t i = 0; i < tmp.size(); ++i) {
if (actionNum[i] == 0)
tmp[i] = std::numeric_limits<double>::infinity();
else
tmp[i] = actionValue[i] + c_ * std::sqrt(std::log(t) / actionNum[i]);
}
action.action = static_cast<decltype (action.action)>(
std::max_element(tmp.cbegin(), tmp.cend()) - tmp.cbegin());
}
// Select the action greedily
else {
action.action = static_cast<decltype (action.action)>(
arma::as_scalar(arma::find(actionValue == actionValue.max(), 1)));
}
}
return action;
}
private:
const double c_;
};
#endif // EPSILONGREEDY_HPP
实验
我们使用《Reinforcement Learning An Introduction》 书中介绍的简单赌博机算法:

实现如下:
#include <iostream>
#include "K_armed_Bandits.hpp"
#include "EpsilonGreedy.hpp"
using namespace std;
using namespace arma;
using namespace mlpack::rl;
extern const size_t K;
int main()
{
const double initialEpsilon = 1.0;
const size_t annealInterval = 10;
const double minEpsilon = 0.01;
const double decayRate = 0.99;
size_t maxIterations = 2000;
K_armed_Bandits bandits;
GreedyPolicy<K_armed_Bandits> greedy(initialEpsilon,
annealInterval,
minEpsilon,
decayRate);
UCB_Greedy ucbGreedy(initialEpsilon,
annealInterval,
minEpsilon,
decayRate);
colvec actionValue_1(K);
colvec actionValue_2(K);
colvec actionNum_1(K);
colvec actionNum_2(K);
double total_1 {};
double total_2 {};
for (size_t i = 0; i < maxIterations; ++i) {
auto greedyAction = greedy.Sample(actionValue_1);
auto ucbAction = ucbGreedy.Sample(actionValue_2, actionNum_2, i);
double reward_1 = bandits.Sample(greedyAction);
double reward_2 = bandits.Sample(ucbAction);
total_1 += reward_1;
total_2 += reward_2;
++actionNum_1[greedyAction.action];
++actionNum_2[ucbAction.action];
actionValue_1[greedyAction.action] += (reward_1 - actionValue_1[greedyAction.action])
/ (actionNum_1[greedyAction.action]);
actionValue_2[ucbAction.action] += (reward_2 - actionValue_2[ucbAction.action])
/ (actionNum_2[ucbAction.action]);
}
cout << "action value 1:n"
<< actionValue_1 << endl;
cout << "action value 2:n"
<< actionValue_2 << endl;
cout << "greedy total reward:n"
<< total_1 << endl;
cout << "ucb total reward:n"
<< total_2 << endl;
}
输出:
| action value 1 | action value 2 |
|---|---|
| -0.1154 | 0.4100 |
| 1.1166 | 2.4985 |
| 1.7982 | 4.5769 |
| 3.0406 | 2.6635 |
| 4.0761 | 0.1001 |
| 5.0469 | 5.2899 |
| 5.8544 | 4.9228 |
| 6.7210 | 6.1781 |
| 7.9360 | 7.6092 |
| 8.8647 | 8.9199 |
| greedy total reward | ucb total reward |
|---|---|
| 8858.03 | 17746.3 |
可以看到,两者都找到了正确的价值函数,但因为我们并没有退火,因此,greedy 策略实际上是个随机策略,它的总回报也显得很可怜;而由于 ucb 在随机选择时考虑到了 actionValue 的值,因此表现较好
这只是显示一下随机策略的后果,下面是 greedy 和 ucb 的正式较量:
#include <iostream>
#include "K_armed_Bandits.hpp"
#include "EpsilonGreedy.hpp"
using namespace std;
using namespace arma;
using namespace mlpack::rl;
extern const size_t K;
int main()
{
const double initialEpsilon = 1.0;
const size_t annealInterval = 10;
const double minEpsilon = 0.01;
const double decayRate = 0.99;
K_armed_Bandits bandits;
GreedyPolicy<K_armed_Bandits> greedy(initialEpsilon,
annealInterval,
minEpsilon,
decayRate);
UCB_Greedy ucbGreedy(initialEpsilon,
annealInterval,
minEpsilon,
decayRate);
vector<double> total_1;
vector<double> total_2;
for (size_t maxIterations = 100; maxIterations <= 10000; maxIterations += 100) {
double tmp_1 { };
double tmp_2 { };
for (size_t t = 0; t < 5; ++t) {
colvec actionValue_1(K);
colvec actionValue_2(K);
colvec actionNum_1(K);
colvec actionNum_2(K);
for (size_t i = 0; i < maxIterations; ++i) {
auto greedyAction = greedy.Sample(actionValue_1);
auto ucbAction = ucbGreedy.Sample(actionValue_2, actionNum_2, i);
double reward_1 = bandits.Sample(greedyAction);
double reward_2 = bandits.Sample(ucbAction);
tmp_1 += reward_1;
tmp_2 += reward_2;
++actionNum_1[greedyAction.action];
++actionNum_2[ucbAction.action];
actionValue_1[greedyAction.action] += (reward_1 - actionValue_1[greedyAction.action])
/ (actionNum_1[greedyAction.action]);
actionValue_2[ucbAction.action] += (reward_2 - actionValue_2[ucbAction.action])
/ (actionNum_2[ucbAction.action]);
if (i % (maxIterations / annealInterval) == 0) {
greedy.Anneal();
ucbGreedy.Anneal();
}
}
}
total_1.push_back(tmp_1 / 5);
total_2.push_back(tmp_2 / 5);
}
for (auto i : total_1)
cout << i << ", ";
cout << endl;
for (auto i : total_2)
cout << i << ", ";
}
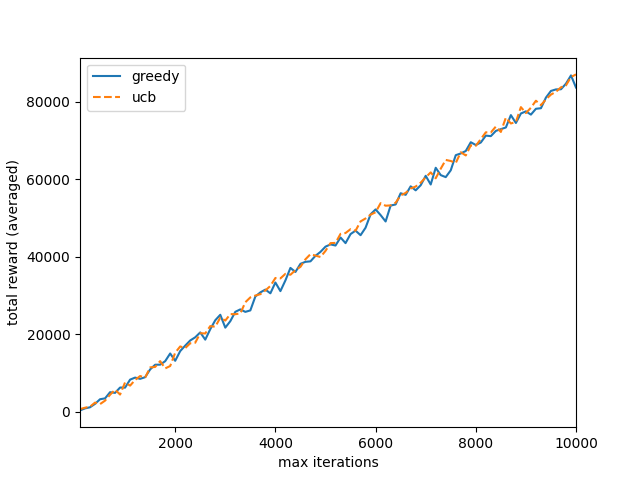
可视化后的结果:
参考
《Reinforcement Learning An Introduction》(second edition)
mlpack rl
最后
以上就是深情棒球最近收集整理的关于K-armed Bandit环境策略实验参考的全部内容,更多相关K-armed内容请搜索靠谱客的其他文章。








发表评论 取消回复