对“一棵有124个叶节点的完全二叉树，最多有多少个结点”的思考

在网上看到这个问题，在讨论答案到底是248，还是247，评论普遍认为是247，但我觉得答案是248

先再读一遍题目，里面有“最多”两个字，也就是说能满足条件的完全二叉树不止一种，要找出结点最多的那个

评论里的人几乎都认为答案唯一且为247，评论里的观点是：非叶节点数目 = 叶节点-1

这个观点并不是完全正确的，它需要加上一个前提，就是完全二叉树的最右非终结结点的子树个数是二

下面我按照最右非终结结点的子树是二和一两种情况进行分析：

一、最右非终结结点的子树个数是二

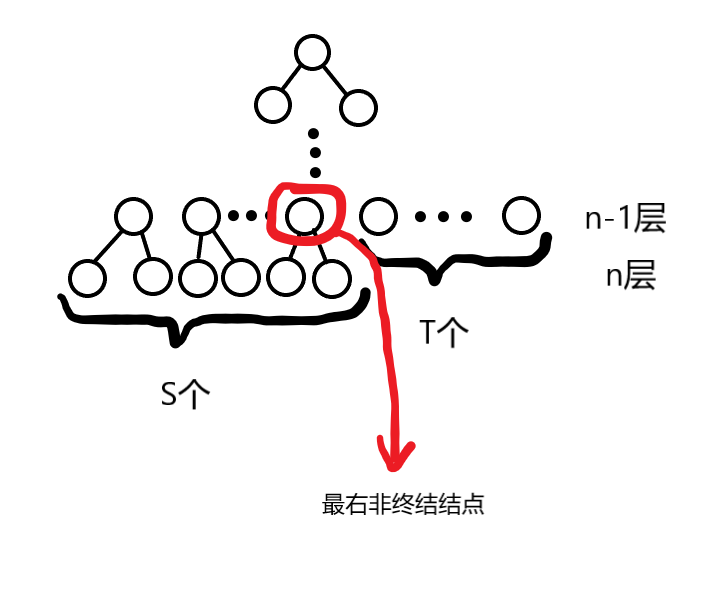
除去第n层的全部结点数：$2^{n-1}-1$

总结点数：$2^{n-1}-1+S$
由此，可以得到:非叶节点数 = 总结点数 $-S-T$ = $2^{n-1}-T-1$——————1

第n-1层结点数：$S/2+T$ 或 $2^{n-2}$
由此，得到等式：$S/2+T=2^{n-2}$
将等式变型得到：叶结点数=$S+T=2^{n-1}-T$——————————————2

将1,2两式联立(将最后得到的数值进行比较)，得：非叶节点数目 = 叶节点-1

二、最右非终结结点的子树个数是一

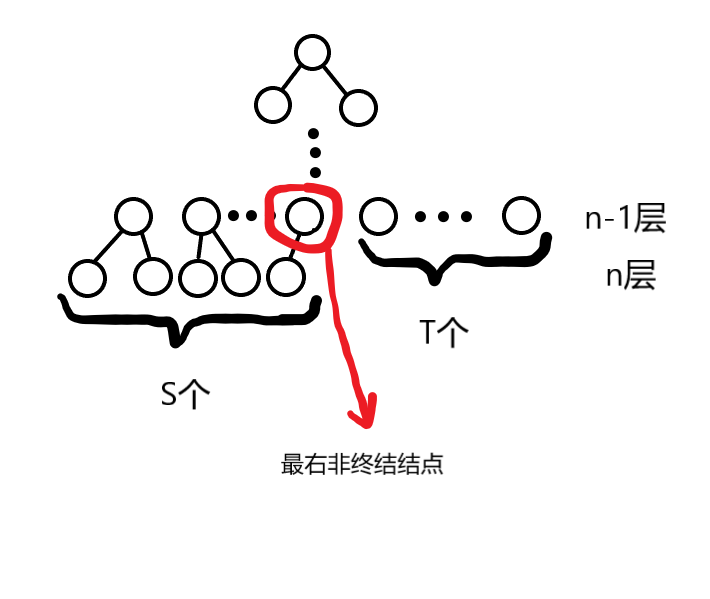
除去第n层的全部结点数：$2^{n-1}-1$

总结点数：$2^{n-1}-1+S$
由此，可以得到:非叶节点数 = 总结点数 $-S-T$ = $2^{n-1}-T-1$——————1

第n-1层结点数：$（S+1）/2+T$ 或 $2^{n-2}$
由此，得到等式：$（S+1）/2+T=2^{n-2}$
将等式变型得到：叶结点数=$S+T$=$2^{n-1}-T-1$————————————2

将1,2两式联立(将最后得到的数值进行比较)，得：非叶节点数目 = 叶节点

最终结论：
当完全二叉树的最右非终结结点子树个数为一时，非叶节点数目 = 叶节点；
当完全二叉树的最右非终结结点子树个数为二时，非叶节点数目 = 叶节点-1

所以，再回到题目本身，我们也要分两种情况讨论：
1.最右非终结结点子树个数为二时，非叶结点数$=124-1=123$
二叉树结点总数$=124+123=247$
$S=120,T=4$ (相加后就是题目要求的叶节点的总数，S和T不清楚的再看一下上面的图)
第n-1层结点数量为：$64$（即$S/2+T$）
$64$是$2^6$,符合完全二叉树的特点

2.最右非终结结点子树个数为一时，非叶结点数$=124$
二叉树结点总数$=124+124=248$
$S=121,T=3$ (相加后就是题目要求的叶节点的总数)
第n-1层结点数量为：$64$（即$(S+1)/2+T$）
$64$是$2^6$,符合完全二叉树的特点

又因为题目要求最大总结点数，取第二种情况，答案：$248$

不好意思，之前由于本人的疏忽，本题的结论有一些错误，推导过程没有问题，现已修改过来，对于给大家理解时带来的误导和不便十分抱歉。
感谢zonezn指出本文结论中的错误！

最后

以上就是饱满大象为你收集整理的对“一棵有124个叶节点的完全二叉树，最多有多少个结点”的思考的全部内容，希望文章能够帮你解决对“一棵有124个叶节点的完全二叉树，最多有多少个结点”的思考所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。