实现二叉树中度为0、1、2的结点总数，实现二叉树的深度、创建二叉树

63 阅读 0 评论 42 点赞

我是靠谱客的博主轻松小蜜蜂，最近开发中收集的这篇文章主要介绍实现二叉树中度为0、1、2的结点总数，实现二叉树的深度、创建二叉树，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

此文章主要是实现之前两篇文章中涉及的关于二叉树的一些算法、之前零散的算法知识难以将二叉树的一些知识算法贯穿起来，通过简单实现二叉树有助于理解算法含义、加深印象

之前的算法描述请看：
计算二叉树中度为0、1、2的结点个数、深度、结点总数、二叉树的复制等算法
二叉树的先、中、后三种遍历

下面是算法实现结果
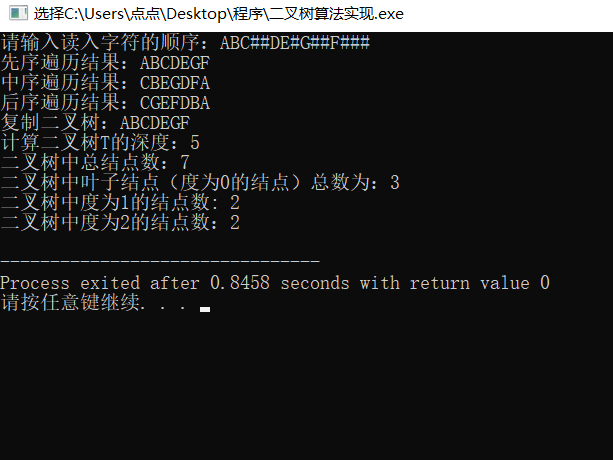
在这里插入图片描述

具体代码如下：

#include<iostream>
using namespace std;
typedef struct BiTNode{
	 char data;
	 struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

//先序遍历创建二叉树
void CreateBiTree(BiTree &T)
{
	 char ch; 
	 cin>>ch;
	 if(ch=='#')
	  T=NULL;
	 else
	 {
		  T=new BiTNode;//生成根结点
		  T->data=ch;//将根结点数据域置为ch
		  CreateBiTree(T->lchild);//递归创建左子树
		  CreateBiTree(T->rchild);//递归创建右子树
	 }//如果不用void 类型，必须写返回值，如return OK,return true等
	}//CreateBiTree 
	
//先序遍历
void PreOrderTraverse(BiTree T)
{
	 if(T==NULL)
	  return ;
	 else
	  {
	   cout<<T->data;
	   PreOrderTraverse(T->lchild);
	   PreOrderTraverse(T->rchild);
 	  } 
 } 
//中序遍历
void InOrderTraverse(BiTree T)
{
	 if(T==NULL)
	  return;
	 else
	 {
	 	 InOrderTraverse(T->lchild);
 		 cout <<T->data;
  		 InOrderTraverse(T->rchild);
 }
}

//后序遍历
void PostOrderTraverse(BiTree T)
{
	 if(T==NULL)
	  return;
	 else
	 {
	  PostOrderTraverse(T->lchild);
	  PostOrderTraverse(T->rchild);
	  cout <<T->data;
	 }
}
	
//复制二叉树
int Copy(BiTree T,BiTree &NewT)
{
	 if(T==NULL)//如果是空树，递归结束
	 {
	  NewT=NULL;
	  return 0;
	 }
	 else
	 {
		  NewT=new BiTNode;
		  NewT->data=T->data;//复制根结点
		  Copy(T->lchild,NewT->lchild);//递归复制左子树
		  Copy(T->rchild,NewT->rchild);//递归复制右子树
	}	  
 }

//计算二叉树的深度 
int Depth(BiTree T)
{
	 int m,n;
	 if(T==NULL)
	  return 0;//如果是空树,返回深度0，递归结束
	 else
	 {
		  m=Depth(T->lchild);//递归计算左子树深度记为m
		  n=Depth(T->rchild);//递归计算右子树的深度记为n
		  if(m>n)
			 return (m+1);
		  else
		   return (n+1); 
		 }// 二叉树的深度为m与n的较大者+1
		}
		
//计算二叉树结点总数
int NodeCount(BiTree T)
{
	 if(T==NULL)
	  return 0;
	 else
	  return NodeCount(T->lchild)+NodeCount(T->rchild)+1; 
}

// 计算二叉树 叶子结点（度为0）总数 
int LeafCount(BiTree T)
{
	 if(T==NULL)//如果树为空返回0
	  return 0;
	 if(T->lchild==NULL && T->rchild==NULL)
	  return 1;//如果是叶子结点返回1 
	 else
	  return  LeafCount(T->lchild)+LeafCount(T->rchild);
}//叶子结点总数

//度为1的结点个数 
int oneCount(BiTree T)
{
	 int i=0;
	 if(T==NULL)//如果树为空返回0
	  return 0;
	  if((T->lchild!=NULL&&T->rchild==NULL)||(T->lchild==NULL&&T->rchild!=NULL))
	  return 1+oneCount(T->lchild)+oneCount(T->rchild); 
	  else 
	  return oneCount(T->lchild)+oneCount(T->rchild);
}

//度为2的结点个数
 int twoCount(BiTree T)
{
	 int i=0;
	 if(T==NULL)//如果树为空返回0
	  return 0;
	if(T->lchild!=NULL && T->rchild!=NULL)
	  return 1+twoCount(T->lchild)+twoCount(T->rchild); 
	 else 
	  return twoCount(T->lchild)+twoCount(T->rchild);
}

int main()
{
	 BiTree T,F;
	 
	 cout<<"请输入读入字符的顺序：";
	 //测试用例：ABC##DE#G##F###
	 CreateBiTree(T);
	
	 cout<<"先序遍历结果：";
	 PreOrderTraverse(T);
	 cout<<endl;
	 
	 cout<<"中序遍历结果：";
	 InOrderTraverse(T);
	 cout<<endl;
	 
	 cout<<"后序遍历结果：";
	 PostOrderTraverse(T);
	 cout<<endl;
	 
	 cout<<"复制二叉树：";
	 Copy(T,F);
	 PreOrderTraverse(F);//前序遍历 
	 cout<<endl;
	 
	 cout<<"计算二叉树T的深度：";
	 cout<<Depth(T)<<endl;
	 
	 cout<<"二叉树中总结点数：";
	 cout<<NodeCount(T)<<endl;
	 
	 cout<<"二叉树中叶子结点（度为0的结点）总数为：";
	 cout<<LeafCount(T)<<endl;
	 
	 cout<<"二叉树中度为1的结点数: "; 
	 cout<<oneCount(T)<<endl;
	 
	 cout<<"二叉树中度为2的结点数：";
	 cout<<twoCount(T)<<endl; 
	 return 0;
}