概述
https://iai.sh.cn/contest/44
3h.
第一次提交：320pts。比赛结束前：400pts。
比赛期间 第一次提交
先把四道题都读了一遍，感觉这次比较简单。顺着做吧。
此时3min。
T1 数对统计
贪心 - AC
数对(x,y)，x已知，选等于x的数中最左边的那个，数y。
此时10min。
int n, a[MAXN], pos[MAXN];
ll cnt, ans;
bool vh[MAXN];
int main() {
// ios::sync_with_stdio(false);
// cin.tie(nullptr); cout.tie(nullptr);
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d", a + i);
if (!pos[a[i]]) pos[a[i]] = i;
}
for (int i = n; i; --i) {
if (i == pos[a[i]]) ans += cnt;
if (!vh[a[i]]) ++cnt;
vh[a[i]] = true;
}
printf("%lldn", ans);
return 0;
}
T2 序列操作
暴力之前
以前好像做过，但是完全忘了。
诚然，线段树可做。但是，对这个单点加法，全部乘法来说，有点大材小用了。
对于某个位置的数，它等于
m
3
(
m
2
(
m
1
x
+
q
1
)
+
q
2
)
+
q
3
m_3(m_2(m_1x+q_1)+q_2)+q_3
m3(m2(m1x+q1)+q2)+q3，这里只是举个例子。对于不同的数，几个m和q是不同的。
借鉴懒标记。我想，是不是要弄个乘法懒标记？但是在一个数上做加法，要修改整个懒标记，别的数不变，不好做。
我接着想到把它变成
m
1
m
2
m
3
(
m
1
−
1
(
m
2
−
1
(
m
3
−
1
q
3
+
q
2
)
+
q
1
)
+
x
)
m_1m_2m_3(m_1^{-1}(m_2^{-1}(m_3^{-1}q_3+q_2)+q_1)+x)
m1m2m3(m1−1(m2−1(m3−1q3+q2)+q1)+x)，用乘法逆元做。但是，输入是1 2 3的顺序，这里的运算顺序却是3 2 1。还是不好做。
先打个暴力吧，再看看后面的题。
此时25min。
暴力 - 没交
此时30min。
int n, q;
ll a[MAXN];
int main() {
// ios::sync_with_stdio(false);
// cin.tie(nullptr); cout.tie(nullptr);
cin >> n >> q;
while (q--) {
char ch; cin >> ch;
int p; ll d;
if (ch == '+') {
cin >> p >> d;
plusmod(a[p], d);
}
else {
cin >> d;
for (int i = 1; i <= n; ++i) a[i] = mod(a[i] * d);
}
}
for (int i = 1; i <= n; ++i) {
cout << a[i] << " ";
} cout << "n";
return 0;
}
T3 菜单设计
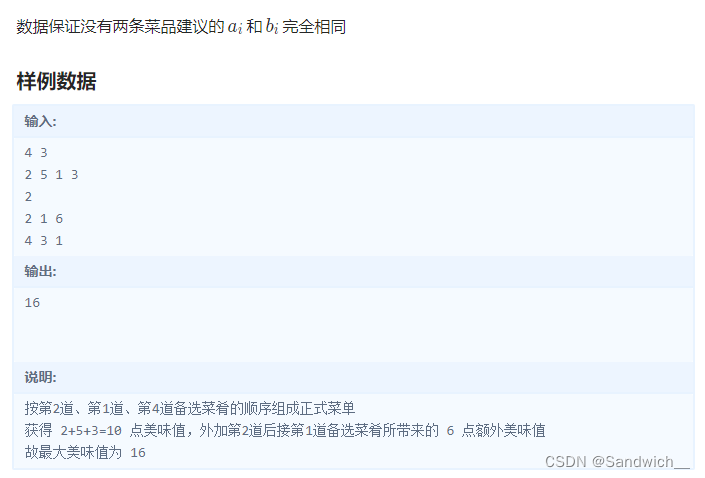
状压dp - 20pts WA
不讲。
此时45min，慢了，状态设计一开始没想清楚。
int n, m, p;
ll x[MAXN], c[MAXN][MAXN], dp[MAXSTA][MAXN], ans;
int popcnt(int x) {
int res = 0;
while (x) x &= (x - 1), ++res;
return res;
}
int main() {
// ios::sync_with_stdio(false);
// cin.tie(nullptr); cout.tie(nullptr);
scanf("%d%d", &n, &m);
for (int i = 0; i < n; ++i) {
scanf("%lld", x + i);
}
scanf("%d", &p);
for (int i = 1; i <= p; ++i) {
int a, b; scanf("%d%d", &a, &b);
scanf("%lld", &c[a - 1][b - 1]);
}
for (int s = 1; s < (1 << n); ++s) {
int cnt = popcnt(s);
if (cnt <= m) {
for (int i = 0; i < n; ++i) {
int v = s ^ (1 << i);
if (v < s) {
for (int j = 0; j < n; ++j) {
ckmax(dp[s][i], dp[v][j] + x[i] + c[j][i]);
}
}
if (cnt == m) ckmax(ans, dp[s][i]);
}
}
}
printf("%lldn", ans);
return 0;
}
T4 树的链接
并查集、LCA、离线算法 - AC
不难发现，过程中一直是森林或树。（“树的链接”疯狂暗示）
询问两点间最短路，其实最多只能找到一条简单路径。过程中某两个点间如果有路径了，再怎么加边，都不会影响这条路径。
先不考虑询问，把建的边全部读一遍，建一个树。
再把询问都用LCA算一遍答案。当然，在询问时，两个点可能还没有连通。所以用并查集看一下，如果连通了，答案就是最后的树上的路径长度，否则-1。
另外，最后可能不是一个树，而是一个森林，不方便计算答案。可以加几条边，把它变成一个树，反正不影响答案，并查集会检测的。
另外，这题的输入。每一行，要么两个数，要么三个数。
一开始我借助字符串输入。先读一整行，然后看有几个数，每个数都用字符串读入。这样很麻烦，我还写错了。
于是我想到先直接读两个int进来，简单。再用字符串把这一行剩下的东西读进来。
此时1h30min。lca和并查集我是边写边调试，如果下次能一次性写出来，应该能节省一些时间。
struct Edge {
int v, w;
Edge(int _v = 0, int _w = 0): v(_v), w(_w){}
};
struct Node {
int t, x, y;
} a[MAXN];
int n, q, st[MAXN], fa[MAXN][MAXP], dep[MAXN], dis[MAXN];
vector<Edge> g[MAXN];
int find(int x) {
return st[x] == x ? x : st[x] = find(st[x]);
}
void merge(int x, int y) {
st[find(x)] = find(y);
}
void predfs(int u, int par) {
dep[u] = dep[par] + 1;
fa[u][0] = par;
for (int i = 1; i < MAXP; ++i) {
fa[u][i] = fa[fa[u][i - 1]][i - 1];
}
for (int i = 0; i < g[u].size(); ++i) {
int v = g[u][i].v, w = g[u][i].w;
if (v == par) continue;
dis[v] = dis[u] + w;
predfs(v, u);
}
}
int lca(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
int d = dep[x] - dep[y];
for (int i = 0; i < MAXP; ++i) {
if (d & (1 << i)) x = fa[x][i];
}
if (x == y) return x;
for (int i = MAXP - 1; i >= 0; --i) {
if (fa[x][i] != fa[y][i]) {
x = fa[x][i]; y = fa[y][i];
}
}
return fa[x][0];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
cin >> n >> q;
for (int i = 1; i <= n; ++i) st[i] = i;
for (int i = 1; i <= q; ++i) {
cin >> a[i].x >> a[i].y;
string s; getline(cin, s);
if (s.size()) {
int w = 0;
for (int j = 1; j < s.size(); ++j) w = w * 10 + (s[j] - '0');
a[i].t = 1;
g[a[i].x].push_back(Edge(a[i].y, w));
g[a[i].y].push_back(Edge(a[i].x, w));
merge(a[i].x, a[i].y);
}
else {
a[i].t = 0;
}
}
for (int i = 2; i <= n; ++i) {
if (find(i) != find(1)) {
g[i].push_back(Edge(1, 1));
g[1].push_back(Edge(i, 1));
merge(i, 1);
}
}
predfs(1, 0);
for (int i = 1; i <= n; ++i) st[i] = i;
for (int i = 1; i <= q; ++i) {
int x = a[i].x, y = a[i].y;
if (!a[i].t) {
int anc = lca(x, y);
int res = dis[x] + dis[y] - 2 * dis[anc];
if (find(x) == find(y)) printf("%dn", res);
else printf("-1n");
}
else {
merge(x, y);
}
}
return 0;
}
T2 序列操作
回到这里。
倒着算 - AC
我依旧对刚刚的
m
1
m
2
m
3
(
m
1
−
1
(
m
2
−
1
(
m
3
−
1
q
3
+
q
2
)
+
q
1
)
+
x
)
m_1m_2m_3(m_1^{-1}(m_2^{-1}(m_3^{-1}q_3+q_2)+q_1)+x)
m1m2m3(m1−1(m2−1(m3−1q3+q2)+q1)+x)抱有执念。
可是这个3 2 1的顺序还是很烦啊！
……等等。
顺序？
尝试从外向内看一下
m
3
(
m
2
(
m
1
x
+
q
1
)
+
q
2
)
+
q
3
m_3(m_2(m_1x+q_1)+q_2)+q_3
m3(m2(m1x+q1)+q2)+q3。
此时，这题就结束了。
此时1h50min。
struct Node {
int t, p; ll d;
} op[MAXQ];
int n, q;
ll a[MAXN], mul;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
cin >> n >> q;
for (int i = 1; i <= q; ++i) {
char ch; cin >> ch;
if (ch == '+') {
op[i].t = 0;
cin >> op[i].p >> op[i].d;
}
else {
op[i].t = 1;
cin >> op[i].d;
}
}
mul = 1;
for (int i = q; i; --i) {
if (op[i].t) {
mul = mod(mul * op[i].d);
}
else {
plusmod(a[op[i].p], mod(mul * op[i].d));
}
}
for (int i = 1; i <= n; ++i) {
cout << a[i] << " ";
} cout << "n";
return 0;
}
对拍
还有一个多小时，对拍玩。
对拍过了，放心交。
此时2h。
比赛期间 比赛结束前
T3 菜单设计
状压dp - AC
当时20pts WA。
一个小错误：
for (int s = 1; s < (1 << n); ++s) {
int cnt = popcnt(s);
if (cnt <= m) {
for (int i = 0; i < n; ++i) {
int v = s ^ (1 << i);
if (v < s) {
for (int j = 0; j < n; ++j) {
ckmax(dp[s][i], dp[v][j] + x[i] + c[j][i]);//这里
}
}
if (cnt == m) ckmax(ans, dp[s][i]);
}
}
}
当cnt=1时，在“这里”，会凭空加一个
c
[
j
]
[
i
]
>
0
c[j][i]>0
c[j][i]>0。
改成这样就过了：
ckmax(dp[s][i], dp[v][j] + x[i] + c[j][i] * (cnt > 1));
使用__builtin_popcount()
如题。
最后
以上就是犹豫曲奇为你收集整理的上海市计算机学会竞赛平台2022年11月月赛乙组 总结比赛期间 第一次提交比赛期间 比赛结束前的全部内容，希望文章能够帮你解决上海市计算机学会竞赛平台2022年11月月赛乙组 总结比赛期间 第一次提交比赛期间 比赛结束前所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复