动态规划学习总结
首先想要学好动态规划最重要的就是了解什么是动态规划,动态规划是用来求解以时间划分阶段的动态过程的优化问题,就是把一个问题分为若干个阶段,即分为若干个小问题,然后逐个求解的过程
在Vjudge的课程作业中我找到了两个不同的类型的动态规划题型,感觉比较具有代表性(作业地址https://vjudge.net/contest/430905)
类型1,其实就是求最大连续增长序列的最大值,包含题目:C,U(其实U就是简化版的C)
思想:这种题型就是求最大连续增长序列和的最大值的问题,比如一组数1,3,2最大的连续增长序列和的最大值为3,可以是3自己,也可以是1和2的和值,首先根据动态规划原则,将问题分为一个个的小问题,依次求解,这里就是从第一个数开始,依次求以该位置为末尾的最大值,这里dp只需要用一维数组即可解决问题,不过需要使用二重循环,dp[i]的初值为a[i]本身
主要代码如下:
for(i=2;i<=n;i++)
{
dp[i]=a[i];
for(int j=1;j<=i;j++){
if(a[i]>a[j]){
if(dp[j]+a[i]>dp[i])
dp[i]=dp[j]+a[i];
}
}
m=max(m,dp[i]);
}
从第一个值i开始,一次进行第一重循环,第二重循环的位置j从第一个数开始到第一重循环开始的位置结束,那么,为什么要这么做?因为当在求以第i个数为结尾的最大值时,需要判断与前面的任何一个数的关系,如果满足递增,即a[i]>a[j]成立,再判断j位置最大值加上i位置的值是否大于i位置的最大值(即与之前位置判断结果的大小进行比较),如果成立就执行 dp[i]=dp[j]+a[i];改变i位置的最大值,在每一重第一重循环结束的时候取最大值m=max(m,dp[i]);最后m即所求结果
U:
思路为基本思路,按照该类型的思路求解即可AC,AC代码如下:
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
int dp[1010];
int main()
{
int a[1010],n;
while(cin>>n&&n!=0)
{
memset(dp,0,sizeof(dp));
int i,m=0;
for(i=1;i<=n;i++)
cin>>a[i];
dp[1]=a[1];
for(i=2;i<=n;i++)
{
dp[i]=a[i];
for(int j=1;j<=i;j++){
if(a[i]>a[j]){
if(dp[j]+a[i]>dp[i])
dp[i]=dp[j]+a[i];
}
}
m=max(m,dp[i]);
}
cout<<m<<endl;
}
}
C(加强版的U题):
思路:跟U比起来其实就是需要排序,然后多了一个输出位置的要求,首先排序需要按照小鼠的重量进行排序,输入的时候需要记录下每个小数的原始位置
while(cin>>m[t].w>>m[t].s)
{
m[t].n=t;
t++;
}
这时候使用结构体变量就比较方便,排序只需要排重量即可,排序代码如下(sort函数)
bool cmp(mice a,mice b)
{
if(a.w!=b.w)
return a.w<b.w;
}
接下来就是类型题目的标准代码:
for(i=1;i<=t;i++)
{
p[i]=i;
dp[i]=1;
for(j=1;j<i;j++)
{
if(m[i].w!=m[j].w&&m[i].s<m[j].s)
{
if(dp[i]<dp[j]+1)
{
p[i]=j;
dp[i]=dp[j]+1;
}
}
}
}
这里的数组p表示以i为结尾的最大值时,i的上一个位置,用来求解各个位置(temp为排序后的末尾最大值的位置)
i=0;
while(p[temp]!=temp)//到末尾最大值的上一个位置是自己本身时,结束判断语句
{
postion[i]=m[temp].n;//得出原始位置
temp=p[temp];//末尾最大值的位置往前推1
i++;
}
如果最大值本身不是自己,运行语句,postion[i]表示排序前的各个位置,最后输出
cout<<m[temp].n<<endl;
for(j=i-1;j>=0;j--)
cout<<postion[j]<<endl;
AC代码如下:
#include <iostream>
#include <algorithm>
#include <string.h>
#include <stdio.h>
using namespace std;
struct mice
{
int w,s,n;
}m[1005];
int dp[1005]={0},p[1005]={0};//以i结尾最大数值
bool cmp(mice a,mice b)
{
if(a.w!=b.w)
return a.w<b.w;
}
int main()
{
int t=1;
while(cin>>m[t].w>>m[t].s)
{
m[t].n=t;
t++;
}
sort(m+1,m+1+t,cmp);
t--;
memset(dp,0,sizeof(dp));
int i,j;
for(i=1;i<=t;i++)
{
p[i]=i;
dp[i]=1;
for(j=1;j<i;j++)
{
if(m[i].w!=m[j].w&&m[i].s<m[j].s)
{
if(dp[i]<dp[j]+1)
{
p[i]=j;
dp[i]=dp[j]+1;
}
}
}
}
int maxx=0,temp=0;
for(i=1;i<=t;i++)
{
if(dp[i]>maxx)
{
maxx=dp[i];
temp=i;
}
}
cout<<maxx<<endl;
int postion[10010]={0};
i=0;
while(p[temp]!=temp)
{
postion[i]=m[temp].n;
temp=p[temp];
i++;
}
cout<<m[temp].n<<endl;
for(j=i-1;j>=0;j--)
cout<<postion[j]<<endl;
return 0;
}
类型2,一个问题有两种状态,包含题目:A,D,M,R
思想:包含两个状态,从这两个状态入手,其实就是直接或间接求出相对应两个状态的值最后进行比较,可以根据下面图片进行dp
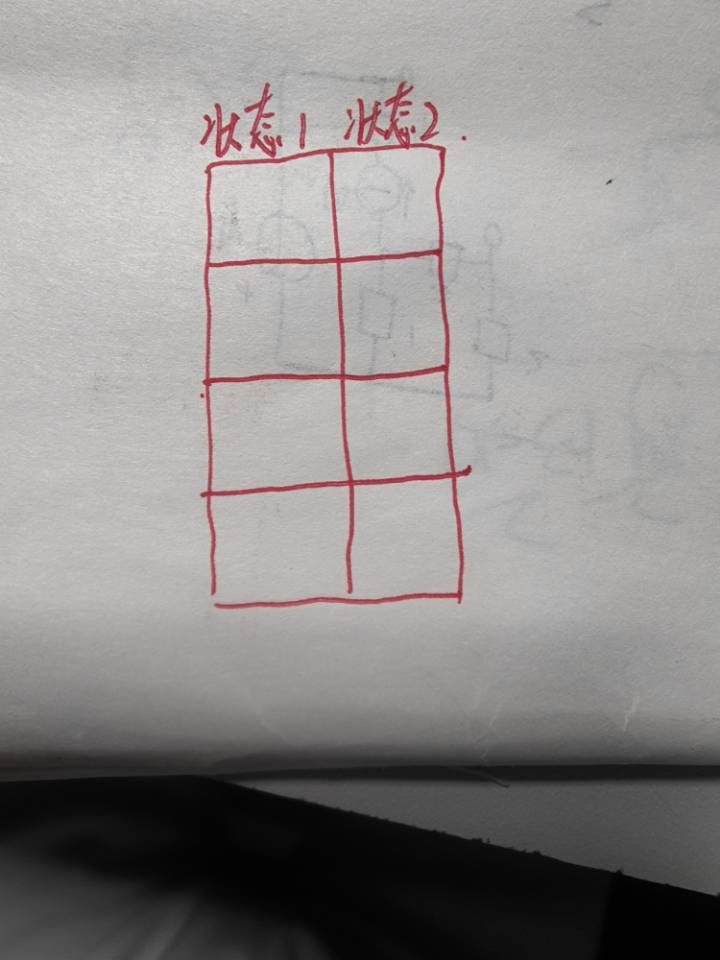
A:
两种状态为奇数天加偶数天减
思路:倒退出该问题的子问题,奇数天的时候,需要加能量,这时候要进行比较,上一个偶数天的最大能量值加该天的能量和上一个奇数天的最大能量值相比较,取最大值,反之,偶数天的时候,需要减能量,让上一个奇数天的最大能量值减该天的能量值与上一个偶数天的最大能量值相比较,取最大值,因为天数从1开始,那么就要定义一个为0的数组用来减一的比较,初始化为0,到最后再让最后一个奇数天的最大值和最后一个偶数天的最大能量值相比较,取最大的输出
代码如下:
#include <iostream>
using namespace std;
int max(int a,int b)
{
if(a>b) return a;
return b;
}
int main()
{
int a[2][150005];//a[0][i]表示偶数天数所获得的最大能量,a[1][i]表示奇数天数所获得的最大能量
int n,p,ma;
while(cin>>n)
{
a[0][0]=0;
a[1][0]=0;
for(int i=1;i<=n;i++)//因为i=0的时候天数为0,所以天数是从i=1时开始的,结束自然也是i=n时
{
cin>>p;
a[0][i]=max(a[0][i-1],a[1][i-1]-p);//输入p后,把上一个偶数天数的值和上一个奇数天数的值-p相比较,取最大值
a[1][i]=max(a[1][i-1],a[0][i-1]+p);//反之,亦然
}
ma=max(a[0][n],a[1][n]);
cout<<ma<<endl;
}
return 0;
}
D:
思路:两种状态为单买和双买,双买时需要与i-2时的两个值相比较,而单买时需要与i-1的两个值比较
这个题如果用printf输出可能更简便
printf("%02d:%02d:%02d %sn",h>12?h-12:h,m,s,h>12?"pm":"am");
控制长度为2,不满2补0
AC代码:
#include <iostream>
#include<algorithm>
using namespace std;
int dp[2][2005];
int a[2005];
int b[2005];
int main()
{
int s,n;
cin>>s;
while(s--)
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=2;i<=n;i++)
cin>>b[i];
dp[0][1]=a[1];
dp[1][1]=a[1];
for(int i=2;i<=n;i++)
{
dp[0][i]=min(dp[0][i-1],dp[1][i-1])+a[i];
dp[1][i]=min(dp[1][i-2],dp[0][i-2])+b[i];
}
int t=min(dp[0][n],dp[1][n]);
int s=t%60;
int m=(t/60)%60;
int h=8+t/3600;
if(h<10) cout<<"0"<<h<<":";
else cout<<h<<":";
if(m<10) cout<<"0"<<m<<":";
else cout<<m<<":";
if(s<10) cout<<"0"<<s<<" ";
else cout<<s<<" ";
if(h<12) cout<<"am"<<endl;
else cout<<"pm"<<endl;
}
return 0;
}
R:
思路:两种状态,一种为大写键开启,一种为小写键开启,大写键开启表示输完该字母后状态为大写,小写键开始表示输完该字母后状态为小写
#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
int dp[2][105];//dp[1][i]表示大写键打开,dp[0][i]表示大写键关闭
int main()
{
int n;
cin>>n;
while(n--)
{
dp[1][0]=1;
string s;
cin>>s;
for(int i=0;i<s.length();i++)
{
if(s[i]<='z'&&s[i]>='a')
{
dp[1][i+1]=min(dp[1][i]+2,dp[0][i]+2);
dp[0][i+1]=min(dp[1][i]+2,dp[0][i]+1);
}
else
{
dp[1][i+1]=min(dp[1][i]+1,dp[0][i]+2);
dp[0][i+1]=min(dp[1][i]+2,dp[0][i]+2);
}
}
cout<<min(dp[1][s.length()]+1,dp[0][s.length()])<<endl;
}
return 0;
}
M:
思路:进行问题简化,因为不知道l的数值,所以应该用两个数组对数值进行存储,并依次求出最大值,比较两个最大值取最大值,输出结果,注意使用long long长整型
AC代码:
#include <iostream>
#include <cmath>
using namespace std;
long long a[100010],b[100010],c[100010];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=1;i<n;i++)
{
if(i%2==1)
{
b[i]=abs(a[i]-a[i+1]);
c[i]=-abs(a[i]-a[i+1]);
}
else
{
b[i]=-abs(a[i]-a[i+1]);
c[i]=abs(a[i]-a[i+1]);
}
}
long long msum=0,tsum=0;
for(int i=1;i<n;i++)
{
tsum+=b[i];
if(tsum>msum)
msum=tsum;
else if(tsum<0)
tsum=0;
}
tsum=0;
for(int i=1;i<n;i++)
{
tsum+=c[i];
if(tsum>msum)
msum=tsum;
else if(tsum<0)
tsum=0;
}
cout<<msum;
return 0;
}
做题时的实时总结:
这个P题和T题可把我坑惨了
一开始做的T
T.
只把上课讲的例题略加修改,大体思路还是偏向动态规划的,虽然整体代码看起来比较繁琐,不过这是依照上课所用的模板动脑子最少的一个办法,嘿嘿嘿
思路:还是先用动态规划求出最大值之后,然后来找为最大值时的起始位置
代码如下:
int a[10005],b,end,maxx[10005];//max[i]表示结尾为第i个数时的最大值,end表示最后一个元素的位置,b表示开始的位置
int i,t;//t表示元素个数
while(cin>>t&&t!=0)
{
int m=0;
for(i=1;i<=t;i++)
cin>>a[i];
maxx[1]=max(a[1],0);
end=0;
for(i=2;i<=t;i++)
maxx[i]=max(maxx[i-1]+a[i],0);
for(i=1;i<=t;i++)
{
if(maxx[i]>m)
{
m=maxx[i];
end=i;
}
if(a[i]==0&&end==0)
end=i;
}
b=a[1];
for(i=1;i<=end;i++)
{
if(a[i]<0&&maxx[i]==0)
b=a[i+1];
}
if(end==0)
cout<<m<<' '<<a[1]<<' '<<a[t]<<endl;
else
cout<<m<<' '<<b<<' '<<a[end]<<endl;
}
代码看起来好繁琐…
P.
一开始,我还想像做T那样投机取巧,运用动态规划
maxx[1]=max(a[1],0);
for(i=2;i<=t;i++)
maxx[i]=max(maxx[i-1]+a[i],0);
for(i=1;i<=t;i++)
if(maxx[i]>m)
m=maxx[i];
求出最大值,可是代码调试了一遍又一遍,仍然没有达到预期的效果,在战斗了一小时后,我放弃了动态规划,用普通的算法解决了问题
思路:先让max最大值初始化为一个很小的数,然后定义一个sum变量,初始化为0,从头开始累计元素和,如果累加的过程中,sum出现小于0的时候,让sum重新等于0,并使临时起始位置p赋值为该位置+1,直到出现sum大于max的时候,让起始位置变为p,终止位置即最后一次sum>max的位置
代码如下:
for(i=1;i<=n;i++)
{
sum+=a[i];
if(sum>max)
{
max=sum;
begin=p;
end=i;
}
if(sum<0)
{
sum=0;
p=i+1;
}
}
Q.
这个Q题太有意思了,就像发现了个新大陆,先给大家卖个关子
这是我第一次提交的代码:
#include<iostream>
#include<string.h>
using namespace std;
int max(int a,int b)
{
if(a>b) return a;
return b;
}
int dp[1005][1005];
int main()
{
ios::sync_with_stdio(false);
char str1[1005],str2[1005];
int i,j,L1,L2;
while(1)
{
cin>>str1>>str2;
L1=strlen(str1);
L2=strlen(str2);
memset(dp,0,sizeof(dp));
for(i=1;i<=L1;i++)
{
for(j=1;j<=L2;j++)
{
if(str1[i-1]==str2[j-1])
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
cout<<dp[L1][L2]<<endl;
}
return 0;
}
显示超时Time Limit Exceeded
这是我在看完题解后改的代码(AC):
#include<iostream>
#include<string.h>
using namespace std;
int max(int a,int b)
{
if(a>b) return a;
return b;
}
int dp[1005][1005];
int main()
{
ios::sync_with_stdio(false);
char str1[1005],str2[1005];
int i,j,L1,L2;
while(cin>>str1>>str2)
{
L1=strlen(str1);
L2=strlen(str2);
memset(dp,0,sizeof(dp));
for(i=1;i<=L1;i++)
{
for(j=1;j<=L2;j++)
{
if(str1[i-1]==str2[j-1])
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
cout<<dp[L1][L2]<<endl;
}
return 0;
}
区别在哪?
就像找不同,区别就那么一点,只是把第一个的
while(1)
{cin>>str1>>str2;
...}
改成了
while(cin>>str1>>str2)
{...}
这就从超时变为AC了…看起来让我有点无语,但是也肯定了,while(cin>>str1>>str2)运行所耗费的的时间少于
while(1)
{ cin>>str1>>str2;
...}
那么我又想到了,使用for循环呢?
于是我又把代码改成了
for(;;)
{cin>>str1>>str2;
...}
超时
得出结论while(cin>>str1>>str2)永远滴神,嘿嘿嘿
其实还有一个地方让我觉得很奇怪
int dp[1005][1005];如果定义成全局变量,可以运行,可如果定义在了main函数内,codeblocks编译器运行不了,倒也不是运行不了,而是运行之后马上就结束了,也不知道是什么问题…电脑上就这一个编译器,也没有办法去验证其他的编译器,到目前还不知道到底是什么问题…如果哪个大佬看到,可以帮忙解答一下吗~~
好了,接下来是正文
题意:给两个字符串,一个字符串中含有另一个字符串相同的字符数,但是这些字符的位置必须是另一个字符串字符位置的升序
思路:
一开始我的思路并不是动态规划,而是定义一个char类型的数组之后,然后sort函数排序,然后unique去重,然后使用双重for循环进行比较,但是仔细一读题后发现题意并没有想象的那样简单,于是我又想起来了一开始吃金币的例题,找到了灵感,感觉这两个题有异曲同工之妙,或者说吃金币的题就是动态规划的基本模型,运用二维数组,第一行表示以1字符串的第一个字母为起点在另一个字符串的中相同的字符数,从第二行开始,如果遇到与第二个字符串相同的字符,使表格左上方的数+1,否则取表格上侧和左侧的最大值,二维数组的最后一个,即表格的最右下角的数值就是所求最大值
概念图如图(以字符串acfd和cazhfa为例):
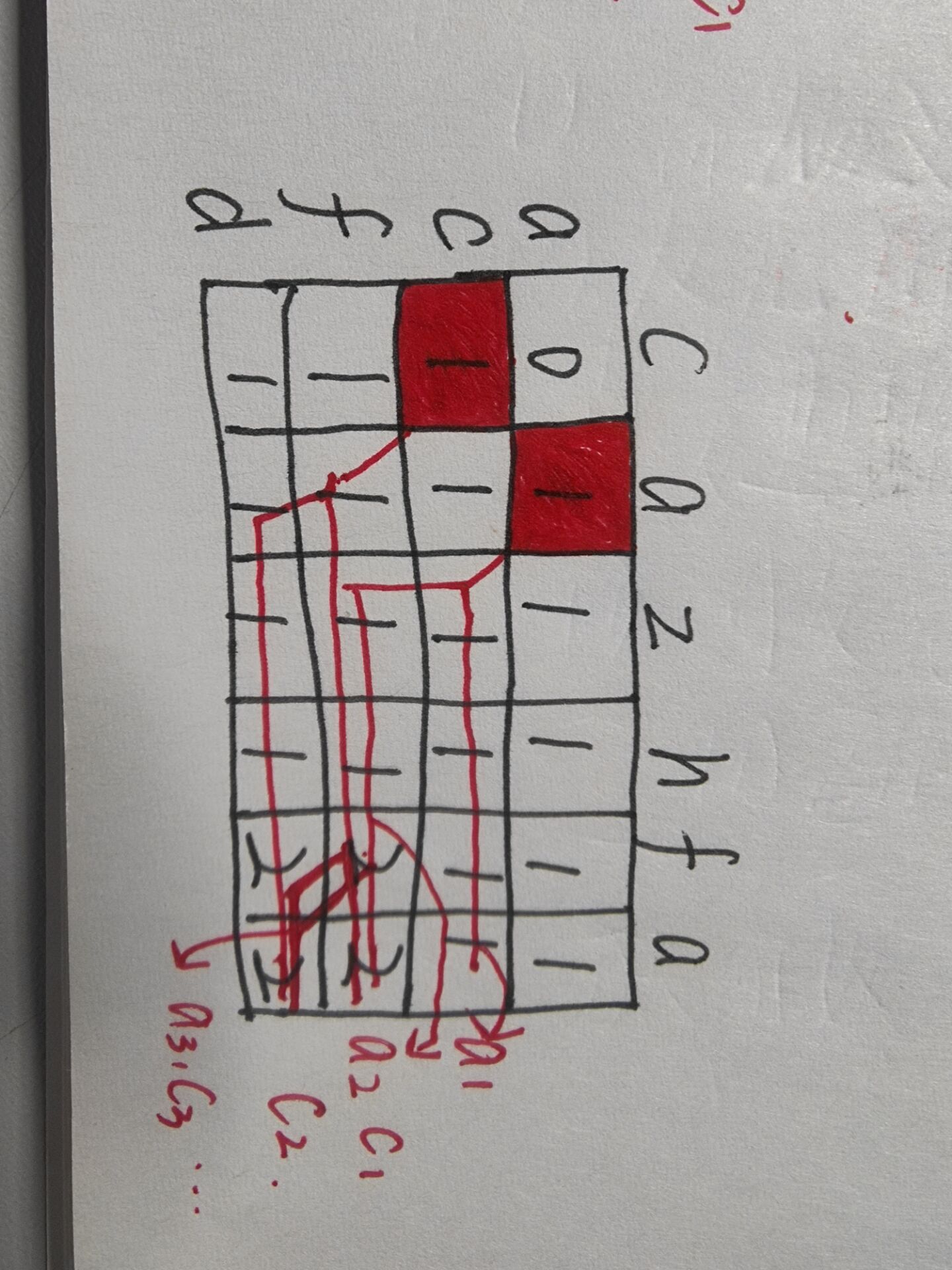
该图的路线的起点有2个,每一个都可以实现题意
以a为起点的线路记为ax
以c为起点的线路记为cx
x表示线路序号
如图,线路a1表示a与a相等后,从右下方开始比较,比较完该行后,没有数值能加,开始a2路线,直到有数值的增加,f和f,继续从右下方开始比较
类似的线路c也是如此,先走c1直到数值增加,走c2路线,继续比较,直到数值增加后走下一条路线
直到走到最右下角为止,结束循环,输出右下角dp的值,即最大值
感想:
最近开始学习动态规划,一开始可以说是毫无思路,听着老师上课讲的内容,讲着讲着就出来了状态转移方程,就感觉好神奇啊,怎么得出来的,慢慢的我觉得动态规划状态转移方程可以用倒推的形式推出来,可是越做越不是那么回事,越来越难找状态转移方程,还是因为作业中的J题Dynamic Programming?给我解释了一下什么是动态规划
Dynamic Programming, short for DP, is the favorite of iSea. It is a method for solving complex problems by breaking them down into simpler sub-problems. It is applicable to problems exhibiting the properties of overlapping sub-problems which are only slightly smaller and optimal substructure.
(动态编程,DP的缩写,是iSea的最爱。 它是通过将复杂问题分解为更简单的子问题来解决的方法。 它适用于表现出重叠子问题的属性的问题,这些子问题仅略微较小且是最佳子结构。)
好像一下点醒了我一样,对啊,动态规划的思想就是将一个复杂的问题分解为一个个子问题分别进行求解,慢慢的可以把一个题目分解成一个个小问题,让困难的问题简化,动态规划难,但如果可以找出其中的规律得出动态转移方程,就不是那么困难了,做题时可以分为三个步骤
1.将每个问题分解成一个个子问题,找出最小的子问题
2.根据子问题找动态关系,得出动态转移方程
3.代码实现
最后
以上就是温柔豆芽最近收集整理的关于动态规划学习总结的全部内容,更多相关动态规划学习总结内容请搜索靠谱客的其他文章。








发表评论 取消回复