在面试中，动态规划是经常考查的题型。如果不能形成系统的思维体系，面试临时思考会造成很大的压力。

今天小编总结动态规划的常用知识点。点赞收藏，面试前看一遍，快速通关动规题型。

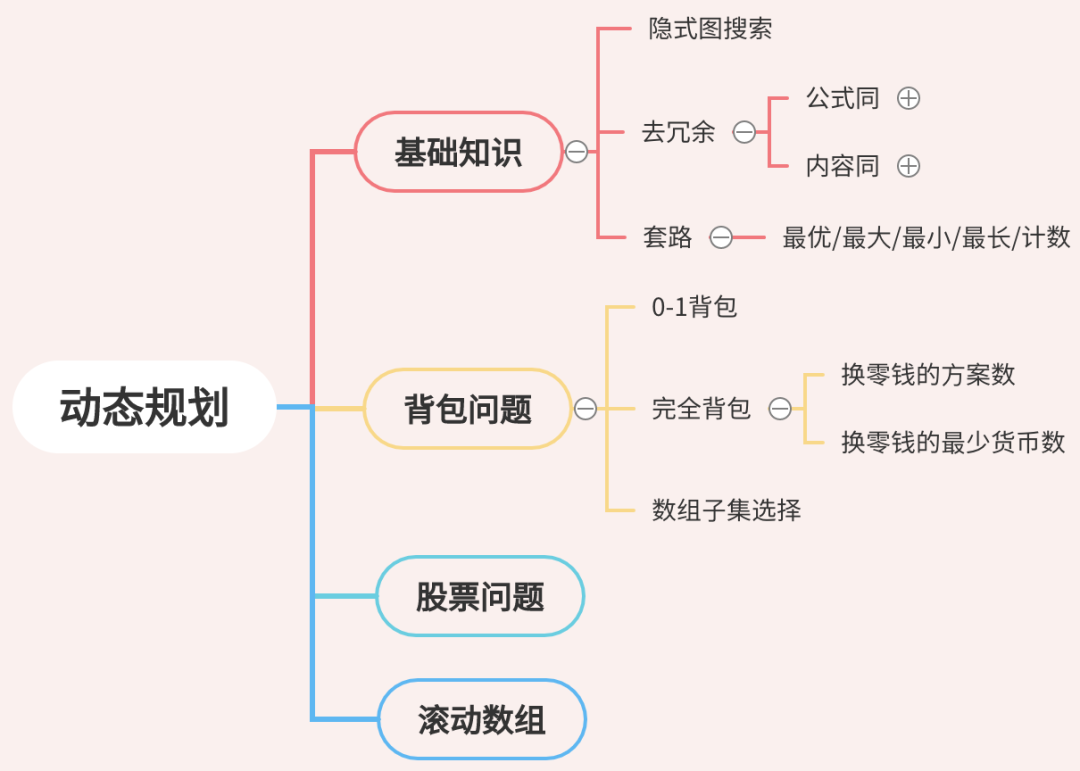
01. 基础知识

1.1 隐式图搜索

动态规划并不是一种解题思路，而是一种去冗余的优化思路。所以在拿到一道题时，第一时间是去考虑怎么常规的解决，而不是直接考虑动态规划。

万金油算法是暴力搜索，暴力搜索实质是枚举了所有的情况，通常可以使用回溯递归来实现。

暴力搜索要明确两件事情：

1. 搜的是什么？

   答：隐式图。先画出来隐式图，暴力搜索就是搜索如下面的隐式图，而发现搜索过程中有冗余搜索行为，才考虑用动态规划来优化。

   

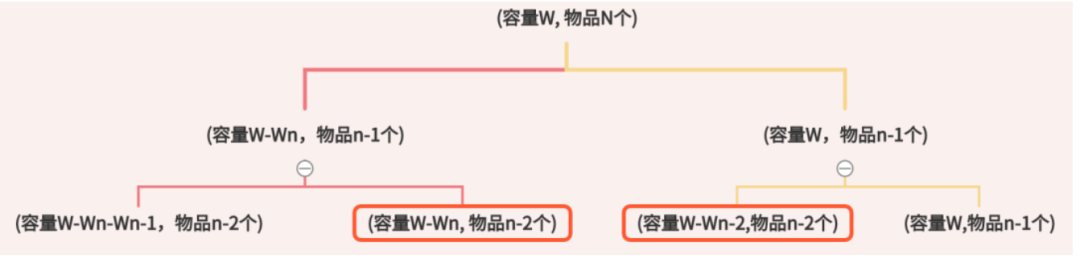
2. 搜到了哪一步？

   答：明确「状态」和「选择」。如上面隐式图中，每个节点都是一个状态，而边代表选择，在每一个状态采用不同选择会导向不同状态。

1.2 去冗余

暴力搜索过程中发现有冗余才会选择动态规划优化。而怎么能发现是否冗余呢？分为公式同和内容同两种。

1. 公式同

隐式图中F(i) = F(i-1)..F(i-2), F(i)不仅与i-1相关还与i-2相关，所以在计算F(i-1)时就有重复部分i-2了

2. 内容同

隐式图中F(a) 与F(b)内容同，即a与b是相同的，就存在冗余计算了。

1.3 套路

1.  看字眼

   出现求最优、最大、最小、最长、计数这种问题时一般可以套用动态规划。

2. 离散问题

   离散问题，只涉及到整数时由于容易设计“状态”，所以可以套用动态规划。

3. 最优子结构

     整个问题可以由于不同的选择，拆解成相同的子问题。此时可以套用动态规划。

02. 背包问题

2.1 完全背包

0-1背包 与 完全背包的区别在于：0-1背包能拿的物品只有一个，完全背包中每个物品可以无限拿。

通过换零钱例题来阐述完全背包问题。

1. 求换零钱方案数

有一个数组所有的值都为正数且不重复。每个值代表一种面值的货币，每种面值的货币可以使用任意张，对于一个给定值x，计算组成这个值的方案数。

此题与硬币的顺序无关，与某种硬币的使用个数有关，因此可以对兑换方式分类。

假设硬币只包含10, 5, 1元这几类。若要兑换50元，则兑换方式可分为：不含10元硬币、含1个10元硬币、含2个10元等情况。这种思路是使用递归来实现暴力搜索。

这道题有重叠子问题，属于内容冗余。例如总共50元，使用10，5，1 来兑换。这样使用“一张10元，0张5元”的；和“0张10元，2张5元”的两个选择都导向了（面值40元，物品还剩1元）的子问题。有重叠子问题，所以采用动态规划来优化解决。

• 首先定义“状态”。

  第一个维度代表可以使用的零钱数组的长度。

  注意：与数组相关的状态，一般定义为数据的长度，而不是数组的下标。因为数组的长度是从1开始的，方便对0进行初始化。

  第二个维度代表剩余的钱金额（即背包容量）。

  dp[i][j]定义为使用前i个元素组成金额j 的方案数。

• 然后定义转移方程。

  从顶向下思考。如隐式图中状态与选择，将整个问题拆分为子问题。

  整个问题定义为使用前i个元素组成金额j 的方案数。有两个选择，分别为不使用第i个元素，和使用第i个元素。

  如果不使用第i个元素，则问题转化为使用前i-1 个元素组成金额j的方案数，即dp[i-1][j]。

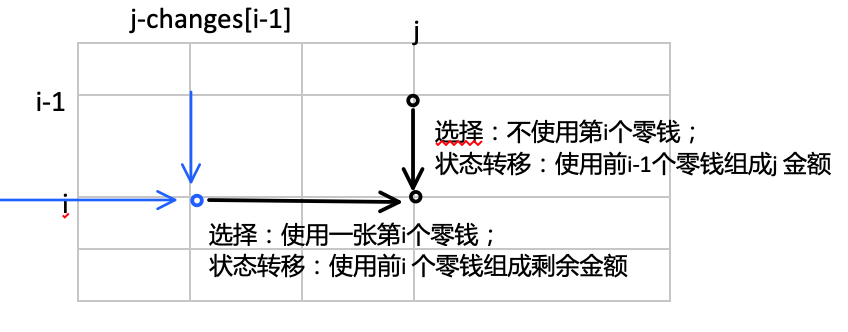
  如果使用第i个元素，由于每个元素可以使用无限次，所以问题转化为使用1个第i个元素，然后仍然用前i 个元素组成剩下金额的方案数，即dp[i][j-changes[i-1]]。(如下图，每一个右箭头，代表使用1次第i个元素，所以向右汇总到dp[i][j]， 就都算上了使用任意次第 i 个元素的情况)

综上，dp[i][j] = dp[i-1][j] +（j-changes[i]>=0?dp[i][j-changes[i-1]]:0)。

• 初始化

  考虑边界条件。仅仅将dp[0][0]置为1。

2. 换钱的最少货币数

仍然是用一组面额来换零钱，但是求能换零成功使用最少的货币数目。

与上题基本相同，改变状态的定义，dp[i][j]定义为使用前i个元素组成金额j 的最小货币数。

• 转移方程

dp[i][j] = min(dp[i-1][j],  dp[i][j-arr[i]]+1  if(j<arr[i]) )。

当其中一个子问题不成立即不能恰好找零，则取另一个子问题的值。

• 初始化

注意初始化与上题不同。

区别在于，当前i个元素不能组成金额j时，其方法个数可以为0，但最小货币数不能为0，应该用 -1 代表不能组成。

所以将dp数组全初始化为-1， 但将dp[all][0]都置为0。

2.2 数组子集选择问题

将问题转化为 「子集划分/选择」 问题，然后再次转化为「 背包问题」。使用动态规划来解决「子集划分/选择」 问题。

详情见往期刷题有术--数组题型技巧汇总

03. 股票问题

先说结论，股票问题给我们的启发，如果实在想不出来转移方程，要将状态升维。

股票买卖问题是求能获取的最大利益。但是题目中可能会有最大交易次数限制，冷冻期限制。

当有了冷冻期或者最大交易次数之后，我们很难想出递推方程。

一个技巧是将条件转变为状态，将dp数组升维，从而简化递推方程式。

股票问题的状态设计为dp[i][k][t], 含义为：

i: 遍历到第i项，k: 交易了k次，t: 当前是有股票还是没有股票，0代表没有股票，1代表有股票。

如下题，在卖出股票过后，第二天是冷冻期，无法买入。

给定一个整数数组prices，其中第  prices[i] 表示第 i 天的股票价格 。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）: 卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。 

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

这时我们设计状态为dp[i][t] 代表遍历到第i项时有股票或者没有股票的最大利润。

所以递推方程式可以写出来：

dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i-1]);

dp[i][1]=max(dp[i-1][1], dp[i-2][0]-prices[i-1])。

04 滚动数组

递推公式满足第一个维度只与前一个i-1有关时，可以通过滚动数组减少存储空间。即舍弃第一个维度，将二维dp数组变为为一维。

用0-1背包问题举个例子，二维数组的递归公式如下：
dp[i][j] = max(dp[i-1][j - w[i]] + value[i], dp[i-1][j])

第一个维度只与前一个i-1有关，优化为一维数组，递推公式如下：

dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

但是注意一维数组遍历时 j 从大到小，因为j 需要依赖上一轮(i-1)的小于j 的元素，所以j需要从大到小遍历，保证小于j的 是上一轮(i-1)的结果。

如下图，代码还是双层for循环，只不过dp[j] 从大到小遍历，保证了前面部分保存的还是上一轮i-1 的结果，随着j 的遍历，逐步将dp[j] 覆盖成这一轮i 的结果。

5. 分享

分享一本好书《程序员代码面试指南：IT名企算法与数据结构题目最优解》。全书一共九章，涉及到了所有常考题目的讲解，非常实用！

评论获取下载链接

最后

以上就是曾经白猫为你收集整理的动态规划，你思考过这些问题吗01. 基础知识02. 背包问题03. 股票问题04 滚动数组的全部内容，希望文章能够帮你解决动态规划，你思考过这些问题吗01. 基础知识02. 背包问题03. 股票问题04 滚动数组所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。