题256.洛谷P1495 中国剩余定理-【模板】中国剩余定理(CRT)/曹冲养猪

一、关于中国剩余定理CRT

1.概述

用于求解如下形式的一元线性同余方程组(b1,b2,…,bk两两互质)：

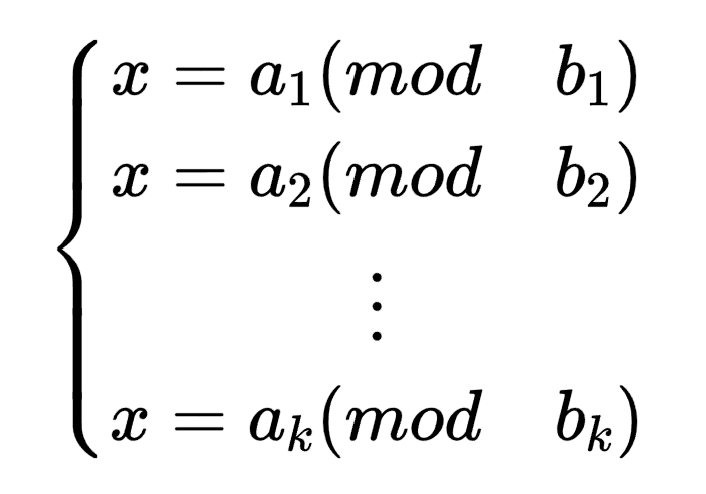
通俗讲就是可以求一个数x，该数对bi求余等于ai，i从1到k。

2.算法步骤
设除数为ai,余数为bi，i∈[0,N)且i∈Z。要求的数为res
①求出所有除数ai的乘积n
②求出ai以外作为所有的除数的倍数m，m=n/ai
③利用扩展欧几里得算法或者费马小定理得到m的逆元mm

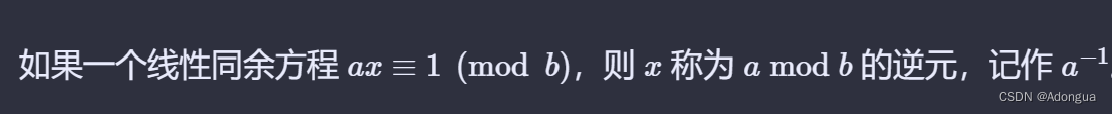
此为m*mm≡1(mod ai)，即解线性同余方程m*mm+ai*y=1，有代码：

//扩展欧几里得算法求逆元（要求gcd(a,b)=1，即a，b互质）
void ex_gcd(int a, int b, int& x, int& y) {
  if (b == 0) {
    x = 1, y = 0;
    return;
  }
  ex_gcd(b, a % b, y, x);
  y -= a / b * x;
}

//快速幂+费马小定理（要求b为质数）
ll fastpow(ll base,ll pow)//a,b
{
    ll res=1;
    while(pow)
    {
        if(pow&1) res=res*base%b;
        pow>>=1;
        base=base*base%b;
    }
    return res;
}
ll res=fastpow(a,b-2)%b;//a^(-1)=a^(b-2)

④将m乘以mm乘以余数bi，把结果加到res中。若总结果看起来可能会很大，就按取模公式做取模运算
⑤i++，回到②，当i=N时结束操作

二、题目

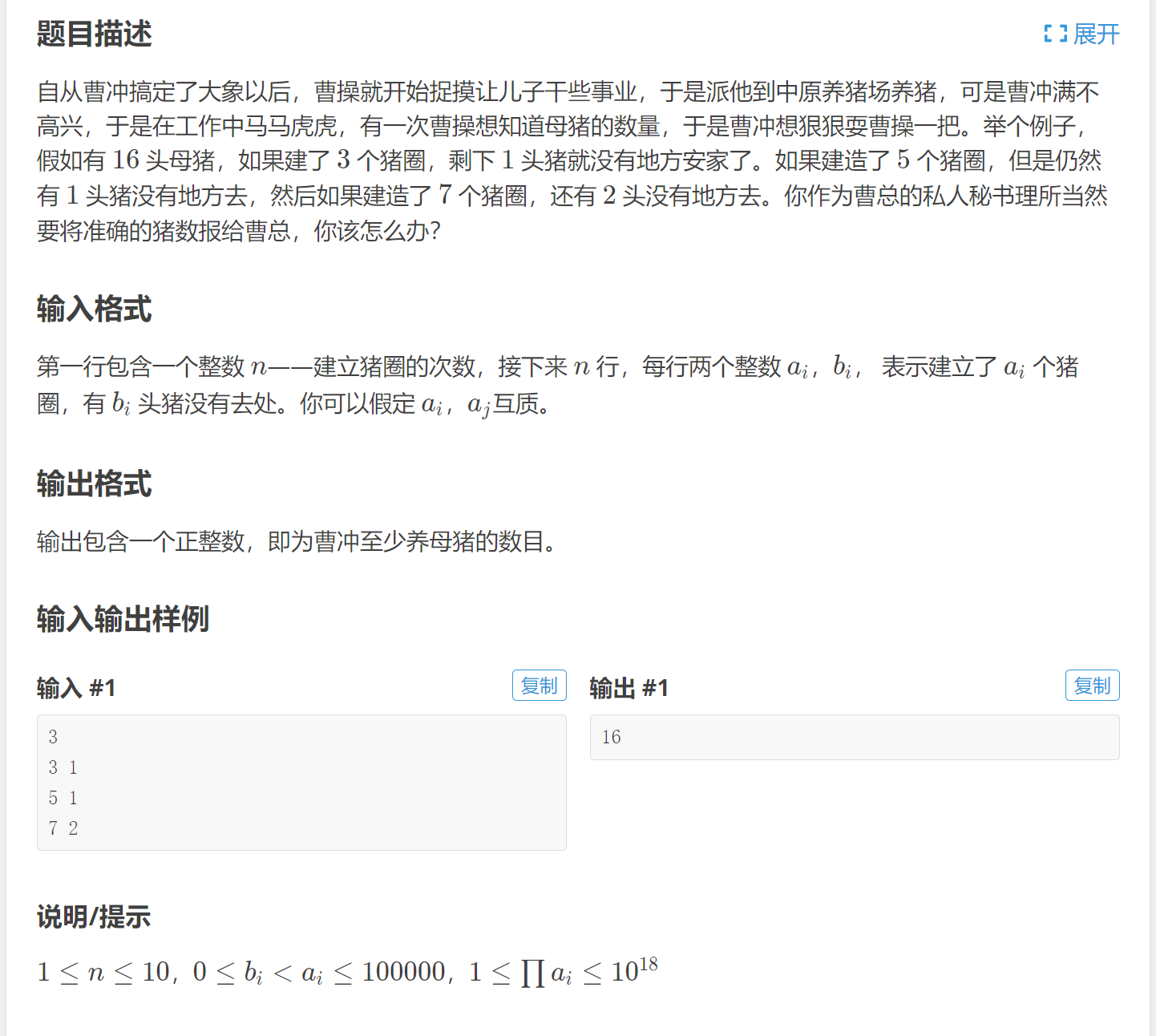
三、题解

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn=1e5+1;

ll a[maxn],b[maxn];

ll ex_gcd(ll a,ll b,ll &x,ll &y)//扩展欧几里得算法
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    ll ans=ex_gcd(b,a%b,x,y);
    ll tmp=x;
    x=y;
    y=tmp-a/b*y;
    return ans;
}

ll CRT(ll a[],ll b[],int N)
{
    ll n=1;
    for(int i=0;i<N;i++)//得到所有除数的乘积
    {
        n*=a[i];
    }
    ll res=0;
    for(int i=0;i<N;i++)
    {
        ll m=n/a[i];//得到a[i]以外所有的除数的倍数m
        ll mm,y;
        //利用扩欧求m的逆元mm
        ex_gcd(m,a[i],mm,y);
        mm=(mm%a[i]+a[i])%a[i];//最小正整数x为(x%b/gcd(a,b)+b/gcd(a,b))%b/gcd(a,b)
        res=(res%n+m*mm*b[i]%n)%n;//线性同余方程组的唯一解res为(m*mm*余数)求和
    }
    return res;
}

int main()
{
    int N;
    cin>>N;
    for(int i=0;i<N;i++)
    {
        cin>>a[i]>>b[i];
    }
    ll res=CRT(a,b,N);
    cout<<res;
}

//二刷代码
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int maxn=11;

int N;
ll a[maxn],b[maxn];

ll ex_gcd(ll a,ll b,ll &x,ll &y)
{
    if(!b)
    {
        x=1,y=0;
        return a;
    }
    else
    {
        ll d=ex_gcd(b,a%b,y,x);
        y-=a/b*x;
        return d;
    }
}

int main()
{
    cin>>N;
    ll n=1;
    for(int i=0;i<N;i++)
    {
        cin>>a[i]>>b[i];
        n*=a[i];
    }
    ll res=0;
    for(int i=0;i<N;i++)
    {
        ll m=n/a[i];
        ll mm,y;
        ex_gcd(m,a[i],mm,y);
        res+=b[i]*m*mm;
    }
    cout<<(res%n+n)%n;
}

关于CRT的详解可以进一步看看牛人的这篇文章以及oi-wiki

最后

以上就是强健酸奶为你收集整理的题256.洛谷P1495 中国剩余定理-【模板】中国剩余定理(CRT)/曹冲养猪题256.洛谷P1495 中国剩余定理-【模板】中国剩余定理(CRT)/曹冲养猪一、关于中国剩余定理CRT二、题目三、题解的全部内容，希望文章能够帮你解决题256.洛谷P1495 中国剩余定理-【模板】中国剩余定理(CRT)/曹冲养猪题256.洛谷P1495 中国剩余定理-【模板】中国剩余定理(CRT)/曹冲养猪一、关于中国剩余定理CRT二、题目三、题解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。