matlab二叉树期权计算delta值,期权delta值计算公式,深度实值期权杠杆

66 阅读 0 评论 44 点赞

我是靠谱客的博主危机长颈鹿，最近开发中收集的这篇文章主要介绍matlab二叉树期权计算delta值,期权delta值计算公式,深度实值期权杠杆，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

你知道Black-Scholes的公式吗？里面的N(d1)就是看涨期权的Delta，看跌的就是1－N(d1)。如果知道这个公式的话就可以不用看下面的内容了。下面只是维基百科搬运来的公式而已。

就是下面这个公式：(我只拿了看涨的举例，想看看跌的去这个链接，维基百科：http://en.wikipedia.org/wiki/Black%E2%80%93Scholes_model#Black-Scholes_formula)

其中：

T是到期时间(单位年)

K是执行价格

e是欧拉数

r是无风险利率

小写的Sigma是波动率(现实中这个数是用市场价格倒推出来的隐含波动率)

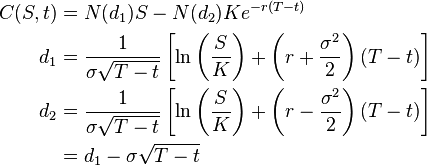
式子第一行左边的C(S,t)表示看涨期权的价格，两个变量S是标的物价格，t是已经经过的时间(单位年)，其他都是常量。Delta的定义就是期权价格对标的物价格的一阶导数，所以右手边对S求一阶偏导，就只剩下N(d1)了。d1的公式也在上面了，把数字带进去就好了。N是标准正态分布的累积分布(需要计算器或者查表)。

最方便的方法，去这个网址：http://www.soarcorp.com/black_scholes_calculator.jsp 可以计算价格和各种Greeks。

已知价格想倒退隐含波动率去这里：http://www.soarcorp.com/black_scholes_implied_volatility_calculator.jsp