数据科普：定价模型与平价关系式（投资必知必会）

hi，凹凸们????

今天给大家介绍一下定价模型与平价关系式。前文链接：期权类型与到期盈亏（投资必知必会）

一、布莱克-斯科尔斯-默顿模型

在20世纪70年代初，费希尔·布莱克( Fisher black)、迈伦·斯科尔斯( Myron Scholes)和罗伯特·默顿( Robert Merton)在对欧式股票期权定价研究方面取得了重大的理论突破，提出了针对欧式期权定价的模型，该模型被称为布莱克-斯科尔斯-默顿模型(简称BSM模型)。

模型假设：

在推导出布莱克斯科尔斯-默顿模型时，有以下7个假设前提条件：

一是假设基础资产的股票价格服从几何布朗过程；二是可以卖空证券，并且可以完全运用卖空所获得的资金；三是无交易费用和无税收，所有证券均可无限分割；四是在期权期限内，基础资产无期间收入(比如股票不支付股息)；五是市场不存在无风险套利机会；六是证券交易是连续进行的；七是短期无风险利率是一个常数，并对所有期限都是相同的。

微分方程：

此外，模型在推导过程中运用到了一个很重要的微分方程，具体就是

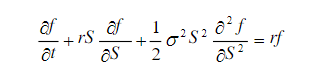
其中，式子中的 f 表示看涨期权价格，S表示期权基础资产的价格，r为连续复利的无风险收益率，σ为基础资产价格百分比变化(收益率)的波动率，t是时间变量。

定价公式：

欧式看涨期权的定价公式

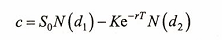
通过看涨-看跌平价关系式，可以得到看跌期权的定价公式：

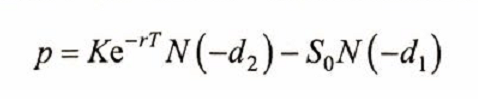
其中：

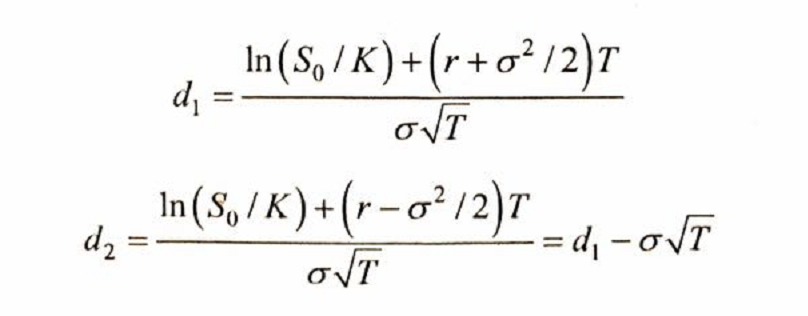
c与p分别代表欧式看涨、看跌期权的价格，S0是基础资产在初始0时刻的价格，K是期权的执行价格，r是连续复利的无风险收益率，σ为基础资产价格百分比变化(收益率)的年化波动率，T是期权合约的期限(单位是年)，N()表示累积标准正态分布的概率密度。

代码实现基于布莱克-斯科尔斯-默顿模型计算欧式看涨期权、看跌期权定价的函数：

import numpy as np
from scipy.stats import norm

def call_BS(S,K,sigma,r,T):
    '''用bs模型计算欧式看涨期权价格
    S 期权基础资产价格
    K 期权执行价格
    sigma 基础资产价格百分比变化（收益率）的年化波动率
    r 无风险收益率
    T 期权合约剩余年限
    '''
    d1 = (np.log(S/K) + (r + pow(sigma,2)/2)*T) / (sigma*np.sqrt(T))
    d2 = d1 - sigma*np.sqrt(T)
    return S*norm.cdf(d1) - K*np.exp(-r*T)*norm.cdf(d2)

def put_BS(S,K,sigma,r,T):
    '''用bs模型计算欧式看跌期权价格
    S 期权基础资产价格
    K 期权执行价格
    sigma 基础资产价格百分比变化（收益率）的年化波动率
    r 无风险收益率
    T 期权合约剩余年限
    '''
    d1 = (np.log(S/K) + (r + pow(sigma,2)/2)*T) / (sigma*np.sqrt(T))
    d2 = d1 - sigma*np.sqrt(T)
    return K*np.exp(-r*T)*norm.cdf(-d2) - S*norm.cdf(-d1)

例子：

一份期限为6个月的股票期权，期权的基础资产是工商银行的A股股票,2018年12月28日股票收盘价是5.29元/股，期权的执行价格为6元股，无风险利率为年化4%，股票收益率的年化波动率是24%，运用布莱克斯科尔斯-默顿模型计算看涨期权看跌期权的价格。

call_BS(S=5.29, K=6, sigma=0.24, r=0.04, T=0.5)
put_BS(S=5.29, K=6, sigma=0.24, r=0.04, T=0.5)

二、看涨-看跌期权 平价关系式

具有相同执行价格与期限的欧式看跌期权、看涨期权在价格上有一个重要关系式。

1.两个投资组合

首先，考虑以下两个投资组合在期权合约到期时的盈亏情况。A投资组合：一份欧式看涨期权和一份在T时刻到期的本金为K的零息债券；B投资组合：一份欧式看跌期权和一份基础资产。这里需要假设看涨期权与看跌期权具有相同的执行价格K与相同的合约期限T。

对于A投资组合而言，零息债券在期权合约到期日(T时刻)的价值显然是等于K，而对于看涨期权则分两种情形讨论。

情形1：如果在T时刻，基础资产价格St>K，A投资组合中的欧式看涨期权将被执行，此时，A投资组合的价值是(St-K)+K=St；

情形2：如果在T时刻，基础资产价格St<K，A投资组合中的欧式看涨期权就没有价值，此时A投资组合的价值为K。

对于B投资组合而言，也分两种情形讨论。

情形1：如果在T时刻，基础资产价格St>K，此时，B投资组合中的欧式看跌期权没有价值，此时，B投资组合价值为St，也就是仅剩下基础资产的价值；

情形2：如果在T时刻，基础资产价格St<K，此时，B投资组合中的欧式看跌期权会被行使，此时B投资组合价值为(K-St)+St=K。综合以上的分析，当St>K时，在T时刻两个投资组合的价值均为St；当St<K时在T时刻两个投资组合的价值均为K。换而言之，在T时刻(期权合约到期时)，两个投资组合的价值均为max(St, K)

由于A投资组合与B投资组合中的期权均为欧式期权，在期权到期之前均不能行使，既然两个投资组合在T时刻均有相同的收益，在期权合约的存续期内也应该有相同的价值。否则，就会出现无风险套利机会，套利者可以买入价格低的投资组合，与此同时卖空价格高的投资组合进行无风险的套利，无风险套利收益就是等于两个组合价值的差额。

2. 抽象的数学表达式

看涨期权 + 零息债券价格 = 看跌期权 + 基础资产价格

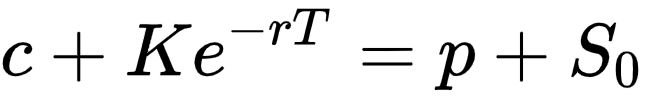
代码实现：

def call_parity(p,S,K,r,T):
    '''通过平价关系式用看跌期权价格计算欧式看涨期权价格。
    p：欧式看跌期权价格
    S：期权基础资产价格
    K：执行价格
    r：无风险收益率
    T：合约剩余期限    
    '''
    return p + S - K * np.exp(-r * T)

def put_parity(c,S,K,r,T):
    '''通过平价关系式，用看涨期权价格计算欧式看跌期权价格。
    c：欧式看涨期权价格
    S：期权基础资产价格
    K：执行价格
    r：无风险收益率
    T：合约剩余期限    
    '''
    return c + K * np.exp(-r * T) - S

例子：

假设当前股票价格为20元股，期权的执行价格为18元/股，无风险收益率为每年5%,3个月的欧式看涨期权价格对外报价是2.3元,3个月的欧式看跌期权对外报价是0.3元，期权价格是否合理？

call_parity(p=0.3, S=20, K=18, r=0.05, T=0.25)
==>2.523599591110134
put_parity(c=2.3, S=20, K=18, r=0.05, T=0.25)
==>0.07640040888986732

通过计算，看涨期权被低估，看跌期权则被高估，因此可以通过持有看涨期权的多头头寸并买入零息债券(相当于买入A投资组合)，同时持有看跌期权的空头头寸并卖空基础资产（相当于卖空B投资组合），从而实现无风险套利。