引入

  一般来说，对于输入为$n_h\times n_w$的矩阵，以及$k_h\times k_w$的核矩阵，互相关运算后，输出的形状将会是：
$$(n_h-k_h+1)\times (n_w-k_w+1).\text{\hspace{1em}(1)}$$  因此，卷积层的输出形状是由输入形状和卷积核矩阵形状决定。
  本节主要介绍卷积层的两个超参数，即填充和步幅：可以对给定形状的输入和卷积核改变输出形状。

1 填充

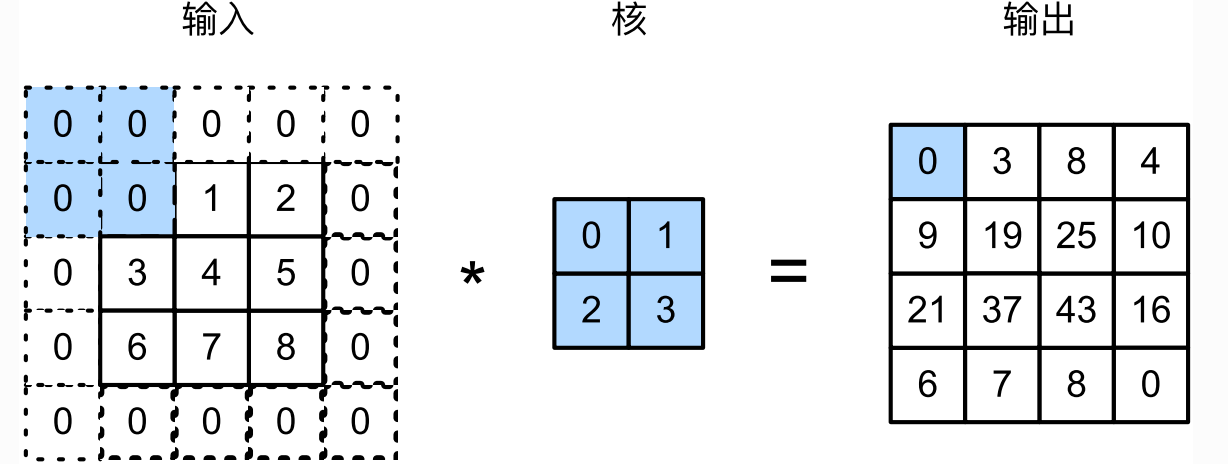
  填充 (padding)是指在输入高和宽的两侧填充元素 (通常为$0$)。例如下图中 (图片源自原书)，对输入矩阵的两侧分别添加了$0$值，使得输入由$3\times 3$变为$5\times 5$，从而导致输出由$2\times 2$变为$4\times 4$。

  一般来说，如果在高的两侧一共填充$p_h$行，在宽的两侧一共填充$p_w$列，那么输出形状将会是：
$$(n_h-k_h+p_h+1)\times (n_w-k_w+p_w+1).\text{\hspace{1em}(2)}$$  很多情况下，会设置$p_h=k_h-1$、$p_w=k_w-1$来使得输入输出具有相同的形状。这样做的好处为，在构造网络时可以推测每个层的输出形状。
  具体的，假设$k_h$是奇数，会在输入上下分别填充$p_h/2$行；偶数，则在输入的顶端填充$\lceil p_h/2\rceil$，在输入的下端填充$\lfloor p_h/2\rfloor$行。$k_w$同理。
  在卷积神经网络中，经常使用奇数高宽的卷积核，如$1$、$3$、$5$和$7$等，所有在两端的填充个数相等。
  对于任意的二维数组$x=[x_{ij}]$，荡两端的填充个数相等，且使输入和输出具有相同的高和宽时，就能知道输出$y=[y_{ij}]$是由输入以$x$为中心的窗口同卷积核进行互相关计算得到的。

import torch
import warnings
import torch.nn as nn
warnings.filterwarnings('ignore')


def comp_conv2d(conv2d, x):
    # 1, 1: Single batch and single channel.
    x = x.view((1, 1) + x.shape)
    y = conv2d(x)
    return y.view(y.shape[2:]) # Do not consider the batch and channel.


if __name__ == '__main__':
    torch.manual_seed(1)
    temp_conv2d = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, padding=1)
    temp_x = torch.rand(2, 2)
    print(temp_x)
    print(comp_conv2d(temp_conv2d, temp_x))

  输出如下：

tensor([[0.6387, 0.5247],
        [0.6826, 0.3051]])
tensor([[-0.0065, -0.1006],
        [-0.3219,  0.0027]], grad_fn=<ViewBackward>)

  该设置下，输入与输出将是等大小。
  当然，当核矩阵的高与宽不同时，也可设置不同的填充数：

if __name__ == '__main__':
    torch.manual_seed(1)
    temp_conv2d = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=(3, 5), padding=(1, 2))
    temp_x = torch.rand(2, 2)
    print(temp_x)
    print(comp_conv2d(temp_conv2d, temp_x))

  输出如下：

tensor([[0.5725, 0.4980],
        [0.9371, 0.6556]])
tensor([[ 0.0922,  0.0855],
        [ 0.1551, -0.0771]], grad_fn=<ViewBackward>)

2 步幅

  步幅 (stride)用于控制每次窗口滑动的行数和列数。一个例子如下图。

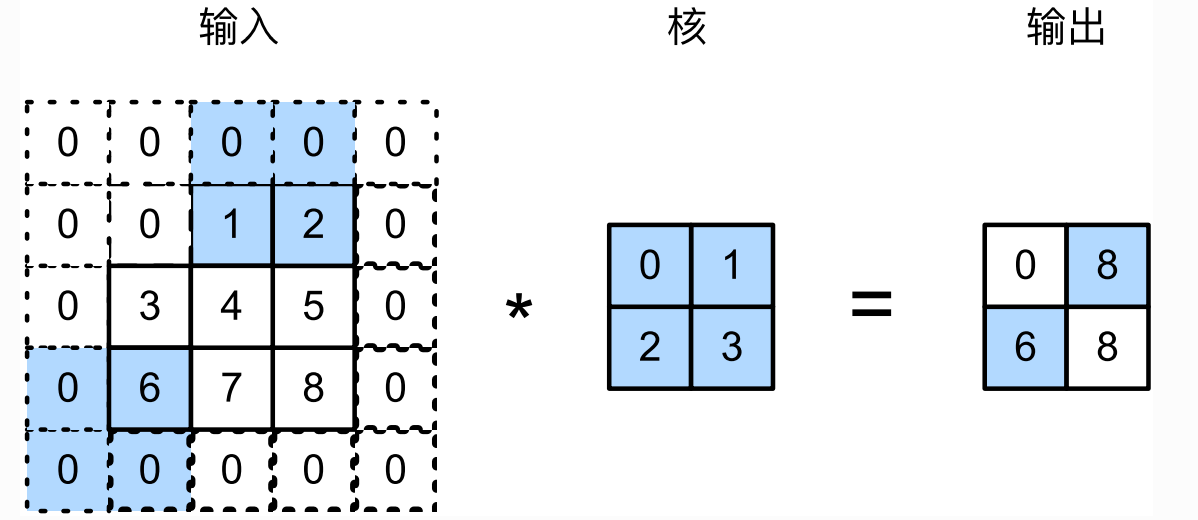
  一般来说，当高上步幅为$s_h$，宽上步幅为$s_w$时，输出的形状为
$$\lfloor (n_h-k_h+p_h+s_h)/s_h\rfloor \times \lfloor (n_w-k_w+p_w+s_w)/s_w\rfloor .\text{\hspace{1em}(3)}$$  进一步，如果设置$p_h=k_h-1$和$p_W=k_w-1$，那么输出的形状将为
$$\lfloor (n_h+s_h-1)/s_h\rfloor \times \lfloor (n_w+s_w-1)/s_w\rfloor .\text{\hspace{1em}(4)}$$  更进一步，如果输入的高和宽能分别被高和宽上的步幅整除，则输出形状为 $(n_h/s_h)\times (n_w/s_w)$。
  torch中，只需设置stride参数：

if __name__ == '__main__':
    torch.manual_seed(1)
    temp_conv2d = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=(3, 5), padding=(1, 2), stride=2)
    temp_x = torch.rand(2, 2)
    print(temp_x)
    print(comp_conv2d(temp_conv2d, temp_x))

  输出如下：

tensor([[0.5725, 0.4980],
        [0.9371, 0.6556]])
tensor([[0.0922]], grad_fn=<ViewBackward>)

参考文献
[1] 李沐、Aston Zhang等老师的这本《动手学深度学习》一书。

最后

以上就是虚拟缘分为你收集整理的torch学习 (十七)：填充和步幅引入1 填充2 步幅的全部内容，希望文章能够帮你解决torch学习 (十七)：填充和步幅引入1 填充2 步幅所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。