背包问题
假设你是个小偷,背着一个可装4磅东西的背包。你可盗窃的商品有如下3件。
为了让盗窃的商品价值最高,你该选择哪些商品?

简单算法
最简单的算法如下:尝试各种可能的商品组合,并找出价值最高的组合。
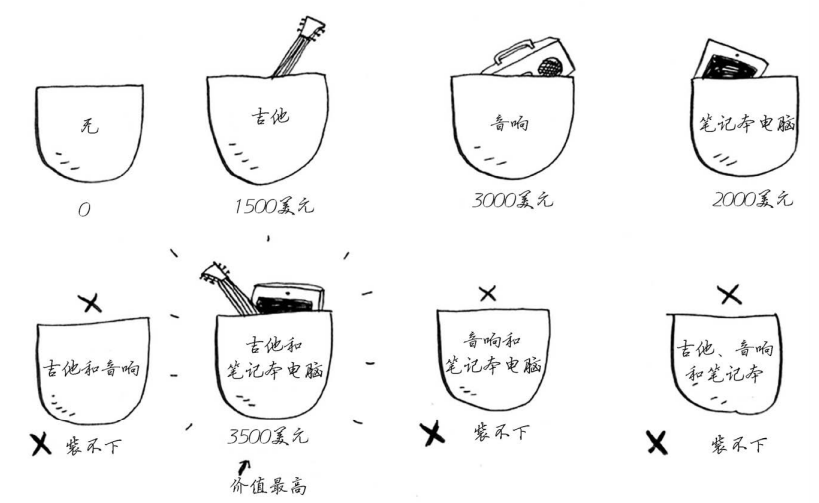
这样可行,但速度非常慢。在有3件商品的情况下,你需要计算8个不同的集合;有4件商品时,你需要计算16个集合。每增加一件商品,需要计算的集合数都将翻倍!这种算法的运行时间为O(2n),真的是慢如蜗牛。只要商品数量多到一定程度,这种算法就行不通。
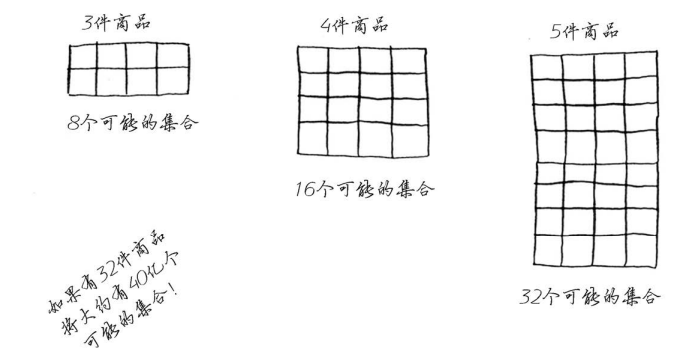
动态规划
答案是使用动态规划!下面来看看动态规划算法的工作原理。动态规划先解决子问题,再逐步解决大问题。
对于背包问题,你先解决小背包(子背包)问题,再逐步解决原来的问题。
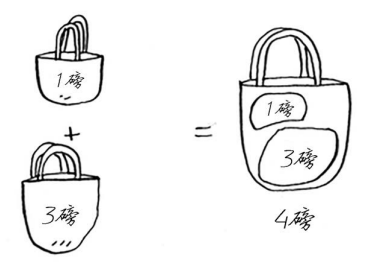
动态规划是一个难以理解的概念,如果你没有立即搞懂,也不用担心,我们将研究很多示例。先来演示这种算法的执行过程。看过执行过程后,你心里将有一大堆问题!我将竭尽所能解答这些问题。
每个动态规划算法都从一个网格开始,背包问题的网格如下。
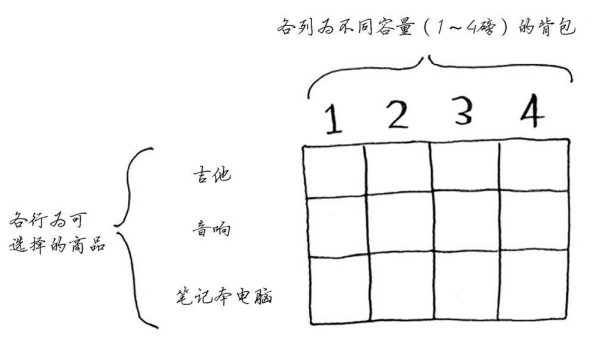
网格的各行为商品,各列为不同容量(1~4磅)的背包。所有这些列你都需要,因为它们将帮助你计算子背包的价值。
网格最初是空的。你将填充其中的每个单元格,网格填满后,就找到了问题的答案!你一定要跟着做。请你创建网格,我们一起来填满它。
1. 吉他(第一行)
后面将列出计算这个网格中单元格值的公式。我们先来一步一步做。首先来看第一行。
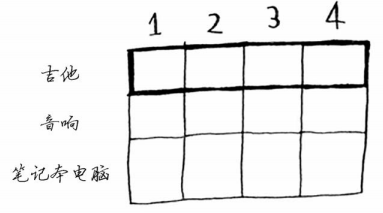
这是吉他行,意味着你将尝试将吉他装入背包。在每个单元格,都需要做一个简单的决定:
偷不偷吉他?别忘了,你要找出一个价值最高的商品集合。
第一个单元格表示背包的容量为1磅。吉他的重量也是1磅,这意味着它能装入背包!因此这个单元格包含吉他,价值为1500美元。
下面来开始填充网格。
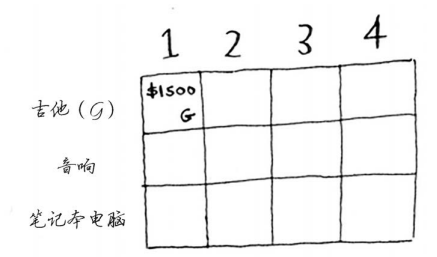
与这个单元格一样,每个单元格都将包含当前可装入背包的所有商品。
来看下一个单元格。这个单元格表示背包的容量为2磅,完全能够装下吉他!
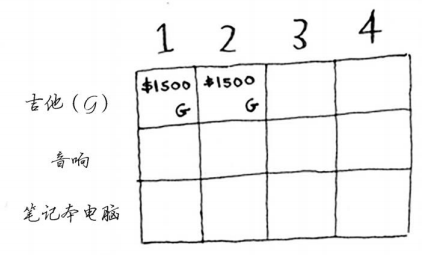
这行的其他单元格也一样。别忘了,这是第一行,只有吉他可供你选择。换言之,你假装现在还没法盗窃其他两件商品。
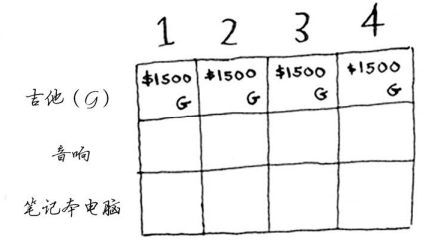
此时你很可能心存疑惑:原来的问题说的是4磅的背包,我们为何要考虑容量为1磅、 2磅等的背包呢?前面说过,动态规划从小问题着手,逐步解决大问题。这里解决的子问题将帮助你解决大问题。请接着往下读,稍后你就会明白的。
此时网格应类似于下面这样。
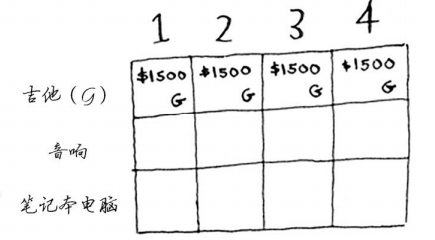
别忘了, 你要做的是让背包中商品的价值最大。 这行表示的是当前的最大价值。它指出,如果你有一个容量4磅的背包,可在其中装入的商品的最大价值为1500美元。
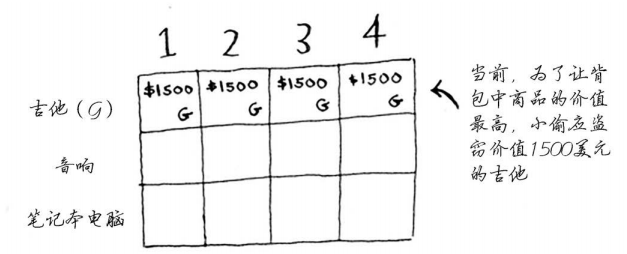
你知道这不是最终的解。随着算法往下执行,你将逐步修改最大价值。
2. 音响行
我们来填充下一行——音响行。你现在出于第二行,可偷的商品有吉他和音响。在每一行,可偷的商品都为当前行的商品以及之前各行的商品。因此,当前你还不能偷笔记本电脑,而只能偷音响和吉他。我们先来看第一个单元格,它表示容量为1磅的背包。在此之前,可装入1磅背包的商品的最大价值为1500美元。
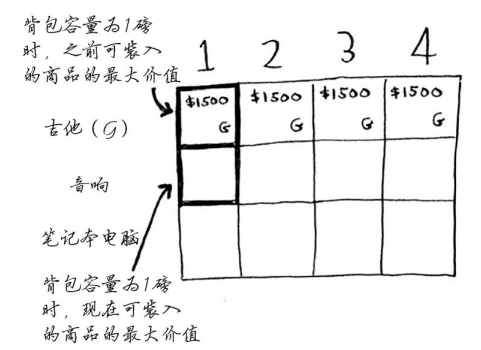
该不该偷音响呢?
背包的容量为1磅,能装下音响吗?音响太重了,装不下!由于容量1磅的背包装不下音响,
因此最大价值依然是1500美元。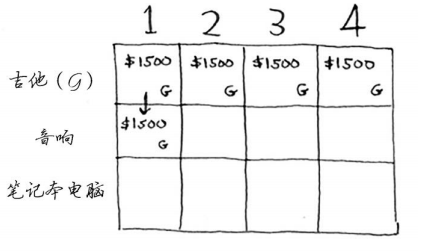
接下来的两个单元格的情况与此相同。在这些单元格中,背包的容量分别为2磅和3磅,而以前的最大价值为1500美元。
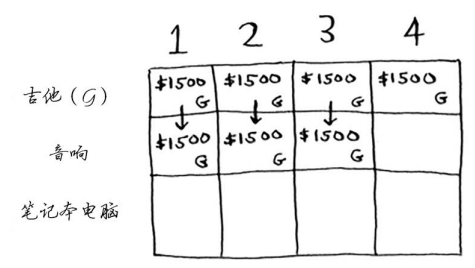
由于这些背包装不下音响,因此最大价值保持不变。
背包容量为4磅呢?终于能够装下音响了!原来的最大价值为1500美元,但如果在背包中装入音响而不是吉他,价值将为3000美元!因此还是偷音响吧。
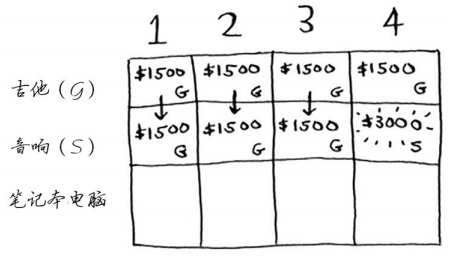
你更新了最大价值!如果背包的容量为4磅,就能装入价值至少3000美元的商品。在这个网格中,你逐步地更新最大价值。
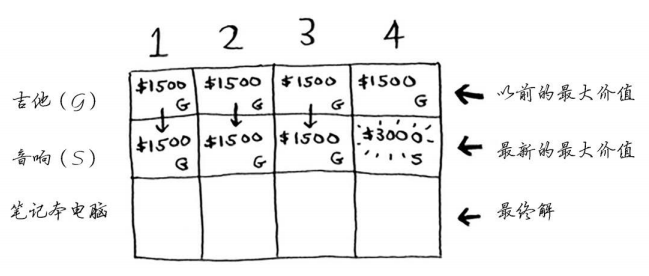
3. 笔记本电脑行
下面以同样的方式处理笔记本电脑。笔记本电脑重3磅,没法将其装入容量为1磅或2磅的背包,因此前两个单元格的最大价值还是1500美元。
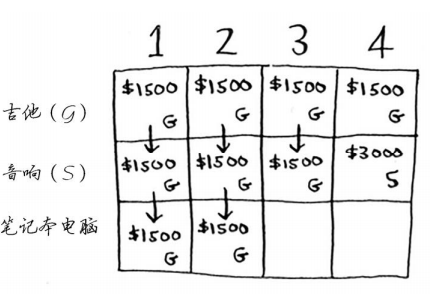
对于容量为3磅的背包,原来的最大价值为1500美元,但现在你可选择盗窃价值2000美元的笔记本电脑而不是吉他,这样新的最大价值将为2000美元!
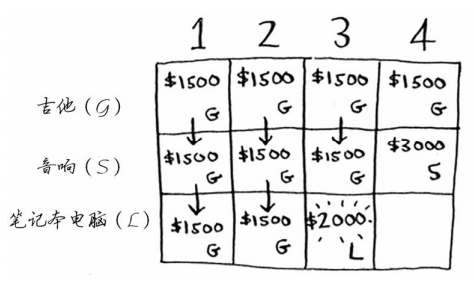
对于容量为4磅的背包,情况很有趣。这是非常重要的部分。当前的最大价值为3000美元,你可不偷音响,而偷笔记本电脑,但它只值2000美元。

价值没有原来高。但等一等,笔记本电脑的重量只有3磅,背包还有1磅的容量没用!
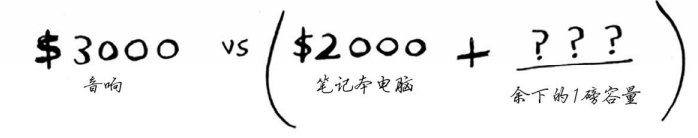
在1磅的容量中,可装入的商品的最大价值是多少呢?你之前计算过。
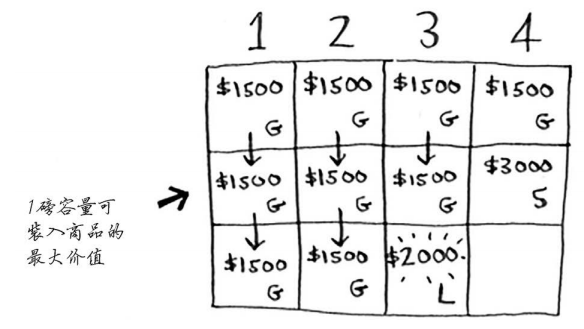
根据之前计算的最大价值可知,在1磅的容量中可装入吉他,价值1500美元。因此,你需要做如下比较。

你可能始终心存疑惑:为何计算小背包可装入的商品的最大价值呢?但愿你现在明白了其中的原因!余下了空间时,你可根据这些子问题的答案来确定余下的空间可装入哪些商品。笔记本电脑和吉他的总价值为3500美元,因此偷它们是更好的选择。最终的网格类似于下面这样。
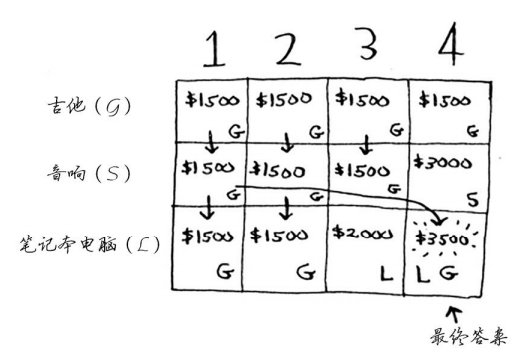
答案如下:将吉他和笔记本电脑装入背包时价值最高,为3500美元。
你可能认为,计算最后一个单元格的价值时,我使用了不同的公式。那是因为填充之前的单元格时,我故意避开了一些复杂的因素。其实,计算每个单元格的价值时,使用的公式都相同。这个公式如下。

为什么(i - 1):因为不减一可能会多次引用一个商品,如第一行的吉他。
你可以使用这个公式来计算每个单元格的价值,最终的网格将与前一个网格相同。现在你明白了为何要求解子问题吧?你可以合并两个子问题的解来得到更大问题的解。
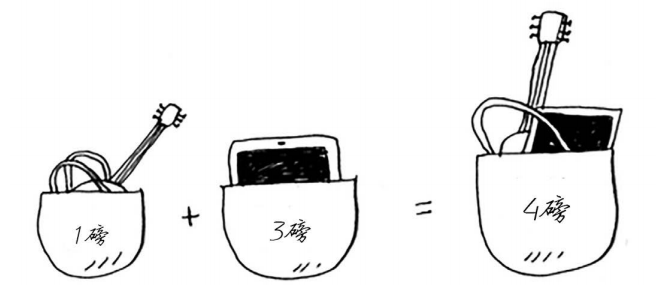
背包问题 FAQ
你可能还是觉得这像是变魔术。下面将回答一些常见的问题。
再增加一件商品将如何呢
假设你发现还有第四件商品可偷——一个iPhone!
此时需要重新执行前面所做的计算吗?不需要。别忘了,动态规划逐步计算最大价值。到目前为止,计算出的最大价值如下。
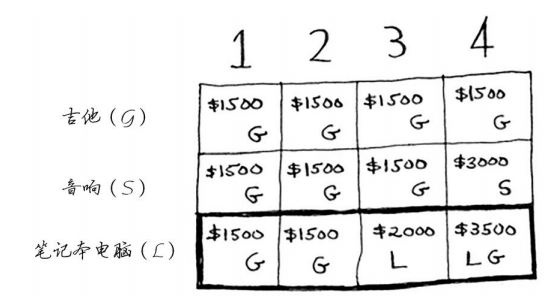

这意味着背包容量为4磅时,你最多可偷价值3500美元的商品。但这是以前的情况,下面再添加表示iPhone的行。
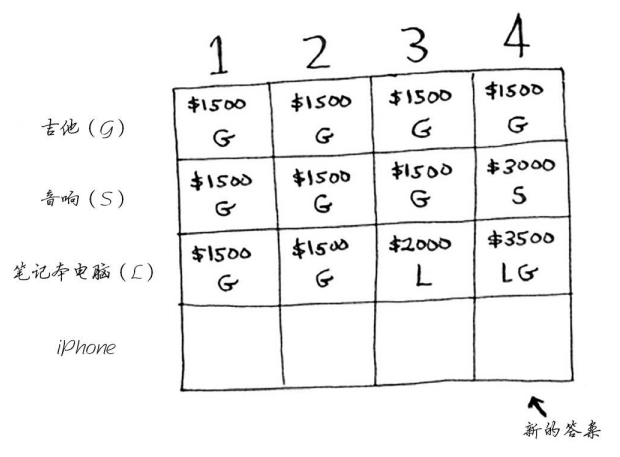
最大价值可能发生变化!请尝试填充这个新增的行,再接着往下读。
我们从第一个单元格开始。 iPhone可装入容量为1磅的背包。之前的最大价值为1500美元,但iPhone价值2000美元,因此该偷iPhone而不是吉他。
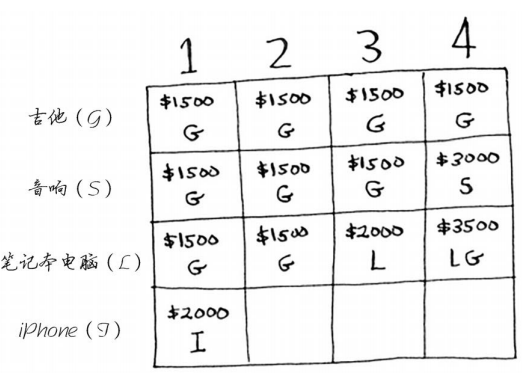
在下一个单元格中,你可装入iPhone和吉他。
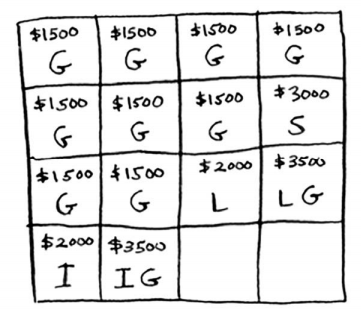
对于第三个单元格,也没有比装入iPhone和吉他更好的选择了。
对于最后一个单元格,情况比较有趣。当前的最大价值为3500美元,但你可偷iPhone,这将余下3磅的容量。

3磅容量的最大价值为2000美元!再加上iPhone价值2000美元,总价值为4000美元。新的最大价值诞生了!
最终的网格如下。
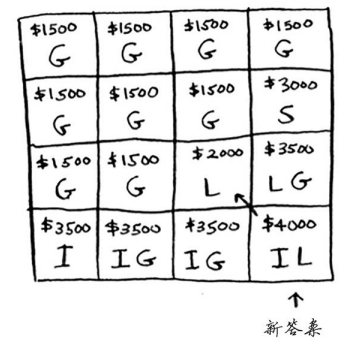
问题:沿着一列往下走时,最大价值有可能降低吗?
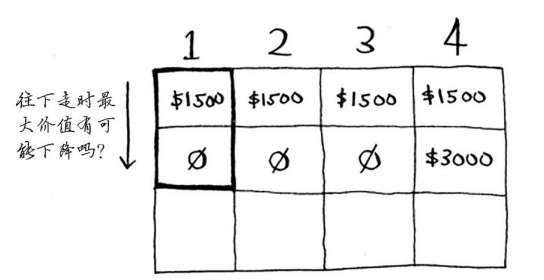
请找出这个问题的答案,再接着往下读。
答案:不可能。每次迭代时,你都存储当前的最大价值。最大价值不可能比以前低!
行的排列顺序发生变化时结果将如何
答案会随之变化吗?假设你按如下顺序填充各行:音响、笔记本电脑、吉他。网格将会是什么样的?请自己动手填充这个网格,再接着往下读。网格将类似于下面这样。
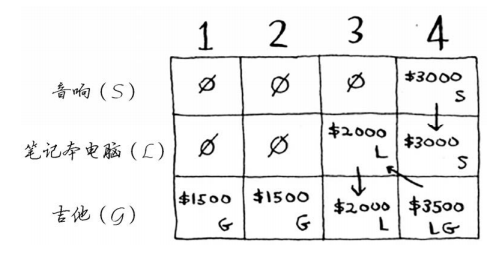
答案没有变化。也就是说,各行的排列顺序无关紧要。
旅游行程最优化
假设你要去伦敦度假,假期两天,但你想去游览的地方很多。你没法前往每个地方游览,因此你列个单子。

对于想去游览的每个名胜,都列出所需的时间以及你有多想去看看。根据这个清单,你能确定该去游览哪些名胜吗?
这也是一个背包问题!但约束条件不是背包的容量,而是有限的时间;不是决定该装入哪些商品,而是决定该去游览哪些名胜。请根据这个清单绘制动态规划网格,再接着往下读。
网格类似于下面这样。
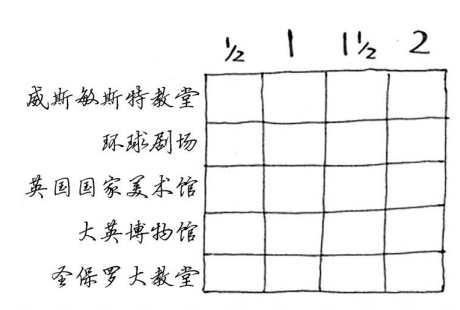
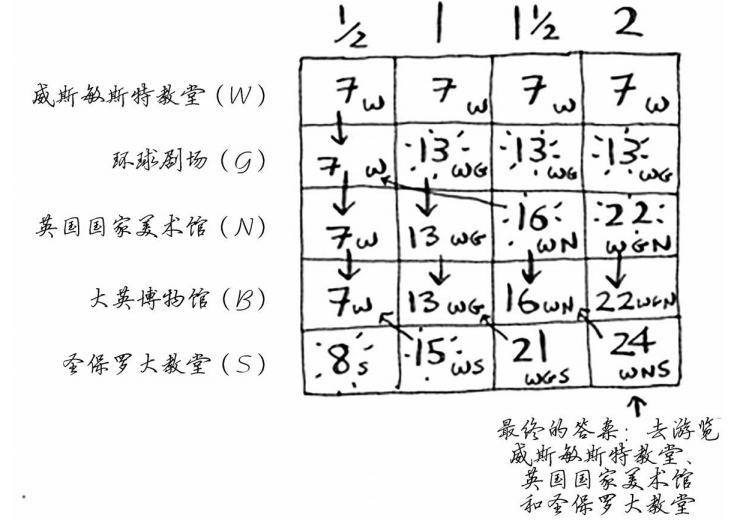
你画对了吗?请填充这个网格,决定该游览哪些名胜。答案如下。
处理相互依赖的情况
假设你还想去巴黎,因此在前述清单中又添加了几项。
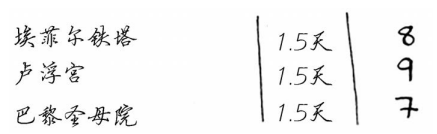
去这些地方游览需要很长时间,因为你先得从伦敦前往巴黎,这需要半天时间。如果这3个地方都去玩,是不是要4.5天呢?
不是的,因为不是去每个地方都得先从伦敦到巴黎。到达巴黎后,每个地方都只需1天时间。因此玩这3个地方需要的总时间为3.5天(半天从伦敦到巴黎,每个地方1天),而不是4.5天。
将埃菲尔铁塔加入“背包”后,卢浮宫将更“便宜”:只要1天时间,而不是1.5天。如何使用动态规划对这种情况建模呢?
没办法建模。动态规划功能强大,它能够解决子问题并使用这些答案来解决大问题。 但仅当每个子问题都是离散的,即不依赖于其他子问题时,动态规划才管用。 这意味着使用动态规划算法解决不了去巴黎玩的问题。
计算最终的解时会涉及两个以上的子背包吗
为获得前述背包问题的最优解,可能需要偷两件以上的商品。但根据动态规划算法的设计,最多只需合并两个子背包,即根本不会涉及两个以上的子背包。不过这些子背包可能又包含子背包。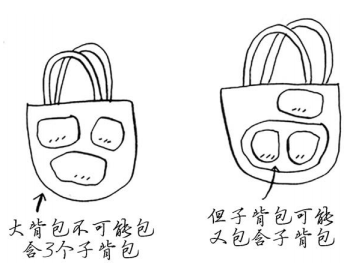
最优解可能导致背包没装满吗
完全可能。假设你还可以偷一颗钻石。
这颗钻石非常大,重达3.5磅,价值100万美元,比其他商品都值钱得多。你绝对应该把它给偷了!但当你这样做时,余下的容量只有0.5磅,别的什么都装不下。
最长公共子串
下面再来看一个例子。假设你管理着网站dictionary.com。用户在该网站输入单词时,你需要给出其定义。
但如果用户拼错了,你必须猜测他原本要输入的是什么单词。例如,Alex想查单词fish,但不小心输入了hish。在你的字典中,根本就没有
这样的单词,但有几个类似的单词。
在这个例子中,只有两个类似的单词,真是太小儿科了。实际上,类似的单词很可能有数千个。
Alex输入了hish,那他原本要输入的是fish还是vista呢?
如何将这个问题划分为子问题呢?你可能需要比较子串:不是比较hish和fish,而是先比较his和fis。每个单元格都将包含这两个子串的最长公共子串的长度。这也给你提供了线索,让你觉得坐标轴很可能是这两个单词。因此,网格可能类似于下面这样。
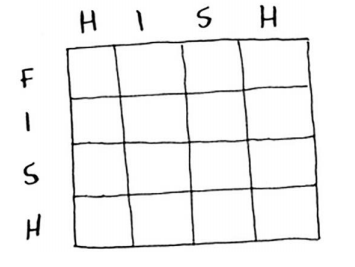
最长公共子序列之解决方案
最终的网格如下。
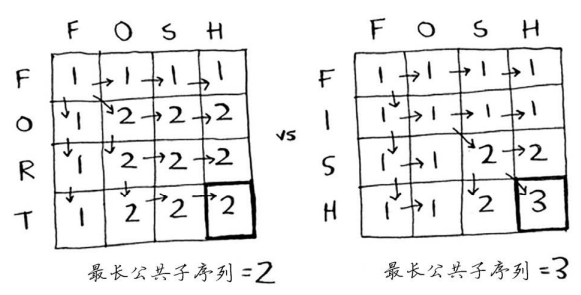
下面是填写各个单元格时使用的公式。
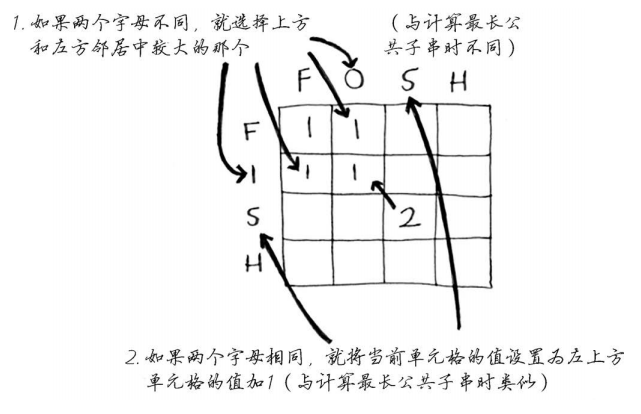
伪代码如下。
if (word_a[i] == word_b[j]) //两个字母相同
cell[i][j] = cell[i-1][j-1] + 1
else //两个字母不同
cell[i][j] = max(cell[i-1][j], cell[i][j-1])
通过前面的动态规划问题,你得到了哪些启示呢?
- 动态规划可帮助你在给定约束条件下找到最优解。在背包问题中,你必须在背包容量给定的情况下,偷到价值最高的商品。
- 在问题可分解为彼此独立且离散的子问题时,就可使用动态规划来解决。
要设计出动态规划解决方案可能很难,这正是本节要介绍的。下面是一些通用的小贴士。
- 每种动态规划解决方案都涉及网格。
- 单元格中的值通常就是你要优化的值。在前面的背包问题中,单元格的值为商品的价值。
- 每个单元格都是一个子问题,因此你应考虑如何将问题分成子问题,这有助于你找出网格的坐标轴。
简单小问题:=====================================
练习一:
给定一个有n(n>=1)个整数的序列,其中至少有一个正整数,求出该序列的最大序列和?
如:-2, 11, -4, 13, -5, -2:最大为(11,-4,13)20
用动态规划的思想:每一个前面的和都会影响后面的的和。所以做个列表
| -2 | 11 | -4 | 13 | -5 | -2 | |
| -2 | -2 | 9 | 5 | 18 | 13 | 11 |
| 11 | 11 | 7 | 20 | 15 | 13 | |
| -4 | -4 | 9 | 4 | 2 | ||
| 13 | 13 | 8 | 6 | |||
| -5 | -5 | -7 | ||||
| -2 | -2 |
实例代码:
#include<iostream>
#include<string.h>
#include<stdio.h>
#include <vector>
#include <time.h>
#include <stdlib.h>
#include <algorithm>
using namespace std;
int fun(vector<int> a)
{
int i = 0;
int j = 0;
int sum = 0;
int my_max = -256;
for (i = 0; i < a.size(); ++i) {
sum = 0;
for (j = i; j < a.size(); ++j) {
sum += a[j];
if (sum > my_max) my_max = sum;
}
}
return my_max;
}
int main()
{
int a[6] = {-2, 11, -4, 13, -5, -2};
vector<int> b(a, a+6);
cout<<fun(b);
return 1;
}
最后
以上就是无辜河马最近收集整理的关于算法学习(5):动态规划算法简单小问题:=====================================的全部内容,更多相关算法学习(5)内容请搜索靠谱客的其他文章。







![[经典面试题]排列组合专题](https://www.shuijiaxian.com/files_image/reation/bcimg13.png)
发表评论 取消回复