今天就来谈谈快速排序,我们也不详谈快速排序的时间复杂度,我们重点来分析一下快速排序的思想。
快速排序的思想十分简单,假设给定一个无序的数组,我们要从小到大排列,我们只需要完成以下几步
1、选取这个数组中的某一个元素为基准值,它的下标为基准点,这样数组就被分成了左右两个部分
2、将这个基准点左边的所有元素排好序(比这个基准值小)
3、将这个基准点右边的所有元素排好序(比这个基准值大)
4、将左半边和右半边进行合并
经过以上四步,数组中的所有元素都有序了。
当然了,这个只是一个非常初步的思想,并没有考虑得那么细。这时,我们会想,这个基准点怎么确定呢?这个排序究竟要执行几次比较呢?每次比较之后数组中的元素变化是如何的呢?
老实说哦,我也是刚具体接触这个算法。这个算法的实现可以使用递归,也可以使用非递归。今天就来说说递归吧。递归就好像数学中的递推公式,非常形象地描述了上面所说的四大步骤。快速排序递归实现的框架如下:
//定义程序支持的数据类型
#define Elemtype int
//快速排序算法的递归实现 a为待排序数组 l为要开始排序的下标 r为要结束排序的数组下标 (l,r)就是排序范围
void quickSort(Elemtype a[] , int l , int r)
{
//基准位置
int i;
//递归出口
if(r <= l)
{
return;
}
//确定基准点
i = partition(a,l,r);
//基准点左边排序
quickSort(a,l,i-1);
//基准点右边排序
quickSort(a,i+1,r);
}
我们先忽略递归出口 ,可以发现
1、有一个函数partion来确定基准点,这个基准点把数组分为左右两个部分(对应上面所说的步骤1)
2、将这个基准点(不包括)左边的所有元素排序,排序范围为l~i-1(对应上面所说的步骤2)
3、将这个基准点(不包括)右边的所有元素排序,排序范围为i+1~r(对应上面所说的步骤3)
最后我们再来看递归出口,我们知道,l表示排序开始的位置,r表示排序结束的位置,正常情况应该是开始的位置比结束位置小的,如果【开始的位置】 >【结束的位置】,那么就表示算法结束。
显然,使用递归实现的快速排序算法很好地反应了快速排序整体的思想框架。
注:这里我们是站在整体的角度来看待这个快速排序的思想框架,递归细分之后也相同,但是我感觉不用太纠结递归执行快速排序的具体流程以及每一步的数组变化,我们只要具体分析其中一部分就好。我记得我大一的时候老师说,递归就是我们指定好规则,剩下的交给计算机,根据我们所指定的规则,自己去探索。其实这个我也在慢慢体会,我也尝试去做快速排序的每一个部分的具体分析,发现真的好晕好晕。。。
接下来我们来看partition函数,这个函数就是快速排序的核心,它的功能是返回一个基准点,数据的比较和交换都在这个函数内完成,我们就1趟操作对这个函数的执行过程进行具体分析,剩下的以此类推就好。
我们打破以往博主直接上代码的传统,我今天将带大家一步一步将这个核心算法写出来。
1、假设我们有6个待排序的数1 3 2 8 0 6 存储在连续的内存空间中,数组名为a

2、我们不妨设最后一个元素,即a[5]的值为基准值
3、我们在前面提到,快速排序(从小到大)的思想要求,在基准点左边的数都要比基准点小,右边的数都要比基准点大,因此我们需要两个指针,分别指向待排序数组的头尾。又因为数组的最后一个元素被我们用作基准点,所以直接从它的前一个元素开始比较即可,所以,我们采用先自减,再比较,即【--j】的方式。为了统一,我们同样在左边比较时,也采用【++i】的形式,因此,我们的两个指针begin和end在初始化时,应分别指向-1位置,和第5个位置。

4、结合在基准点左边数据要比基准点小,右边的要比基准点大的思想,我们可以很容易地写出一个大致的代码。因为我们不像冒泡排序那样能够知道整个排序过程要执行几次,因此采用死循环。
//快速排序的核心,返回基准点
int partition(Elemtype a[] , int l , int r)
{
//i,j为begin和end的初始位置
int i = l - 1;
int j = r;
//基准值
Elemtype x = a[r];
//因为不知要执行几次,所以使用死循环
while(1)
{
while(a[++i] < x);//假设数组已有序,那么,在基准值左边的所有元素的值<基准值
while(a[--j] > x);//假设数组已有序,那么,在基准值右边的所有元素的值>基准值
}
}那么,接下来我们就根据这个大致的框架来分析一下什么时候结束循环,什么时候要交换数据,又是返回谁的下标作为基准点的问题。
5、我们根据算法框架,先进入了第一个while循环。我们知道,只有当数组中有比基准元素大于或者等于时,循环退出。在执行第一个循环时,既然是要把基准点左边排好序,所以应该是从头开始遍历。最好情况是在x左边的所有元素都比x来的小,当且仅当begin即i指针所指元素与基准元素x重合时,循环结束。根据本题,我们可以得到如下的一个排序过程
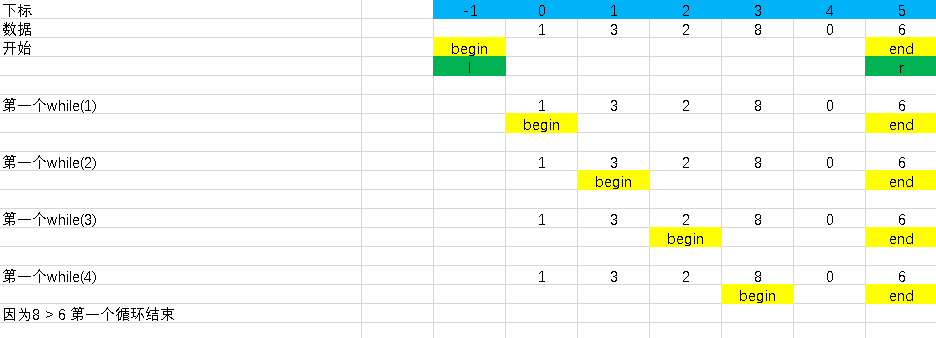
由图可知,第一个循环能够自动退出。
6、退出第一个循环后,我们便进入了第二个循环。既然第一个循环是对数组左半边进行排序,那么第二个循环就是对数组的右半边进行排序了。依然以元素x为基准,根据前面的思想,数组右半边的元素应该都比x来的大。因此,我们不妨从数组右边开始往左遍历,只要end指针,即j指针所指的元素比x来的大就往前进,比x小就退出。所以,我们又能够得到如下的一个排序过程。
7、第二个循环退出后,如果死循环未退出,在重新进入第一个循环之前,我们需要对下标为begin和end所指的元素进行交换,这一步非常重要。
假象一下,如果不进行交换,那么在下一次循环结束之后,begin会停留在6元素,end会停留在2元素,如下图

无论说把6安置在begin或者end位置,都不能保证数组中以6为基准,左半边的元素比6小,右边的元素比6大了。
根据此时数组中的情况(交换值之后的数组),我们会想,此时能不能将基准元素6交换到到数组中了呢?不难发现,如果把6交换在begin的位置,那么6之后的元素为8、0,不符合思想要求;如果把6交换到end的位置,我们发现在这个例子中是能保证以6为基准的数组中左半边的值比6小,右半边的值比6大的。但是考虑一下8 5 7 2 6 3这个情况。在第一次退出两个while循环后,begin与end的指针位置是这样的:

可以发现,如果把3交换到end的位置,那么就完全错乱了,是吧~所以,我们退出死循环的条件构想得并不准确,
因此,我们并不能退出这个死循环。必须从第一个while循环重新开始。

8、第一个循环退出后,顺理成章进入第二个while循环

9、此时,我们发现。只要把基准元素6与begin指针所指的元素8进行交换,刚好以6为基准的数组左边的所有元素都比6来的小,右边的元素都比6来的大。我们终于找到了基准元素的交换位置。找到交换位置后,我们就不需要再进行死循环了,因此,死循环退出的条件为end > begin,对应到程序中,就是i > j。我们的程序完善如下:
//快速排序的核心,返回基准点
int partition(Elemtype a[] , int l , int r)
{
//i,j为begin和end的初始位置
int i = l - 1;
int j = r;
//基准值
Elemtype x = a[r];
//因为不知要执行几次,所以使用死循环
while(1)
{
while(a[++i] < x);//假设数组已有序,那么,在基准值左边的所有元素的值<基准值
while(a[--j] > x);//假设数组已有序,那么,在基准值右边的所有元素的值>基准值
if(i > j)
{
break;
}
swap(&a[i],&a[j]);
}
}
10、退出死循环之后,我们就找到了交换点,存于begin指针,即i指针中。我们只需要将基准元素6,与begin指针所指的元素8进行交换就行,即a[i] = a[r],返回基准点
//快速排序的核心,返回基准点
int partition(Elemtype a[] , int l , int r)
{
//i,j为begin和end的初始位置
int i = l - 1;
int j = r;
//基准值
Elemtype x = a[r];
//因为不知要执行几次,所以使用死循环
while(1)
{
while(a[++i] < x);//假设数组已有序,那么,在基准值左边的所有元素的值<基准值
while(a[--j] > x);//假设数组已有序,那么,在基准值右边的所有元素的值>基准值
if(i > j)
{
break;
}
swap(&a[i],&a[j]);
}
swap(&a[i],&a[r]);
return i;
}
好了,经过以上10步,我们就能大致写好partition函数了。但是,这个函数并不健壮,还存在以下问题:
1、假设数组右边都已有序,即都比基准值大,那么第二个循环就无法退出了。
2、退出死循环的条件i能不能等于j 即 i==j 或begin == end
我们先解决第一个问题
如果数组右边的值都比x来的大,说明这个x是这个数组中最小的元素,应该放置在数组头,因此,假如我们从后向前遍历的指针end(即j)已经到达数组头(我们传入的begin,即l)时,就该退出循环。
我们再来解读第二个问题
如果i==j,即begin == end,说明起始指针已经与结束指针相遇。如果死循环继续进行,那么先执行的是第一个while循环,begin指针向右推进。那么问题来了,begin指针一旦向右推进,那么它所指元素的下标已经大于end了,这样再执行第二个循环已经没有意义了,等于说begin指针已经越到了end指针所管辖的范围。因此,当begin == end(即i == j),就是基准元素x应该要插入的位置,应当退出死循环。
由此,我们知道,begin指针只管辖数组的左半边,end指针只管辖数组的右半边,而基准元素x,就是它们的“国界”。
所以,完整的partition函数如下
//快速排序的核心,返回基准点
int partition(Elemtype a[] , int l , int r)
{
//i,j为begin和end的初始位置
int i = l - 1;
int j = r;
//基准值
Elemtype x = a[r];
//因为不知要执行几次,所以使用死循环
while(1)
{
while(a[++i] < x);//假设数组已有序,那么,在基准值左边的所有元素的值<基准值
while(a[--j] > x){if(j == l) break;};//假设数组已有序,那么,在基准值右边的所有元素的值>基准值
if(i >= j)
{
break;
}
swap(&a[i],&a[j]);
}
swap(&a[i],&a[r]);
return i;
}
附上swap函数的定义
void swap(int *a , int *b)//把b的值给a,把a的值给b
{
int t = *a;
*a = *b;
*b = t;
}
最后是完整代码
#include <stdio.h>
//定义程序支持的数据类型
#define Elemtype int
void swap(int *a , int *b);
//快速排序的核心,返回基准点
int partition(Elemtype a[] , int l , int r);
//快速排序算法的递归实现 a为待排序数组 l为要开始排序的下标 r为要结束排序的数组下标 (l,r)就是排序范围
void quickSort(Elemtype a[] , int l , int r)
{
//基准位置
int i;
//递归出口
if(r <= l)
{
return;
}
//确定基准点
i = partition(a,l,r);
//基准点左边排序
quickSort(a,l,i-1);
//基准点右边排序
quickSort(a,i+1,r);
}
//快速排序的核心,返回基准点
int partition(Elemtype a[] , int l , int r)
{
//i,j为begin和end的初始位置
int i = l - 1;
int j = r;
//基准值
Elemtype x = a[r];
//因为不知要执行几次,所以使用死循环
while(1)
{
while(a[++i] < x);//假设数组已有序,那么,在基准值左边的所有元素的值<基准值
while(a[--j] > x){if(j == l) break;};//假设数组已有序,那么,在基准值右边的所有元素的值>基准值
if(i >= j)
{
break;
}
swap(&a[i],&a[j]);
}
swap(&a[i],&a[r]);
return i;
}
void swap(Elemtype *a , Elemtype *b)
{
//b的值交换到a , a的值交换到b
Elemtype t = *a;
*a = *b;
*b = t;
}
int main()
{
Elemtype a[6] = {1,2,3,0,6,8};
int i = 0;
quickSort(a,0,5);
for(; i<6 ; i++)
{
printf("%d ",a[i]);
}
printf("n");
return 0;
}
运行结果如下
最后简单说一下快速排序的时间复杂度为O(nlogn)
最后
以上就是漂亮鸭子最近收集整理的关于【算法】快速排序算法(递归实现 从小到大排列) 排序范围(0~n-1) n为数组元素个数的全部内容,更多相关【算法】快速排序算法(递归实现内容请搜索靠谱客的其他文章。






![[经典面试题]排列组合专题](https://www.shuijiaxian.com/files_image/reation/bcimg13.png)

发表评论 取消回复