动态规划

将待求解问题分解成若干个子问题，分阶段求解子问题，前一阶段子问题的解成为求后续阶段子问题的解的计算信息，最后用这些子问题的最优解构造出原问题的最优解。
适合用动态规划求解的问题的特征
(1) 子问题重叠性
①子问题重复
②子问题的解在下一阶段决
策中，延续子问题多次使用
(2) 最优子结构
一个问题的最优解包含着它的子问题的最优解
基本步骤
(1) 找出最优解的性质，并刻画其结构特征。
(2) 按最优解的性质，划分子问题及演算的阶段，递推求解最优解。
(3) 以自底向上或自顶向下的记忆化方法 ( 备忘录法 ) 计算出最优值。
(4) 根据每阶段推算出的局部最优解，构造出全局最优解。

例题1

有一个数塔，结点中数字为其权值，按自顶向下（或自底向上）方式行走，经过的每一个结点，可以选择向左或向右走，到达底（或顶部），求一条自顶向下（或自底向上）的路径，所经过结点权值和最大。

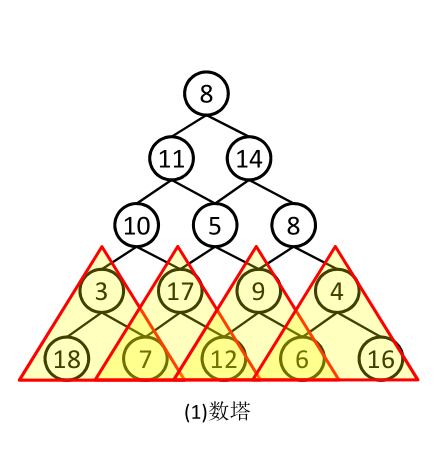
【思路】：设dp[i][j]是在i行j列所达到的最大值。
{ d p [ i ] [ j ] = m a x { d p [ i + 1 ] [ j ] , d p [ i + 1 ] [ j + 1 ] } + a [ i ] [ j ] d p [ n ] [ j ] = a [ n ] [ j ] left{ begin{array}{lr} dp[i][j] = max{dp[i+1][j],dp[i+1][j+1]}+a[i][j]\ dp[n][j] = a[n][j] end{array} right. {dp[i][j]=max{dp[i+1][j],dp[i+1][j+1]}+a[i][j]dp[n][j]=a[n][j]​
自底向上进行查找。

#include <stdio.h>
#define N 100
int dp[N][N];
int a[N][N];
int n;
/*
input
5
8
11 14
10 5 8
3 17 9 4
18 7 12 6 16

output
max = 58
path:
(1,1)  a[0][0]=8   dp[0][0]=58
(2,1)  a[1][0]=11  dp[1][0]=50
(3,1)  a[2][0]=10  dp[2][0]=39
(4,2)  a[3][1]=17  dp[3][1]=29
(5,3)  a[4][2]=12  dp[4][2]=12

*/
int max(int a,int b){
	return a>b?a:b;
}
int main(int argc, char const *argv[])
{
	int n;
	scanf("%d",&n);
	for (int i = 0;i<n;++i){
		for (int j=0;j<=i;++j){
			scanf("%d",&a[i][j]);
		}
	}
	for(int i=n-1;i>=0;--i){
		for(int j=0;j<=i;++j){
			if(i==n-1){
				dp[i][j] = a[i][j];
			}
			else{
				dp[i][j] = max(dp[i+1][j],dp[i+1][j+1])+a[i][j];
			}
		}
	}
	int sum = dp[0][0];
	printf("max = %dn", dp[0][0]);
	printf("path:n");
	for (int i = 0; i < n; ++i)
	{
		for (int j = 0; j <= i; ++j)
		{
			if(dp[i][j]==sum){
				sum = sum - a[i][j];
				printf("(%d,%d)  a[%d][%d]=%d  dp[%d][%d]=%dn",i+1,j+1,i,j,a[i][j],i,j,dp[i][j]);
				break;
			}
		}
	}
	return 0;
}

例题2

设有 $n$ 万元钱，投资 $m$ 个项目，将 $x_i$ 万元钱投入第 $i$ 个项产生的效益为 $f_i(x_i)，i=1,2,\dots ,m$ 。请问如何分配这 $n$ 万元钱，使得投资的总效益最高？

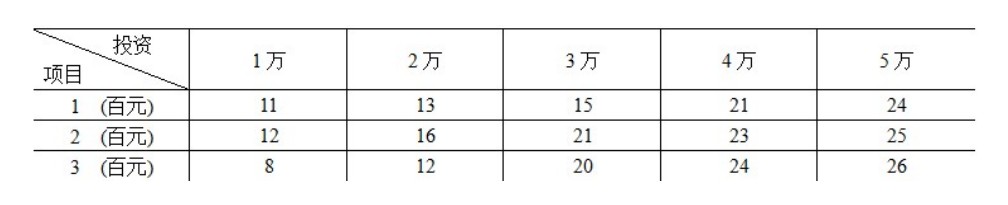
【思路】：
设题目中不同投资不同项目对应不同回报的数组为a，例子中所示的数组。
首先有dp数组dp[m][n],dp[i][j]代表投资j万元，只考虑前i个项目所获的最大收益。money[m][n]为投资分配金额，money[i][j]表示共有j万元，只考虑前i项目，获得最大回报时，对应第i项的投资。
$$\{\begin{array}{lr}dp[i][j]=a[i][j],money[i][j]=j& i=1,j\in [0,n]\\ dp[i][j]=max(dp[i-1][k]+a[i][j-k])& i>1,k\in [0,j]\\ money[i][j]=j-k& 对应最大值的j和k\end{array}$$

#include<stdio.h>
#define N 100
/*
input
5 3
11 13 15 21 24
12 16 21 23 25
8  12 20 24 26

output
最大收益为43万
第3个项目投资3万
第2个项目投资1万
第1个项目投资1万

*/
int m,n;
int a[N][N];
int dp[N][N];
int money[N][N];
int main(int argc, char const *argv[])
{
	scanf("%d%d",&n,&m);
	for (int i=1;i<=m;++i){
		for (int j=1;j<=n;++j){
			scanf("%d",&a[i][j]);
		}
	}
	for (int i=0;i<=n;++i){
		dp[1][i] = a[1][i];
		money[1][i] = i;
	}
	for (int i=2;i<=m;++i){
		for (int j=0;j<=n;++j){
			int max = 0;
			int mon = 0;
			for (int k=0;k<=j;++k){
				if(max<dp[i-1][k]+a[i][j-k]){
					max = dp[i-1][k]+a[i][j-k];
					mon = j-k;
				}
			}
			dp[i][j] = max;
			money[i][j] = mon;
		}
	}
	printf("最大收益为%d万n",dp[m][n]);
	int mon = n;
	for (int i=m;i>=1;--i){
		printf("第%d个项目投资%d万n",i,money[i][mon]);
		mon = mon - money[i][mon];
	}
	return 0;
}

例题3

【动态规划求解0-1背包问题】

【思路】：
存储方面：设结构体

struct{
	int w,v;
}a[n];

构建dp数组(dp[n][w])。
dp[i][j]代表只考虑前i个物品，在重量最多为j的条件下，所能达到的放入物品价值的最大量。
{ d p = { 0 } 初 始 化 d p [ 1 ] [ j ] = a [ 1 ] . v j ≥ a [ 1 ] . w d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j − a [ i ] . w ] + a [ i ] . v , d p [ i − 1 ] [ j ] ) j > = a [ i ] . w d p [ i ] [ j ] = d p [ i − 1 ] [ j ] j < a [ i ] . w left{ begin{array}{lr} dp = {0} &初始化\ dp[1][j] = a[1].v&jgeq a[1].w\ dp[i][j] = max(dp[i-1][j-a[i].w]+a[i].v,dp[i-1][j])& j>=a[i].w\ dp[i][j] = dp[i-1][j]& j<a[i].w end{array} right. ⎩⎪⎪⎨⎪⎪⎧​dp={0}dp[1][j]=a[1].vdp[i][j]=max(dp[i−1][j−a[i].w]+a[i].v,dp[i−1][j])dp[i][j]=dp[i−1][j]​初始化j≥a[1].wj>=a[i].wj<a[i].w​
在实际编程时dp数组其实可以降维。

#include <stdio.h>
#include <algorithm>
using namespace std;
#define N 100
/*
input
4 5
2 12
1 10
3 20
2 15

output
最大价值为37
重量为3,价值为20的物品：不选上
重量为2,价值为15的物品：选上
重量为2,价值为12的物品：选上
重量为1,价值为10的物品：选上

*/

struct good
{
	int v;
	int w;
}a[N];
int dp[N];
int x[N][N];//记录最优解
int m,n;
int max(int a,int b){
	return a>b?a:b;
}
int main(int argc, char const *argv[])
{
	scanf("%d%d",&n,&m);
	for(int i=0;i<n;++i)
		scanf("%d%d",&a[i].w,&a[i].v);
	for (int i = 0; i < m; ++i)
	{
		if(a[0].w<=i) {dp[i] = a[0].v,x[0][i]=1;};
	}
	for (int i = 1; i < n; ++i)
	{
		for (int j = m; j >= 0; --j)
		{
			int tmp = dp[j];
			if(j>=a[i].w)
				dp[j] = max(dp[j-a[i].w]+a[i].v,dp[j]);
			if(dp[j]==tmp)
				x[i][j] = 0;
			else
				x[i][j] = 1;
		}
	}
	printf("最大价值为%dn", dp[m]);
	int w = m;
	for(int i=n-1;i>=0;i--){
		printf("重量为%d,价值为%d的物品：%sn",a[i].w,a[i].v,x[i][w]==1?"选上":"不选上");
		if(x[i][w]==1) w = w - a[i].w;
	}
	return 0;
}

例题4

【矩阵连乘问题】

【思路】首先，默认这n个矩阵可以矩阵相乘，则有前一个矩阵的列数等于后一个矩阵的行数。我们设：r[1] 代表第 1 个矩阵的行数，r[i] 代表第 i-1 个矩阵的列数（i>=2）,dp[i][j] 表示从第j个矩阵开始,作i次连乘所需乘法次数最小值，即为 a[j]… .a[j+i-1] 连乘积乘法次数的最小值。
其中有一个隐含条件：j到j+i-1乘得的矩阵行数为r[j]，列数为r[j+i]
状态转移方程

$$\{\begin{array}{lr}dp[1][j]=0& j\in [1,n]\\ dp[2][j]=r[j]\ast r[j+1]\ast r[j+2]& j\in [1,n-1]\\ dp[i][j]=min(dp[k+1][j]& \\ +dp[i-k-1][j+k+1]& \\ +r[j]\ast r[j+k+1]\ast r[j+i])& \\ i\in [3,n],j\in [1,n-i+1],k\in [0,i-2](对应dp[i][j])& \end{array}$$

//矩阵连乘问题的非递归解法
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<string.h>
#include<time.h>
using namespace std;
const int N=100;
const int inf=1000000;
/*
input
4
3 2
2 2
2 1
1 2

output
n个输入矩阵为
3 0 
4 1 
2 1 

2 1 
2 0 

1 
3 

0 4 

最小乘法次数：16
乘法次序为
(1*(2*3))*4最终乘得矩阵为
0 60 
0 88 
0 48 

*/
struct arr
{
	int w;
	int h;
	int v[N][N];
};
arr a[N];
int com[N][N];
int r[N+1];
int dp[N][N];
void printarr(arr res){
	for (int i=1;i<=res.h;++i)
	{
		for (int j=1;j<=res.w;++j)
		{
			printf("%d ", res.v[i][j]);
		}
		printf("n");
	}
}

void print(int i,int j)
{
	if (com[i][j]-i>0){
		printf("(");
		print(i,com[i][j]);
		printf(")");
		if(com[i][j]+1==j)
			printf("*");
	}
	else{
		printf("%d*", i);
	}
	if (com[i][j]+1<j)
	{
		printf("(");
		print(com[i][j]+1,j);
		printf(")");
	}
	else{
		printf("%d", j);
	}
}
arr getres(int i,int j)
{
	arr a1,a2,a3;
	if (com[i][j]-i>0){
		// printf("(%d-%d)*",i,com[i][j]);
		a1=getres(i,com[i][j]);
	}
	else{
		a1=a[i];
	}
	if (com[i][j]+1<j)
	{
		a2=getres(com[i][j]+1,j);
	}
	else{
		a2=a[j];
	}
	a3.w=a2.w,a3.h=a1.h;
	for (int i=1;i<=a3.h;++i)
	{
		for(int j=1;j<=a3.w;++j)
		{
			a3.v[i][j]=0;
			for (int k=1;k<=a1.w;++k)
			{
				a3.v[i][j]=a3.v[i][j]+a1.v[i][k]*a2.v[k][j];
			}
		}
	}
	return a3;
}
//输入矩阵个数n，以及n个矩阵的行列数，矩阵内容随机数自动生成
int main()
{
	int n;//共有n个矩阵
	srand((int)time(0));  // 产生随机种子  把0换成NULL也行
	scanf("%d",&n);
	for(int i=1;i<=n;++i)
		for(int j=1;j<=n;++j)
			dp[i][j]=inf;//顺便进行dp数组的初始化
	for (int i=1;i<=n;++i){
		scanf("%d %d",&a[i].h,&a[i].w);
		if (i==1)
			r[i]=a[i].h;
		r[i+1]=a[i].w;
		for(int j=1;j<=a[i].h;++j)
		{
			for(int k=1;k<=a[i].w;++k)
			{
				// scanf("%d",&a[i].v[j][k]);
				a[i].v[j][k]=rand()%5;
			}
		}
	}
	// 初始化dp数组,和com数组非递归做法
	//和老师的略有不同 这里的dp[i][j]代表i个数进行连乘，
	//从第j个矩阵开始连乘的最小相乘次数。
	for (int i=1;i<=n-1;++i){
		dp[2][i]=r[i]*r[i+1]*r[i+2];
		dp[1][i]=0;
		com[i][i+1]=i;
	}
	dp[1][n]=0;
	for(int i=3;i<=n;++i)  //i==3表示3个数进行连乘
	{
		for(int j=1;j<=n-i+1;++j)
		{
			for (int k=0;k<=i-2;++k)
			{
				int tmp=dp[i][j];
				dp[i][j]=min(dp[k+1][j]+dp[i-k-1][j+k+1]+r[j]*r[j+k+1]*r[j+i],dp[i][j]);
				if (tmp!=dp[i][j])
					com[j][j+i-1]=j+k;
			}
		}
	}
	printf("n个输入矩阵为n");
	for(int i=1;i<=n;++i){
		printarr(a[i]);
		printf("n");
	}
	printf("最小乘法次数：%dn",dp[n][1]);
	printf("乘法次序为n");
	print(1,n);
	arr res=getres(1,n);
	printf("最终乘得矩阵为n");
	printarr(res);
	return 0;
}

例题5

最大子段和

好了，写到 这里算法系列博客生涯就结束了，突然有点茫然了。。。
参考资料：张小东老师ppt

最后

以上就是含糊睫毛为你收集整理的【算法】动态规划动态规划的全部内容，希望文章能够帮你解决【算法】动态规划动态规划所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。