三角矩阵
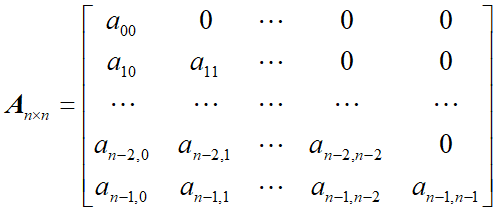
三角矩阵的常用压缩方式有两种:
- 线性压缩
- 使用三角形的二维数组压缩
线性压缩存储三角矩阵
下三角矩阵:
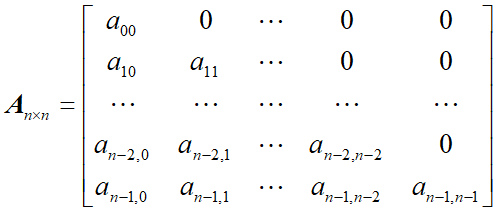
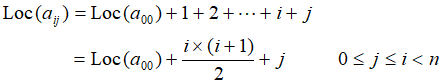

上三角矩阵:
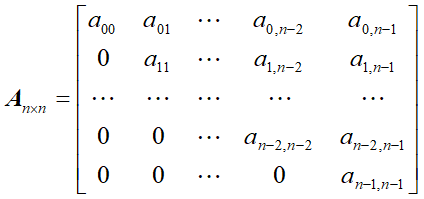
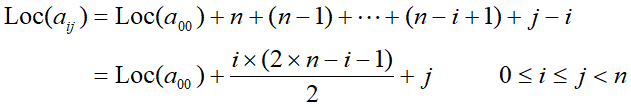

以下三角矩阵的线性压缩存储为例,进行实现:
package pers.zhang.array;
/**
* @author zhang
* @date 2020/1/19 - 13:34
*
* 下三角矩阵线性压缩存储
*/
public class DownTriangleMatrix {
//下三角矩阵的阶数
private int rows;
//存储矩阵元素的一维数组
private int element[];
//构造rows阶下三角矩阵
public DownTriangleMatrix(int rows){
if(rows <= 0)
throw new IllegalArgumentException("矩阵行数非正数:" + rows);
this.rows = rows;
//rows阶下三角矩阵需要存储rows*(rows+1)/2个元素
this.element = new int[rows * (rows + 1) / 2];
}
//构造rows阶下三角矩阵,初值由mat提供,mat按行主序顺序存储rows阶下三角矩阵元素
public DownTriangleMatrix(int rows, int mat[]){
this(rows);
int n = element.length <= mat.length ? element.length : mat.length;
for (int i = 0; i < n; i++)//mat元素不足时补0,忽略多余元素
this.element[i] = mat[i];
}
//深拷贝
public DownTriangleMatrix(DownTriangleMatrix mat){
this(mat.rows, mat.element);
}
//返回矩阵第i行第j列元素值,O(1)
public int get(int i, int j) {
if (i < 0 || i >= rows || j < 0 || j >= rows)
throw new IndexOutOfBoundsException("矩阵元素的行或列序号越界");
return i < j ? 0 : element[i * (i + 1) / 2 + j];//按线性压缩存储地址寻找矩阵元素
}
//设置矩阵第i行第j列元素值为value,O(1)
public void set(int i, int j, int value){
if (i < 0 || i >= rows || j < 0 || j >= rows)
throw new IndexOutOfBoundsException("矩阵元素的行或列序号越界");
this.element[i * (i + 1) / 2 + j] = value;
}
//返回下三角矩阵所有元素的描述字符串,行主序遍历
public String toString(){
String str =" 下三角矩阵" + this.getClass().getName() + "(" + this.rows + "阶):n";
for (int i = 0; i < this.rows; i++){
for (int j = 0; j < this.rows; j++)
str += String.format("%4d", this.get(i,j));
str += "n";
}
return str;
}
//当前下三角矩阵与mat矩阵相加,this+=mat,各对应元素相加,改变当前矩阵
public void add(DownTriangleMatrix mat){
if (this.rows != mat.rows)
throw new IllegalArgumentException("两个矩阵阶数不同,不能相加");
for (int i = 0; i < this.element.length; i++)
this.element[i] += mat.element[i];
}
//返回当前矩阵与mat相加后的矩阵,=this+mat,各对应元素相加,不改变当前矩阵
public DownTriangleMatrix plus(DownTriangleMatrix mat){
DownTriangleMatrix matc = new DownTriangleMatrix(this);//深拷贝
matc.add(mat);
return matc; //返回对象引用
}
//比较两个同阶矩阵是否相等
public boolean equals(Object obj){
if (this == obj)
return true;
if (!(obj instanceof DownTriangleMatrix))
return false;
DownTriangleMatrix mat=(DownTriangleMatrix)obj;
if (this.rows != mat.rows)
return false;
for (int i = 0; i < this.element.length; i++)
if (this.element[i] != mat.element[i]) //比较对应元素是否相等
return false;
return true;
}
}
测试:
package pers.zhang.array;
/**
* @author zhang
* @date 2020/1/19 - 14:00
*/
public class DownTriangleMatrix_ex {
public static void main(String args[])
{
int m1[]={1,2,3,4,5,6,7,8,9,10,11,12};
DownTriangleMatrix mata=new DownTriangleMatrix(4,m1); //忽略m1多余元素
System.out.print("A"+mata.toString());
int m2[]={1,0,1,0,0,1};
DownTriangleMatrix matb=new DownTriangleMatrix(4,m2); //m2元素不足时补0
matb.set(3,3,1);
System.out.print("B"+matb.toString());
DownTriangleMatrix matc = mata.plus(matb);
System.out.print("C=A+B"+mata.plus(matb).toString());
mata.add(matb);
System.out.println("A+=B"+mata.toString());
System.out.println("C.equals(A)?"+matc.equals(mata));
}
}
/*
A 下三角矩阵pers.zhang.array.DownTriangleMatrix(4阶):
1 0 0 0
2 3 0 0
4 5 6 0
7 8 9 10
B 下三角矩阵pers.zhang.array.DownTriangleMatrix(4阶):
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
C=A+B 下三角矩阵pers.zhang.array.DownTriangleMatrix(4阶):
2 0 0 0
2 4 0 0
4 5 7 0
7 8 9 11
A+=B 下三角矩阵pers.zhang.array.DownTriangleMatrix(4阶):
2 0 0 0
2 4 0 0
4 5 7 0
7 8 9 11
C.equals(A)?true
*/
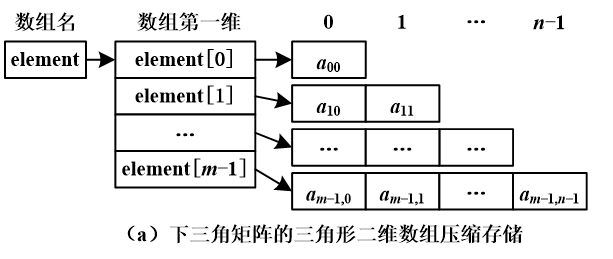
使用三角形的二维数组压缩存储三角矩阵
下三角矩阵:
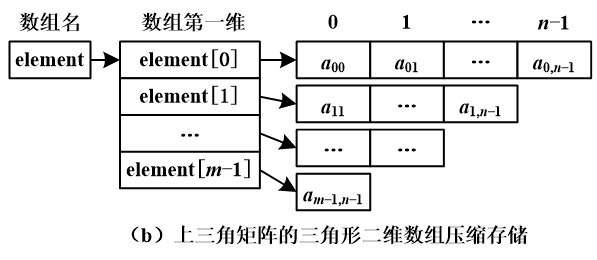
上三角矩阵:
实现:
package pers.zhang.array;
/**
* @author zhang
* @date 2020/1/19 - 14:17
*
* 三角矩阵的二维数组压缩存储
*/
public class TriangleMatrix {
//上或下三角矩阵标识
private boolean up;
//三角形的二维数组存储矩阵非零元素
private int element[][];
//构造rows阶零矩阵,up为true时上三角矩阵
public TriangleMatrix(int rows, boolean up){
this.up = up;
this.element = new int[rows][];//若rows<0,Java将抛出负数组长度异常NegativeArraySizeException
if (up)//上三角矩阵
for (int i = 0; i< this.element.length; i++)
this.element[i] = new int[rows-i];//数组元素初值为0
else //下三角矩阵
for (int i = 0; i < this.element.length; i++)
this.element[i] = new int[i+1];
}
//构造rows阶矩阵,由二维数组mat提供元素
public TriangleMatrix(int rows, boolean up, int mat[][]){
this(rows, up);
for (int i = 0; i < mat.length && i < this.element.length; i++) //mat元素不足时补0,忽略多余元素
for (int j = 0; j < mat[i].length && j < this.element[i].length; j++)
this.element[i][j] = mat[i][j];
}
//深拷贝
public TriangleMatrix(TriangleMatrix mat){
this(mat.element.length, mat.up, mat.element);
}
//返回矩阵第i行第j列元素值,O(1)
public int get(int i, int j){
if (up)
return i>j ? 0 : this.element[i][j-i];
else
return i<j ? 0 : this.element[i][j];//若i、j下标越界,Java将抛出数组下标越界异常ArrayIndexOutOfBoundsException
}
//设置矩阵第i行第j列的元素值为value,O(1)
public void set(int i, int j, int value){
if (up)
this.element[i][j - i] = value;
else
this.element[i][j] = value;
}
//行主序遍历,访问矩阵全部元素
public String toString(){
String str = " " + this.getClass().getName() + "(" + this.element.length + "阶):n";
for (int i = 0; i < this.element.length; i++){
for (int j = 0; j < this.element.length; j++)
str += String.format("%4d", this.get(i,j));
str += "n";
}
return str;
}
//当前矩阵与mat矩阵相加,this+=mat,各对应元素相加,改变当前矩阵
public void add(TriangleMatrix mat){
if (this.element.length != mat.element.length)
throw new IllegalArgumentException("两个矩阵阶数不同,不能相加"); //抛出无效参数异常
if (this.up != mat.up)
throw new IllegalArgumentException("该类不支持上三角矩阵与下三角矩阵相加");
for (int i = 0; i < this.element.length; i++)
for (int j = 0; j < this.element[i].length; j++)
this.element[i][j] += mat.element[i][j];
}
//返回当前矩阵与mat相加后的矩阵,不改变当前矩阵,=this+mat,各对应元素相加
public TriangleMatrix plus(TriangleMatrix mat){
TriangleMatrix matc = new TriangleMatrix(this); //深拷贝
matc.add(mat);
return matc; //返回对象引用
}
//比较两个同阶矩阵是否相等
@Override
public boolean equals(Object obj){
if (this == obj)
return true;
if (!(obj instanceof TriangleMatrix))
return false;
TriangleMatrix mat = (TriangleMatrix)obj;
if (this.element.length != mat.element.length || this.up!=mat.up)
return false;
for (int i = 0; i < this.element.length; i++)
for (int j = 0; j < this.element[i].length; j++)
if (this.element[i][j] != mat.element[i][j]) //比较对应元素是否相等
return false;
return true;
}
//返回当前矩阵的转置矩阵
public TriangleMatrix transpose(){
TriangleMatrix trans = new TriangleMatrix(this.element.length, !this.up);//构造零矩阵
if (up) //上三角矩阵转置为下三角矩阵
for (int i = 0; i < this.element.length; i++)
for (int j = 0; j < this.element[i].length; j++)
trans.element[j + i][i] = this.element[i][j];
else //下三角矩阵转置为上三角矩阵
for (int i = 0; i < this.element.length; i++)
for (int j = 0; j < this.element[i].length; j++)
trans.element[j][i - j] = this.element[i][j];
return trans; //返回对象引用
}
}
测试:
package pers.zhang.array;
/**
* @author zhang
* @date 2020/1/19 - 15:54
*/
public class TriangleMatrix_ex {
public static void main(String args[])
{
int m1[][]={{1,2,3,4},{5,6,7},{8,9},{10}};
TriangleMatrix mata=new TriangleMatrix(4,true,m1); //矩阵对象,初值不足时自动补0,忽略多余元素
System.out.print("A"+mata.toString());
TriangleMatrix matb=new TriangleMatrix(4,true);
matb.set(0,0,1);
matb.set(0,3,1);
matb.set(1,1,1);
matb.set(3,3,1);
System.out.print("B"+matb.toString());
TriangleMatrix matc = mata.plus(matb);
System.out.print("C=A+B"+matc.toString());
mata.add(matb);
System.out.print("A+=B"+mata.toString());
System.out.println("C.equals(A)?"+matc.equals(mata));
int m2[][]={{1},{2,3},{4,5,6},{7,8,9,10}};
TriangleMatrix matd=new TriangleMatrix(4,false,m2); //矩阵对象,初值不足时自动补0,忽略多余元素
System.out.print("nD"+matd.toString());
TriangleMatrix mate=new TriangleMatrix(4,false);
mate.set(0,0,1);
mate.set(1,1,1);
mate.set(3,0,1);
mate.set(3,3,1);
System.out.print("E"+mate.toString());
TriangleMatrix matf = matd.plus(mate);
System.out.print("F=D+E"+matf.toString());
matd.add(mate);
System.out.print("D+=E"+matd.toString());
System.out.println("F.equals(D)?"+matc.equals(mata));
System.out.println("B.equals(E)?"+matb.equals(mate)+"n");
TriangleMatrix matg = matb.transpose();
System.out.print("B的转置矩阵G"+matg.toString());
System.out.println("G.equals(E)?"+matg.equals(mate)+"n");
TriangleMatrix math = mate.transpose();
System.out.print("E的转置矩阵H"+math.toString());
System.out.println("H.equals(B)?"+math.equals(matb));
}
}
/*
程序运行结果如下:
A TriangleMatrix(4阶):
1 2 3 4
0 5 6 7
0 0 8 9
0 0 0 10
B TriangleMatrix(4阶):
1 0 0 1
0 1 0 0
0 0 0 0
0 0 0 1
C=A+B TriangleMatrix(4阶):
2 2 3 5
0 6 6 7
0 0 8 9
0 0 0 11
A+=B TriangleMatrix(4阶):
2 2 3 5
0 6 6 7
0 0 8 9
0 0 0 11
C.equals(A)?true
D TriangleMatrix(4阶):
1 0 0 0
2 3 0 0
4 5 6 0
7 8 9 10
E TriangleMatrix(4阶):
1 0 0 0
0 1 0 0
0 0 0 0
1 0 0 1
F=D+E TriangleMatrix(4阶):
2 0 0 0
2 4 0 0
4 5 6 0
8 8 9 11
D+=E TriangleMatrix(4阶):
2 0 0 0
2 4 0 0
4 5 6 0
8 8 9 11
F.equals(D)?true
B.equals(E)?false
B的转置矩阵G TriangleMatrix(4阶):
1 0 0 0
0 1 0 0
0 0 0 0
1 0 0 1
G.equals(E)?true
E的转置矩阵H TriangleMatrix(4阶):
1 0 0 1
0 1 0 0
0 0 0 0
0 0 0 1
H.equals(B)?true
*/
最后
以上就是满意纸飞机最近收集整理的关于数据结构--三角矩阵的压缩存储的全部内容,更多相关数据结构--三角矩阵内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。
![数据结构----三角矩阵压缩存储中下标的计算一.三角矩阵的概念二.压缩原理三.矩阵坐标[i,j]转换为一维数组下标K的方法](https://www.shuijiaxian.com/files_image/reation/bcimg12.png)







发表评论 取消回复