c语言人脸疲劳检测,关键点提取：face_recognition、疲劳检测、人脸校准、人脸数据库...

余弦类似度/余弦类似性

1.余弦类似度

经过计算两个向量的夹角余弦值来评估他们之间的类似度。

夹角余弦值的取值范围在[-1,1]，任何角度的余弦值都在-1到1之间。

两个向量之间的夹角角度的余弦值(余弦类似度的值)肯定两个向量是否大体指向相同的方向，与向量的的长度无关，仅仅与向量的指向方向相关。

两个向量之间夹角为0°的话，余弦值(余弦类似度的值)为1，表明两个向量的指向方向相同。

两个向量之间夹角为90°的话，余弦值(余弦类似度的值)为0，表明两个向量的指向方向垂直。

两个向量之间夹角为180°的话，余弦值(余弦类似度的值)为-1，表明两个向量的指向方向相反。

余弦类似度一般用于正空间，所以给出的值为0到1之间，一般用于文本挖掘中的文件比较。

一个向量空间中两个向量夹角间的余弦值做为衡量两个个体之间差别的大小，余弦值接近1，夹角趋于0，代表两个向量越类似；

余弦值接近于0，夹角趋于90度，代表两个向量越不类似。

2.余弦类似度，又称为余弦类似性，是经过计算两个向量的夹角余弦值来评估他们的类似度。

余弦类似度将向量根据坐标值，绘制到向量空间中，如最多见的二维空间。

余弦类似度用于评估两个向量的夹角的类似度。

余弦值的范围在[-1,1]之间，值越趋近于1，表明两个向量的方向越接近；越趋近于-1，他们的方向越相反；接近于0，表示两个向量近乎于正交。

最多见的应用就是计算文本类似度。将两个文本根据他们词，创建两个向量，计算这两个向量的余弦值，就能够知道两个文本在统计学方法中他们的类似度状况。

实践证实，这是一个很是有效的方法。

3.余弦类似性经过测量两个向量的夹角的余弦值来度量它们之间的类似性。0度角的余弦值是1，而其余任何角度的余弦值都不大于1；而且其最小值是-1。

从而两个向量之间的角度的余弦值肯定两个向量是否大体指向相同的方向。两个向量有相同的指向时，余弦类似度的值为1；

两个向量夹角为90°时，余弦类似度的值为0；两个向量指向彻底相反的方向时，余弦类似度的值为-1。

这结果是与向量的长度无关的，仅仅与向量的指向方向相关。余弦类似度一般用于正空间，所以给出的值为-1到1之间。

注意这上下界对任何维度的向量空间中都适用，并且余弦类似性最经常使用于高维正空间。

例如在信息检索中，每一个词项被赋予不一样的维度，而一个维度由一个向量表示，其各个维度上的值对应于该词项在文档中出现的频率。

余弦类似度所以能够给出两篇文档在其主题方面的类似度。

另外，它一般用于文本挖掘中的文件比较。此外，在数据挖掘领域中，会用到它来度量集群内部的凝聚力。

4.两个向量间的余弦值能够经过使用欧几里得点积公式求出：

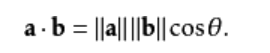
给定两个属性向量，A和B，其他弦类似性θ由点积和向量长度给出，以下所示：

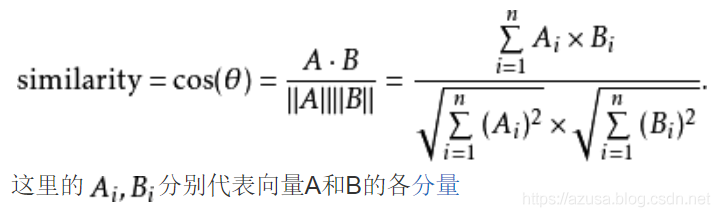
给出的类似性范围从-1到1：-1意味着两个向量指向的方向正好截然相反，1表示它们的指向是彻底相同的，0一般表示它们之间是独立的，

而在这之间的值则表示中间的类似性或相异性。

对于文本匹配，属性向量A和B一般是文档中的词频向量。余弦类似性，能够被看做是在比较过程当中把文件长度正规化的方法。

在信息检索的状况下，因为一个词的频率(TF-IDF权)不能为负数，因此这两个文档的余弦类似性范围从0到1。而且，两个词的频率向量之间的角度不能大于90°。

5.角类似性

“余弦类似性”一词有时也被用来表示另外一个系数，尽管最多见的是像上述定义那样的。透过使用相同计算方式获得的类似性，

向量之间的规范化角度能够做为一个范围在[0,1]上的有界类似性函数，从上述定义的类似性计算以下：

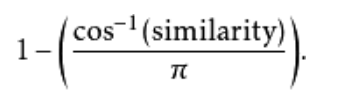
这式子适用于向量系数能够为正或负的状况。或者，用如下式子计算

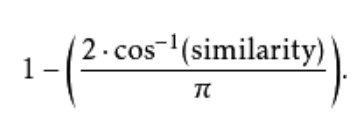
这式子适用于向量系数总为正的状况。

虽然“余弦类似性”一词有时会用来表示这个角距离，但实际上不多这样说，由于角度的余弦值只是做为一种计算角度的简便方法而被用到，

自己并非意思的一部分。角类似系数的优势是，看成为一个差别系数(从1减去它)时，产生的函数是一个严格距离度量，

而对于第一种意义的“余弦类似性”则否则。然而，对于大多数的用途，这不是一个重要的性质。若对于某些状况下，

只有一组向量之间的类似性或距离的相对顺序是重要的，那么无论是使用哪一个函数，所得出的顺序都是同样的。

6.与“Tanimoto”系数的混淆

有时，余弦类似性会跟一种特殊形式的、有着相似代数形式的类似系数相混淆：

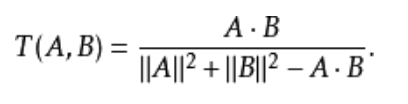
事实上，这个代数形式是首先被Tanimoto定义，做为在所比较集合由位元向量表示时计算其Jaccard系数的方法。

虽然这公式也能够扩展到向量，它具备和余弦类似性颇为不一样的性质，而且除了形式类似外便没有什么关系。

7.Ochiai系数

这个系数在生物学中也叫Ochiai系数，或Ochiai-Barkman系数：

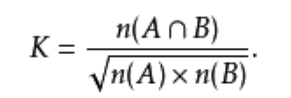
这里A和B是集合，n(A)是A的元素个数。若是集合由位元向量所表明，那么可看到Ochiai系数跟余弦类似性是等同的。

8.计算余弦值推导

1.余弦函数在三角形中的计算公式为

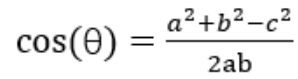
a和b表明两个向量(向量是在空间中具备大小和方向的量，在数据计量中表示带箭头的线段)

2.二维空间的余弦函数的公式：将a、b两个向量二维化，经过余弦定理与二维空间结合，便可推导出来二维空间下计算两个向量的余弦类似性公式。

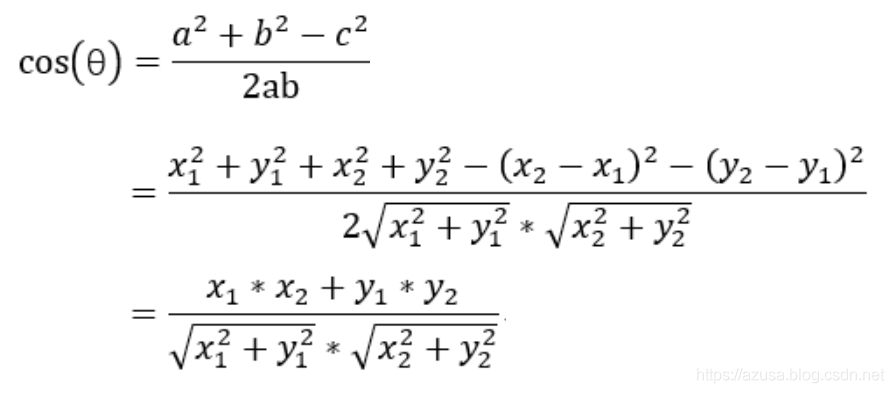
上图中向量a用坐标(x1,y1)表示，向量b用坐标(x2,y2)表示。向量a和向量b在直角坐标中的长度分别为

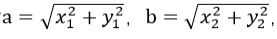
向量a和向量b之间的距离咱们用向量c表示,那么向量c在直角坐标系中的长度为

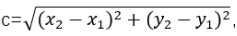
将a，b，c带入三角函数的公式中便获得了直角坐标系中向量表示的三角形的余弦函数。

二维向量图和余弦定理的结合：

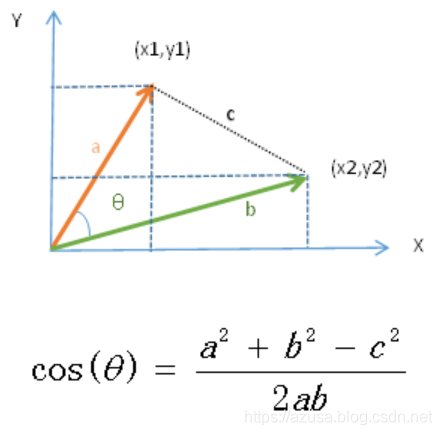
3.多维空间的余弦函数的公式

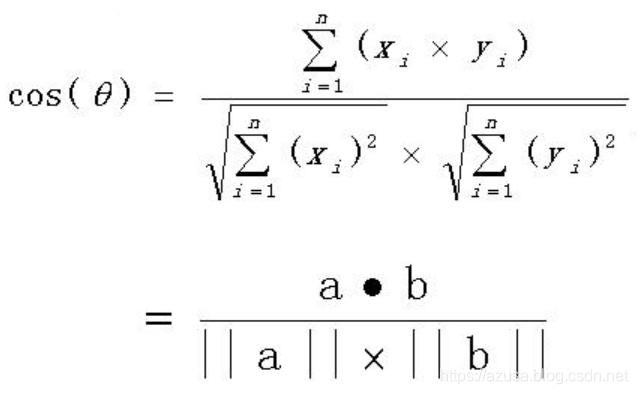
9.计算余弦类似度例子一

1.余弦类似度量：计算个体间的类似度。

类似度越小，距离越大。类似度越大，距离越小。

2.假设有3个物品，item1，item2和item3，用向量表示分别为：item1[1,1,0,0,1]，item2[0,0,1,2,1]，item3[0,0,1,2,0]。

3.用欧式距离公式计算item一、itme2之间的距离，以及item2和item3之间的距离，分别是：

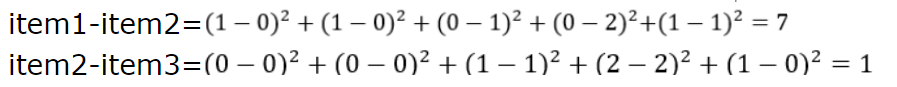
4.用余弦函数计算item1和item2夹角间的余弦值为：

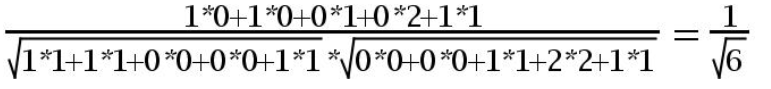
5.用余弦函数计算item2和item3夹角间的余弦值为：

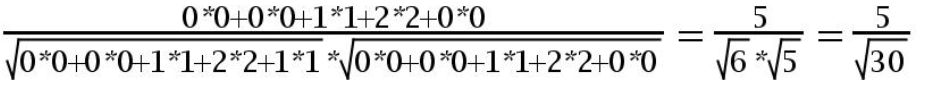
6.由此可得出item1和item2类似度小，两个之间的距离大(距离为7)，item2和itme3类似度大，二者之间的距离小(距离为1)。

7.余弦类似度算法：

一个向量空间中两个向量夹角间的余弦值做为衡量两个个体之间差别的大小，余弦值接近1，夹角趋于0，代表两个向量越类似；

余弦值接近于0，夹角趋于90度，代表两个向量越不类似。

10.计算余弦类似度例子二

1.使用余弦类似度计算两段文本的类似度。

思路：一、对原文进行jieba中文分词；

二、set中去重后存储全部词，并使用dict字段存储set中元素值(key)和索引值(value)；

三、中文分词进行编码：每一个中文分词转换为出如今set中的索引值；

四、词频向量化：即计算每一个分词出现的次数，经过oneHot编码对分词进行编码来计算词频，从而获得两个句子分别的词频向量；

五、根据余弦类似度的公式分别计算出两个句子的的类似度，即计算两个句子分别的词频向量之间夹角的余弦值，值越大类似度越高。

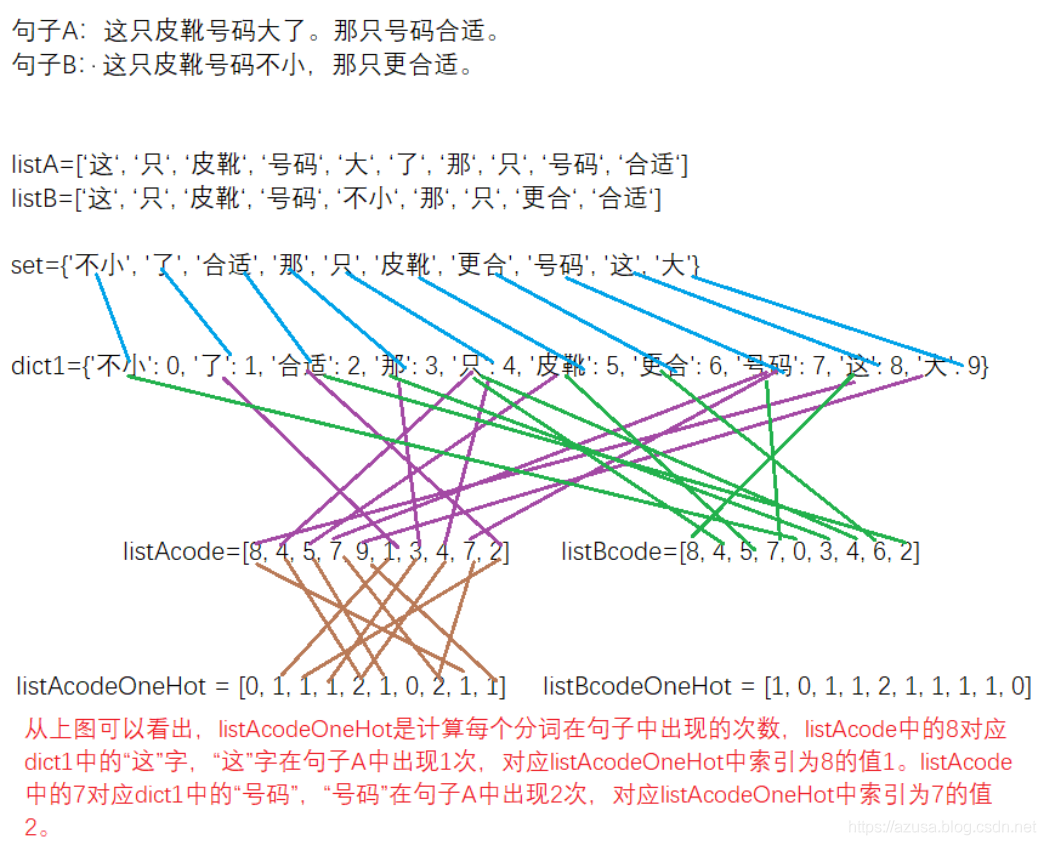
2.原文句子A：这只皮靴号码大了。那只号码合适。

原文句子B：这只皮靴号码不小，那只更合适。

3.分词

使用jieba分词对上面两个原文句子分词后，分别获得两个列表：

listA=['这', '只', '皮靴', '号码', '大', '了', '那', '只', '号码', '合适']

listB=['这', '只', '皮靴', '号码', '不小', '那', '只','更合', '合适']

3.列出全部词，将listA和listB放在一个set中，set中去重后获得：

set={'不小', '了', '合适', '那', '只', '皮靴', '更合', '号码', '这', '大'}

将上述set转换为dict，key为set中的词，value为set中词出现的索引位置。

dict1={'不小': 0, '了': 1, '合适': 2, '那': 3, '只': 4, '皮靴': 5, '更合': 6, '号码': 7, '这': 8, '大': 9}，

能够看出“不小”这个词在set中排第1，下标为0。

4.将listA和listB中的中文分词进行编码，将每一个中文分词转换为出如今set中的索引值，转换后为：

listAcode=[8, 4, 5, 7, 9, 1, 3, 4, 7, 2]

listBcode=[8, 4, 5, 7, 0, 3, 4, 6, 2]

咱们来分析listAcode，结合dict1，得知元素值8对应的字是“这”，元素值4对应的字是“只”，元素值9对应的字是“大”，就是句子A和句子B转换为用set中的索引值来表示。

5.对listAcode和listBcode进行oneHot编码，就是计算每一个分词出现的次数。

词频向量化：即计算每一个分词出现的次数，经过oneHot编码对分词进行编码来计算词频，从而获得两个句子分别的词频向量。

oneHot编号后获得的结果以下：

listAcodeOneHot = [0, 1, 1, 1, 2, 1, 0, 2, 1, 1]

listBcodeOneHot = [1, 0, 1, 1, 2, 1, 1, 1, 1, 0]

6.根据余弦类似度的公式分别计算出两个句子的的类似度，即计算两个句子分别的词频向量之间夹角的余弦值，值越大类似度越高。

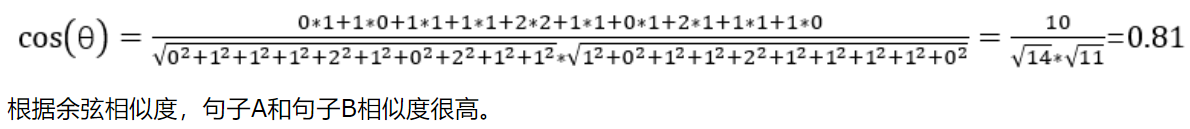
7.流程图

11.实现余弦类似度的代码

import jieba

import math

s1 = '这只皮靴号码大了。那只号码合适'

s1_cut = [i for i in jieba.cut(s1, cut_all=True) if i != '']

s2 = '这只皮靴号码不小，那只更合适'

s2_cut = [i for i in jieba.cut(s2, cut_all=True) if i != '']

print(s1_cut) #['这', '只', '皮靴', '号码', '大', '了', '那', '只', '号码', '合适']

print(s2_cut)#['这', '只', '皮靴', '号码', '不小', '那', '只', '更合', '合适']

#两个set分别对中文切割后的数组元素进行去重，而后两个set联合union放到一块儿组成一个新的set

word_set = set(s1_cut).union(set(s2_cut))

print(word_set)#{'只', '合适', '不小', '更合', '号码', '皮靴', '这', '了', '大', '那'}

word_dict = dict()

i = 0

#构建dict字典中的key为set中的每一个中文单词，value为set中的该中文单词的索引值

for word in word_set:

word_dict[word] = i

i += 1

print(word_dict) #{'只': 0, '合适': 1, '不小': 2, '更合': 3, '号码': 4, '皮靴': 5, '这': 6, '了': 7, '大': 8, '那': 9}

#把原文中每一个中文单词做为key对应的从dict字典中取出对应的value，值为set中的该中文单词的索引值

s1_cut_code = [word_dict[word] for word in s1_cut]

print(s1_cut_code) #[6, 0, 5, 4, 8, 7, 9, 0, 4, 1]

#把原文中每一个中文单词做为key对应的从dict字典中取出对应的value，值为set中的该中文单词的索引值

s2_cut_code = [word_dict[word] for word in s2_cut]

print(s2_cut_code) #[6, 0, 5, 4, 2, 9, 0, 3, 1]

#从新建立一个新的和dict字典键值对数量相同的初始化值为0的数组

s1_cut_code = [0]*len(word_dict)

#oneHot编码：计算原文中每一个中文分词出现的次数，即能获得原文句子的词频向量

#根据原文中相同中文单词出现的重复次数记录到新数组中，出现次数要记录到的索引位置为该中文单词在set中索引值，或者说dict字典中的该中文单词做为key对应的value

for word in s1_cut:

s1_cut_code[word_dict[word]]+=1

print(s1_cut_code)#[2, 1, 0, 0, 2, 1, 1, 1, 1, 1]

#从新建立一个新的和dict字典键值对数量相同的初始化值为0的数组

s2_cut_code = [0]*len(word_dict)

#oneHot编码：计算原文中每一个中文分词出现的次数，即能获得原文句子的词频向量

#根据原文中相同中文单词出现的重复次数记录到新数组中，出现次数要记录到的索引位置为该中文单词在set中索引值，或者说dict字典中的该中文单词做为key对应的value

for word in s2_cut:

s2_cut_code[word_dict[word]]+=1

print(s2_cut_code)#[2, 1, 1, 1, 1, 1, 1, 0, 0, 1]

# 计算余弦类似度

sum = 0

sq1 = 0

sq2 = 0

#经过计算余弦值的公式cos(θ)= (x1*x2 + y1*y2) / sqrt(pow(x1,2)+pow(y1,2)) * sqrt(pow(x2,2)+pow(y2,2))

#pow(x,y)函数用于求 x 的 y 次方

for i in range(len(s1_cut_code)):

#计算(x1*x2 + y1*y2)：x1*x2或y1*y2均表明词频向量s1_cut_code中的元素值 乘以 词频向量s2_cut_code中的元素值

sum += s1_cut_code[i] * s2_cut_code[i]

#计算pow(x1,2)+pow(y1,2)：表明求词频向量s1_cut_code中的每一个元素值的2次方

sq1 += pow(s1_cut_code[i], 2)

#计算pow(x2,2)+pow(y2,2)：表明求词频向量s2_cut_code中的每一个元素值的2次方

sq2 += pow(s2_cut_code[i], 2)

try:

#sqrt() 计算平方根，即开平方

#round(浮点数x,四舍五入要保留的小数位) 方法返回浮点数x的四舍五入值。

#计算出余弦值的结果cos(θ)= (x1*x2 + y1*y2) / sqrt(pow(x1,2)+pow(y1,2)) * sqrt(pow(x2,2)+pow(y2,2))

result = round(float(sum) / (math.sqrt(sq1) * math.sqrt(sq2)), 2)

except ZeroDivisionError:

result = 0.0

print(result) #0.81