非对称TSP问题（asymmetric travelling salesman problem）与对称TSP问题的转换

小伙伴们有没有这样的经验：在上课10分钟前从寝室骑车飞奔向教学楼时，寝室到教学楼的路非常挤；而这个时候，如果有东西落在寝室，从教学楼往寝室飞奔时的车道却很空。换句话说，在一些场合，从点$i$到点$j$的行驶时间和从点$j$到点$i$的行驶时间是不同的。这个现象当然不会被学者们忽视。这就是我们今天要介绍的非对称类问题（asymmetric）。

非对称TSP与对称TSP

在我们以往介绍的TSP问题和VRP问题中，算例给出的通常是客户点的二维坐标，两点之间的距离通过欧拉距离（平方和开根号）计算，因此两点间不同向的边距离是相同的。因此，我们在设计算子时可以对一些边进行“翻转”，例如“1→2→3→4→5”翻转为“1→4→3→2→5”，这个时候由于距离的对称性，“2→3→4”与“4→3→2”两段路径的距离是相同的，不需要重新计算。但在我们今天介绍的非对称TSP问题中，由于反向后距离发生变化，这两段路径的距离将发生改变，这种去重优化的方法就失效了。

1983年学者Roy Jonker 和 Ton Volgenant 提出了一种将非对称TSP问题转换为对称TSP问题的方法。通过这种方法，我们可以将非对称TSP问题转化为对称TSP问题，然后使用适合对称问题的算法求解该问题，而不是重新设计算法。

转化方法

Roy和Ton通过扩充原问题graph的规模的方式，在新的graph上求解对称TSP问题，然后将新解转化为旧问题的解。

通过以下操作，将一个非对称TSP问题的距离矩阵$C$转化为对称TSP问题的距离矩阵$\tilde{C}$（${\tilde{C}}^T=\tilde{C}$）：

1. 令$\bar{C}=C$，其中${\bar{c}}_{ii}=-M(i\in N)$。（M是一个很大的数，N为节点集合）
2. 令$U$为一个n维方阵，对 $\forall i,j\in N$ 令 $u_{ij}=\infty$
3. 令$\tilde{\mathbf{C}}=\left[\begin{array}{ll}U& {\overline{\mathbf{C}}}^T\\ \overline{\mathbf{C}}& \mathbf{U}\end{array}\right]$

得到的矩阵$\mathbf{C}$就是新的对称TSP问题的距离矩阵。可以看出，这个矩阵是一个2n*2n规模的方阵，新的节点集为 { 1 , 2 , … , n , n + 1 , … , 2 n } {1,2, ldots, n, n+1, ldots, 2 n} {1,2,…,n,n+1,…,2n}。

求解这个新的TSP问题得到的最优解必定是以下形式（或其对称形式）：

$i_1\to \left(i_1+n\right)\to i_2\to \left(i_2+n\right)\to \cdots \to i_n\to \left(i_n+n\right)\to i_1$

其中$i_k\in N$。

也就是说，新问题的最优解中，每一个节点必定指向到它对应的拓展出的节点，而每一个新的节点必定指向原先图中的某个节点。该解对应的原问题的最优解即为：

$i_1\to i_2\to \cdots \to i_n\to i_1$

深入理解

看了前文的转化方法，是不是感觉特别简单呢？只需要通过一些简单的矩阵操作得到新的距离矩阵，路径的转化也非常简单，只需要取奇数位的节点编号即可。

在原论文中作者提出一个定理：新问题的最优解必定对应一个原问题的最优解，并没有给出完整证明。事实上转化的思维也很简单，这里小编给大家文字证明一下。

在矩阵操作的第一步得到$\bar{C}=C$的过程中，${\bar{c}}_{ii}=-M$在新矩阵$\mathbf{C}$中实际上对应了节点$i_k$和$i_k+n$。所以在新问题的最优解中，必须尽可能多的包含$i_k\to \left(i_k+n\right)$这类边。由于一个节点只能访问一次，所以这类边最多存在n条。由于矩阵$U$的每一个数都是无穷大，因此不存在$\left(i_{k1}+n\right)\to \left(i_{k2}+n\right)$以及$i_{k1}\to i_{k2}$这两种边，因此新解中剩下的边只能是$\left(i_{k1}+n\right)\to i_{k2}$的形式了。

由于$\left(i_{k1}+n\right)\to i_{k2}$的距离与$i_{k1}\to i_{k2}$的距离相等，并且每个新问题最优解中必定存在n条距离为-M的边，因此新的目标函数相当于原问题的目标函数减去一个常数（n*M），因此原问题与新问题等价。

小编解释的可能有点绕，不过原理并不复杂，相信同学们能够思考清楚。

代码分享

为了验证方法的准确性，小编基于干货 | JAVA调用cplex求解一个TSP模型详解中的TSP模型代码编写了将非对称TSP问题转化对称TSP问题进行求解的代码。（代码下载见文末）事实上，上述文章提到的模型不需要改动也可以作为非对称TSP问题的模型，只需要修改输入为矩阵形式，一样可以求解。小编简单测试了“直接通过模型求解”和“转化为对称问题通过模型求解”两种形式，验证转化方法的正确性：

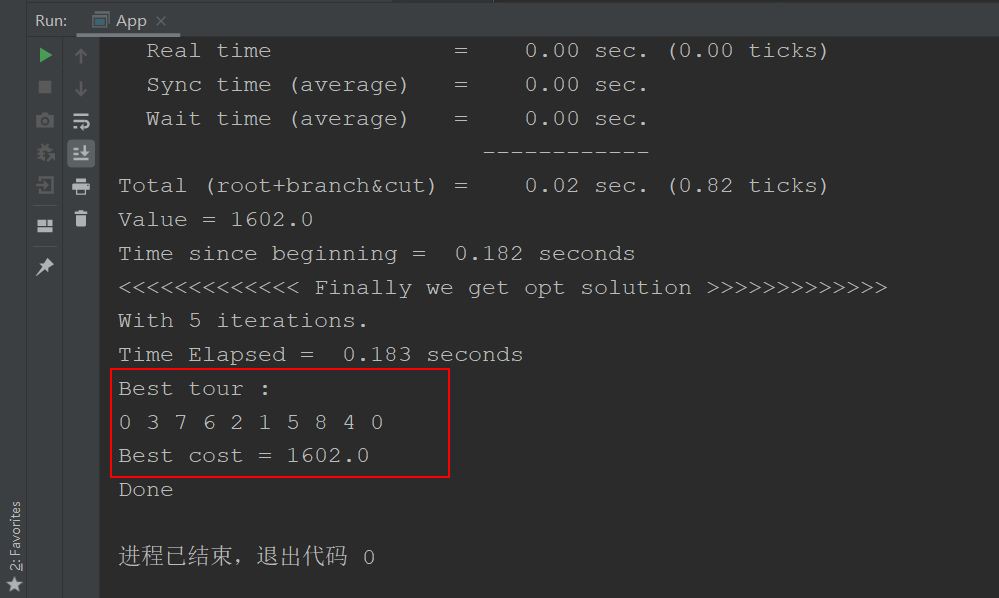
直接求解模型结果：

转化为对称问题求解模型结果：

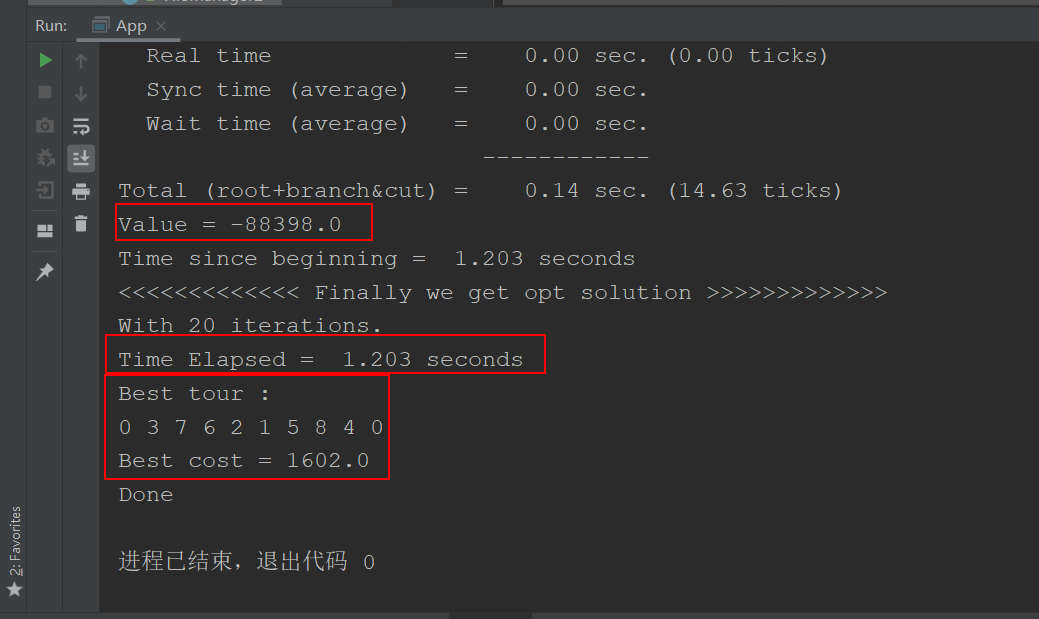
可以看到，对于测试算例（9个节点的小算例），两种方法得到的路径是一模一样的。下图中可以看到，新模型的目标值是-88398.0，正好等于9*(-10000)+1602.0 （M=10000），这与我们之前的推理也吻合。由于转化后问题的节点规模为原来的两倍，相应的算法时间消耗也扩大了很多（0.183s到1.203s）。

先提醒一下，如果问题存在不止一个最优解，可能两次得到的路径会不一样哦，小伙伴们自己测试时遇到了可别骂小编弄错了。

结语

自此，非对称TSP问题转化为对称TSP问题的方法已经介绍完了。值得一提的是，原作者1983年的论文还提出了一种针对局部非对称TSP问题（也就是部分节点距离不对称，部分对称）的转化方法，不需要增大节点规模到2n。可惜的是，该方法后来被证明有误，新解的结果只能作为原问题最优解的下界，作者在1986年的论文中承认了自己的错误。看来学术研究即使暂时被承认，也一样要经受时间的考验啊！

小编在查阅文献也时发现，较新的关于非对称问题的研究更多是直接设计对应算法，很少关于非对称TSP问题转对称的研究。或许是因为本文提到的方法已经相当经典，比较难有改进了吧。

参考文献：

1. Jonker, R., & Volgenant, T. (1986). Transforming asymmetric into symmetric traveling salesman problems: erratum. Operations Research Letters, 5(4), 215-216.
2. Jonker, R., & Volgenant, T. (1983). Transforming asymmetric into symmetric traveling salesman problems. Operations Research Letters, 2(4), 161-163.

代码下载：

关注公众号【数据魔术师】，在公众号内输入【ATSP】
或访问github：https://github.com/zll-hust/ATSP
即可获得本文代码文献！

最后

以上就是健壮篮球为你收集整理的非对称TSP问题（asymmetric travelling salesman problem）与对称TSP问题的转换的全部内容，希望文章能够帮你解决非对称TSP问题（asymmetric travelling salesman problem）与对称TSP问题的转换所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。