
作者 | THOMAS TANAY、LEWIS D GRIFFIN
译者 | 张建军
编辑 | 姗姗
出品 | 人工智能头条(公众号ID:AI_Thinker)
【导读】许多研究已经证明深度神经网络容易受到对抗性样本现象(adversarial example phenomenon)的影响:到目前为止测试的所有模型都可以通过图像的微小扰动使其分类显著改变。为了解决这个问题研究人员也在不断探索新方法,L2 正则化也被引入作为一种新技术。本文中人工智能头条将从基本问题——线性分类问题开始给大家介绍解决对抗性样本现象的一些新视角。
前言
以下是由目前最先进的训练来识别名人的网络对某实例所生成的预测:
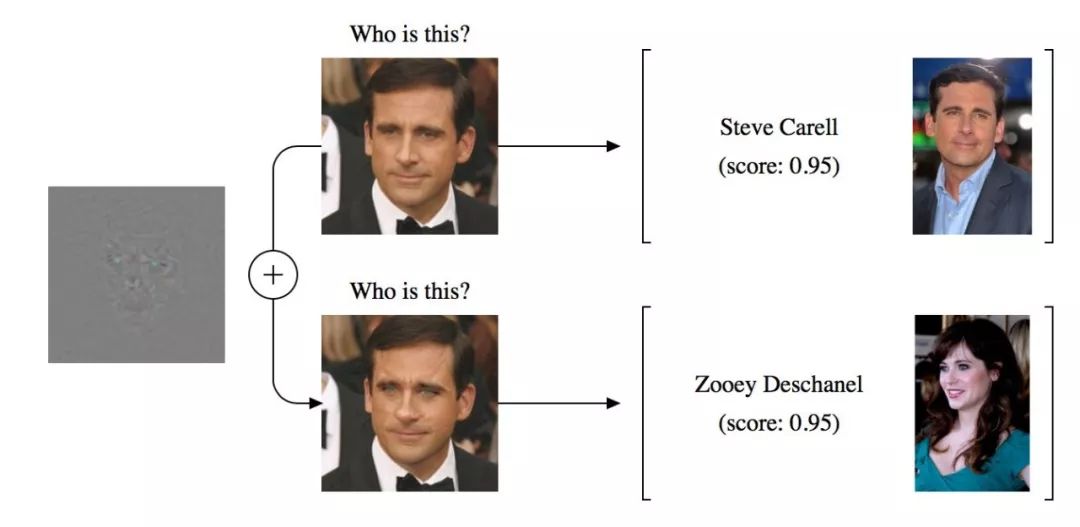
这个结果如此令人费解有两方面的原因。首先,它挑战了一个常见的想法,这个想法是,对新数据的良好泛化和对小扰动的鲁棒性应该是齐头并进的。其次,它对现实世界的应用构成了潜在的威胁。例如,麻省理工学院的研究人员最近已经成功构建了在相当多的角度和视角下都会被错误分类的 3D 物体。因此,理解这种现象并提高深度网络的鲁棒性已成为一个重要的研究目标。
针对这种现象,研究人员已经探索了几种方法。有些研究工作详细描述了这种现象并提供了一些理论分析。为了解决这个问题,人们尝试设计鲁棒性更强的网络结构或尝试在评估过程中检测对抗性样本。 对抗训练也被引入作为惩罚对抗方向的一种新的正则化技术。不幸的是,这个问题大部分都没有得到解决 。面对这个困难,我们建议从基本问题开始:首先关注线性分类,然后逐步增加问题复杂性。
玩具问题
在线性分类中,对抗性扰动通常被理解为高维度的点积的性质。一种普遍的直觉是:“对于高维问题,我们可以对输入进行许多无限小的改变,从而对输出进行一次大的改变” 。在这里,我们挑战这种直觉。我们认为,当分类边界靠近数据流形时,存在对抗性样本 – 并且其独立于图像空间维度。
▌设置
让我们从一个最小的玩具问题开始:一个二维图像空间,其中每个图像是 a 和 b 的函数。
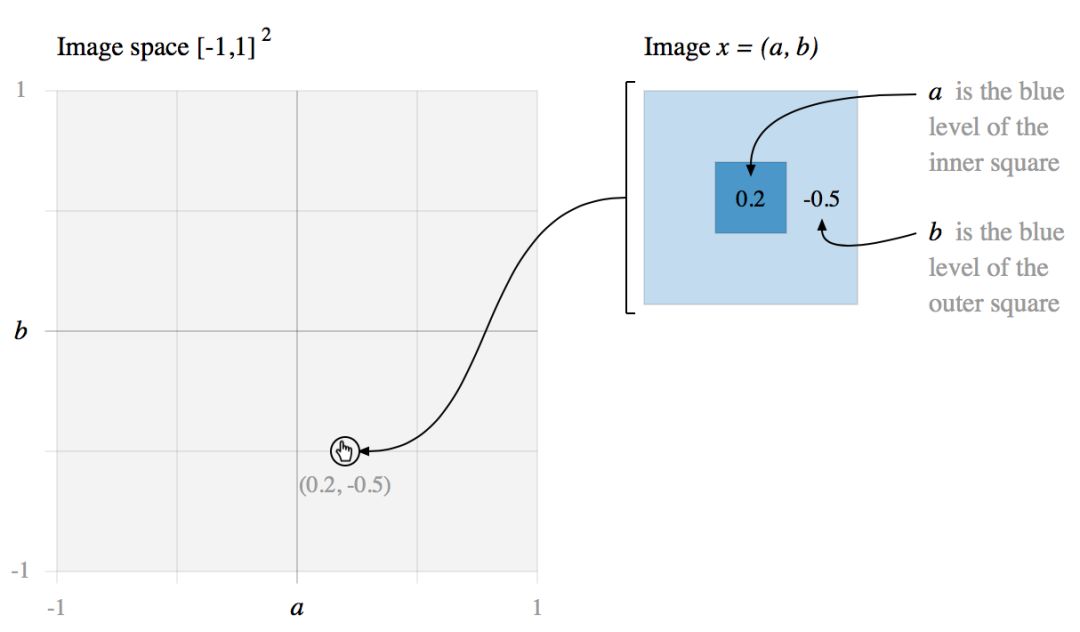
在这个简单的图像空间中,我们定义了两类图像
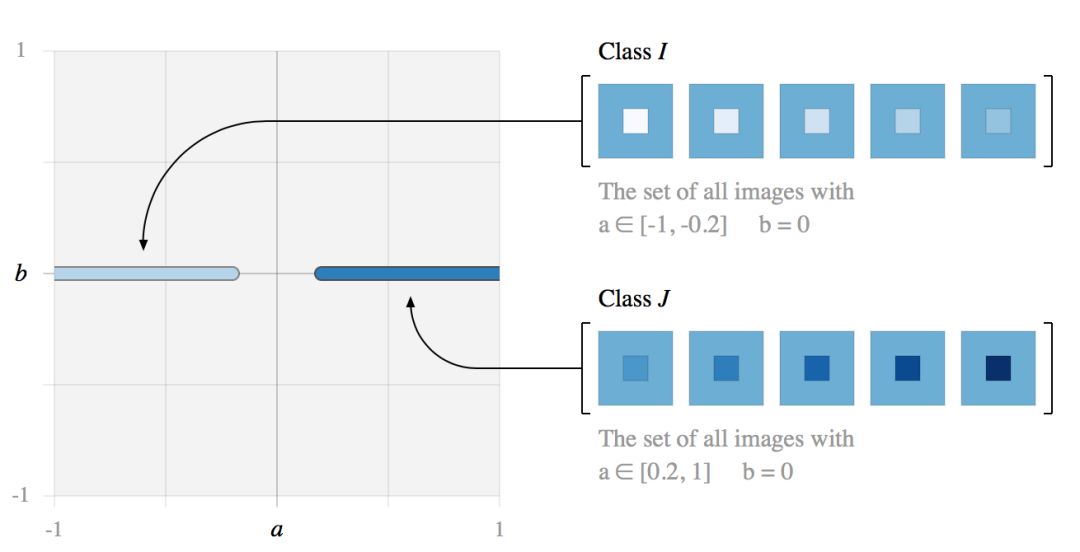
这两类图像可以用无数个线性分类器分开。例如考虑直线 Lθ。
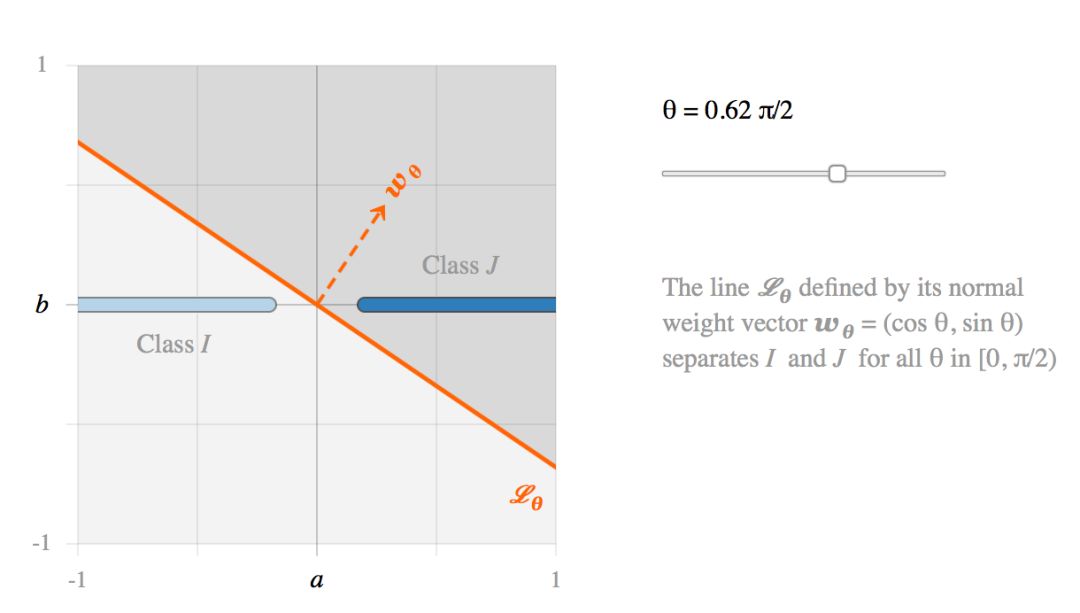
这就提出了第一个问题:如果所有的线性分类器 Lθ 都能很好地分离 I 和 J,那么他们是否对图像扰动具有相同的鲁棒性呢?
▌投影和镜像图像
考虑类 I 中的图像![]() 。距离x最近且属于相反类别的图像称为
。距离x最近且属于相反类别的图像称为 ![]() 在 Lθ 上投影图像(projected image):
在 Lθ 上投影图像(projected image):
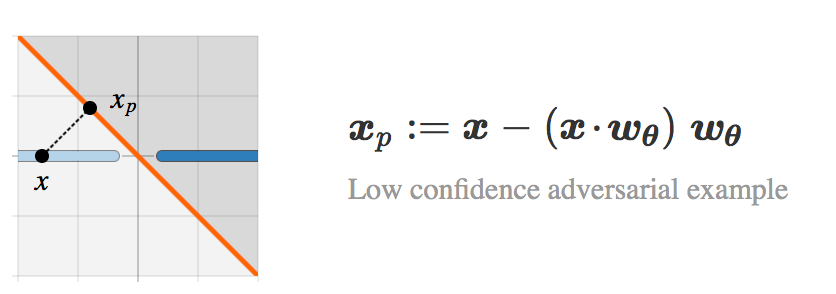
当 ![]() 和
和 ![]() 互相非常靠近时,我们说
互相非常靠近时,我们说 ![]() 是
是 ![]() 的一个对抗样本。请注意,
的一个对抗样本。请注意,![]() 的分类置信度比较低(它在分类边界上),我们考虑高分类置信度的对抗样本可能会更有趣。
的分类置信度比较低(它在分类边界上),我们考虑高分类置信度的对抗样本可能会更有趣。
下面,让我们来看看通过 Lθ 生成 ![]() 的镜像图像(mirror image)。
的镜像图像(mirror image)。
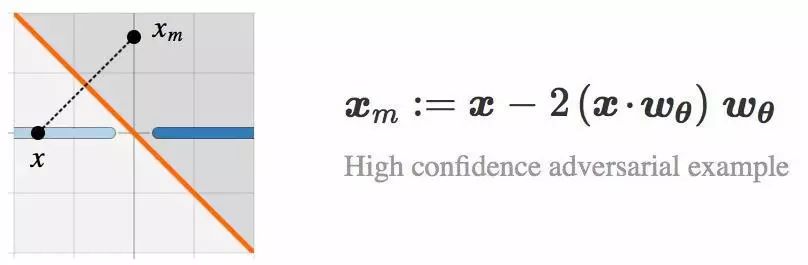
通过构造,![]() 和
和 ![]() 到分类边界的距离相同,而且具有相同的分类置信水平。
到分类边界的距离相同,而且具有相同的分类置信水平。
▌镜像图像作为θ的函数
回到我们的玩具问题上面来。我们现在可以把图像 ![]() 和它对应的镜像图像
和它对应的镜像图像 ![]() 作为 θ 的函数画出来。
作为 θ 的函数画出来。
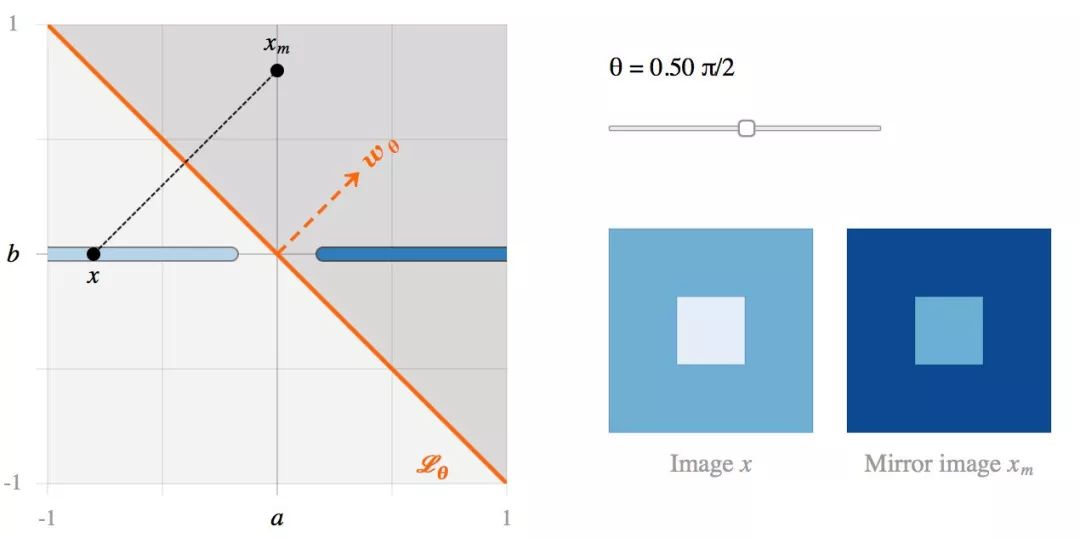
可以看到,![]() 和
和 ![]() 之间的距离依赖于角度 θ。有两种边界情形非常值得我们关注。
之间的距离依赖于角度 θ。有两种边界情形非常值得我们关注。
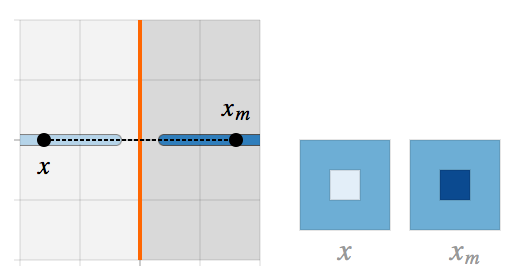
当θ = 0;Lθ 没有遇到对抗性样本的问题。![]() 以高置信度被分类为 I,而
以高置信度被分类为 I,而![]() 以高置信度被分类为 J,这与人类的观测符合。
以高置信度被分类为 J,这与人类的观测符合。
当θ -> π / 2;Lθ 遇到强对抗性样本的问题。![]() 以高置信度被分类为 I,而
以高置信度被分类为 I,而![]() 以高置信度被分类为 J,但是从视觉上很难把
以高置信度被分类为 J,但是从视觉上很难把 ![]() 和
和 ![]() 进行区分。
进行区分。
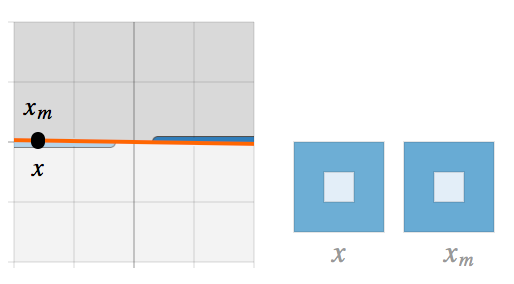
而这就提出了第二个问题:如果对抗性样本存在并且 Lθ 强烈倾斜,那么实际上是什么导致了 Lθ 倾斜的呢?
▌过拟合和L2正则化
我们的一个合理假设是,由标准线性学习算法(例如支持向量机(SVM)或逻辑回归)所定义的分类边界过拟合了训练集中的噪声数据点而导致了倾斜。有研究将鲁棒性与 SVM 中的正则化关联起来。这一假设也可以通过实验进行测试:旨在减少过拟合(如 L2 正则化)的技术有望减轻对抗性样本现象。
例如,我们考虑一个训练集,其中包含有一个噪声数据点 p。
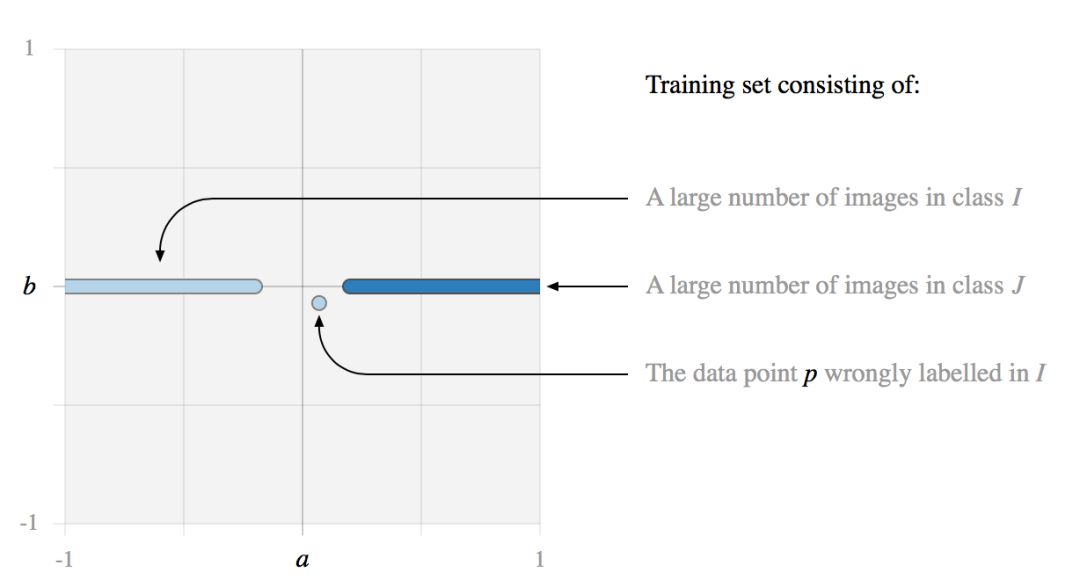
如果我们在这个训练数据集上训练一个 SVM 或者逻辑回归模型,我们会看到两种可能的行为。
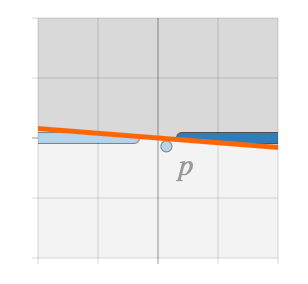
没有 L2 正则化:分类边界被强烈地倾斜。要完全拟合训练数据导致分类边界的倾斜角度过大。这个例子中,数据点 p 可以被正确地分类,但是训练得到的分类器非常容易受到对抗性样本的攻击。
有 L2 正则化:分类边界没有被倾斜。L2 正则化允许错误分类某些训练样本,从而减少了过拟合。当使用了足够的正则化,数据点 p 会被忽略,训练得到的分类器对对抗性样本具有强鲁棒性。
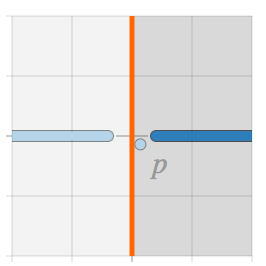
来到这里,一个合理的问题是——位于二维图像空间中的一维数据流形与高维的自然图像有什么关系?
线性分类中的对抗性样本
在下文中,我们可以表明在先前的玩具问题中介绍的两个主要思想在一般情况下保持有效:当分类边界靠近数据流形时存在对抗性样本,并且 L2 正则化可以控制分类边界的倾斜角度。
▌缩放损失函数
让我们从一个简单的观察现象开始:在训练期间,权重向量的范数表现为损失函数中的缩放参数。
▌设置
让 I 和 J 是两类图像,C 是超平面分类边界,它是定义在 ![]() 的一个线性分类器。C 由一个权重向量 w 和偏置 b 所指定。对于一张在
的一个线性分类器。C 由一个权重向量 w 和偏置 b 所指定。对于一张在 ![]() 上的图像
上的图像 ![]() ,我们把下面这个值叫做 C 对
,我们把下面这个值叫做 C 对 ![]() 的原始评分(raw score):
的原始评分(raw score):
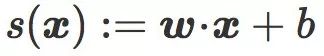
原始评分可以看作是 ![]() 和由 C 所定义的分类边界之间的有符号距离(signed distance)。特别地
和由 C 所定义的分类边界之间的有符号距离(signed distance)。特别地 ![]() 被分类为:
被分类为:
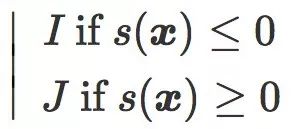
现在,我们考虑有一个含有 n 对(x, y)的训练集T,其中 ![]() 是图像
是图像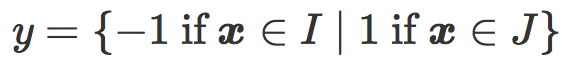 对应的标签。我们想知道在训练集 T 中下面这些量的分布:
对应的标签。我们想知道在训练集 T 中下面这些量的分布:
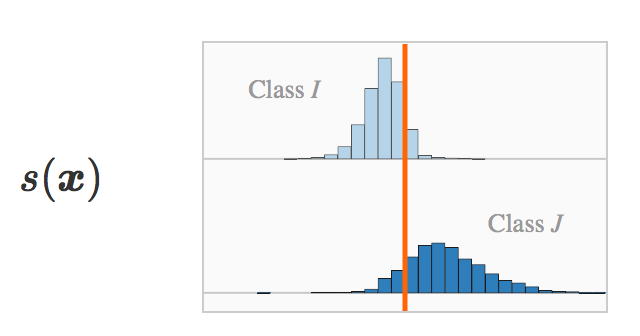
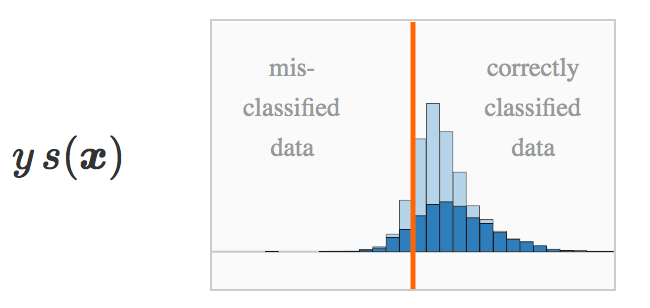
s(x) :如果我们画出由训练集得到的原始评分的直方图,那么我们可以得到两个有相反符号的堆。
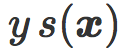 把 s(x) 和标签 y 相乘可以让我们把错误分类样本和正确分类样本分开。
把 s(x) 和标签 y 相乘可以让我们把错误分类样本和正确分类样本分开。
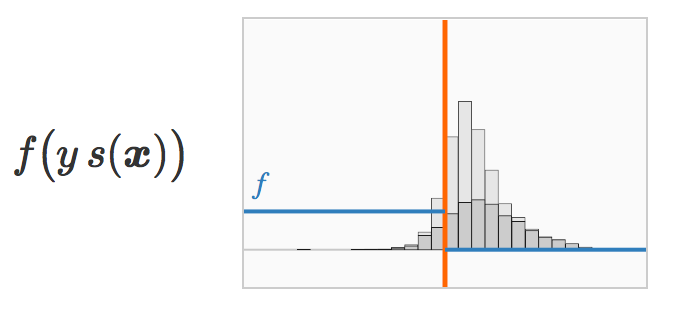
f(![]() ) 然后把损失函数作用在
) 然后把损失函数作用在 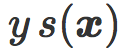 上我们可以对每个训练样本点 x 赋予一个惩罚值。
上我们可以对每个训练样本点 x 赋予一个惩罚值。
这时可以引入分类器 C 的经验风险的符号 R(w,b),其定义为在训练集 T 的平均惩罚值:
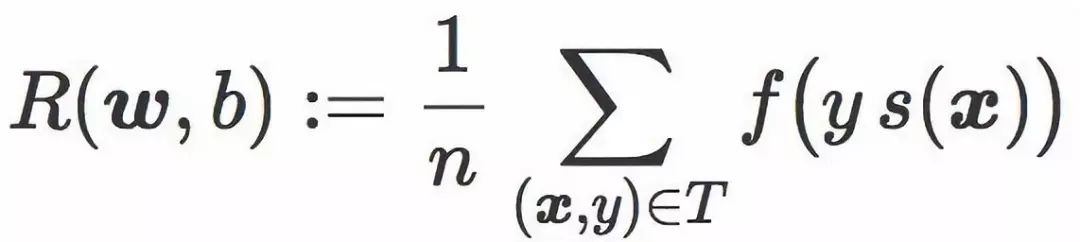
通常情况下,学习一个线性分类器其实就是针对一个选好的损失函数 f,寻找使 R(w,b) 最小化的权重向量 w 和偏置 b。
在二类分类中,三个值得注意的损失函数是:0-1 示函数、Hinge loss 、softplus loss。
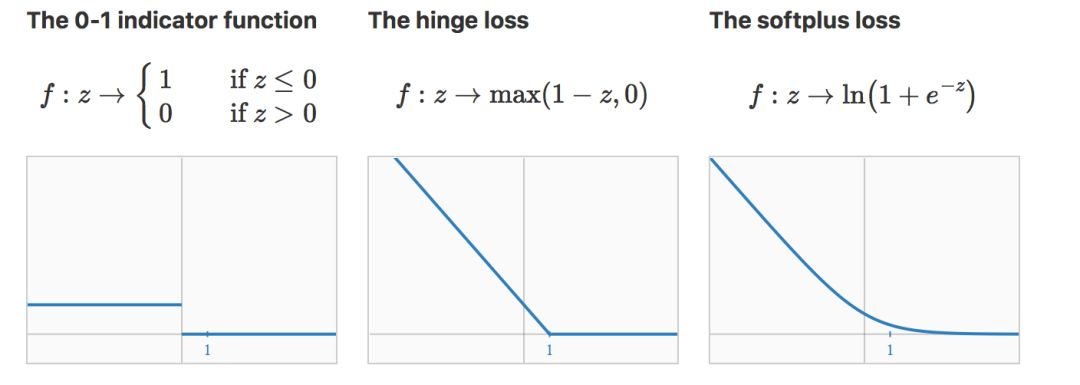
使用 0-1指示函数的话,经验风险就只是在 T 上的错误率(error rate)。某种程度来说,这个其实是最优的损失函数,因为实际问题中往往最小化误差率是我们追求的目标。
不幸的是,它和梯度下降不兼容(没有梯度可以下降:导数处处为 0(0 处不可导吧))。
这个缺点被 hinge loss(用在 SVM)和 softplus loss(用在逻辑回归)克服了,它们把 0-1 指示函数中的对错分数据的单位惩罚项替换为严格递减的惩罚项。请注意,hinge loss 和 softplus loss 都会对某些在分类边界附近的正确分类样本进行惩罚,这样可以有效保证安全间隔( safety margin)。
▌缩放参数 ![]()
之前忽视了一个重要的点,那就是有符号距离 s(x) 是被权重向量的范数所缩放的。如果 d(x) 是 x 和 C 之间的真实有符号欧氏距离(signed Euclidean distance),我们有:
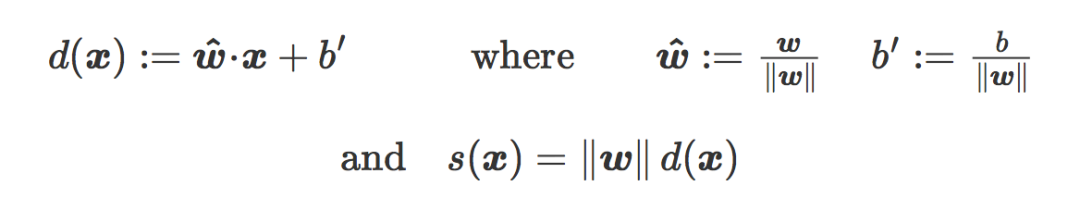
因此,范数 ![]() 可以被解读为在经验风险的表达式中损失函数的缩放参数:
可以被解读为在经验风险的表达式中损失函数的缩放参数:
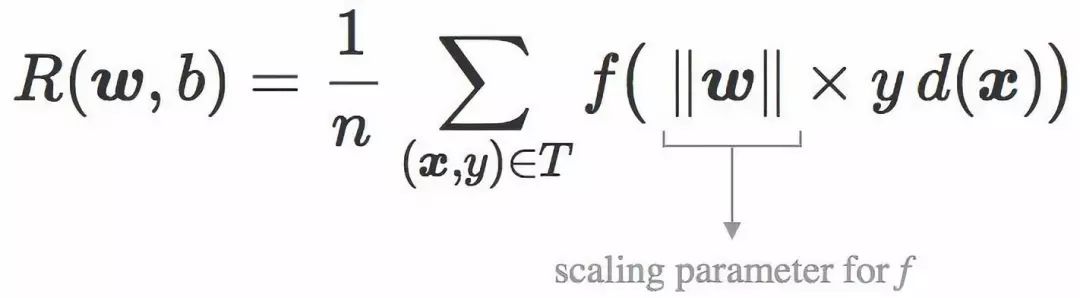
让我们定义缩放损失函数 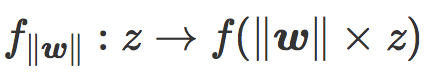 。
。
我们观察到 0-1指示函数对缩放具有不变性,而 hinge loss 和 softplus loss则会受缩放的强烈影响。
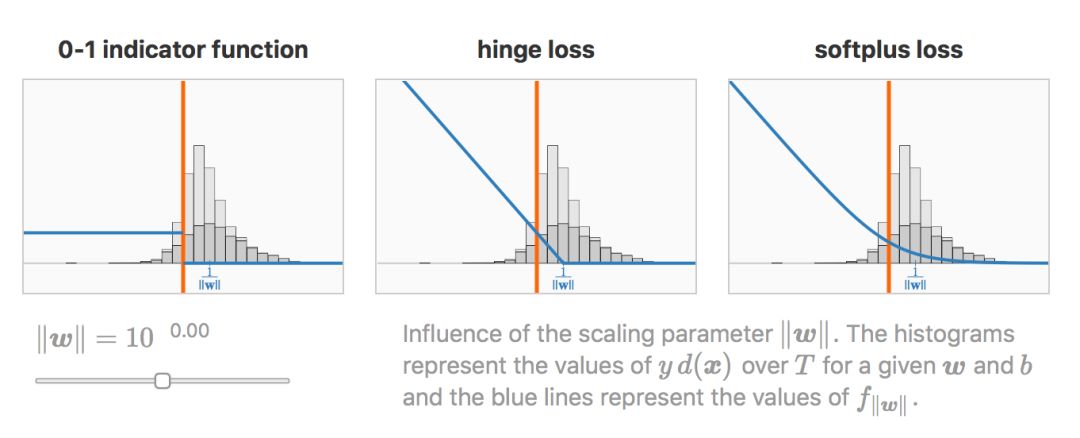
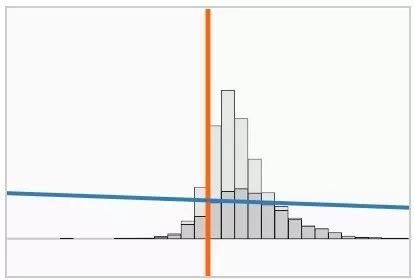
缩放参数 ![]() 的影响:直方图表示对于一个给定 w 和 b,
的影响:直方图表示对于一个给定 w 和 b,![]() 在T上的值,蓝线则表示
在T上的值,蓝线则表示 ![]() 的值。
的值。
明显地,对于缩放参数的极端值,hinge loss 和 softplus loss行为一致。
当 ![]() 很大时,Hinge loss 和 softplus loss 只惩罚错分样本,而且是以线性的方式。
很大时,Hinge loss 和 softplus loss 只惩罚错分样本,而且是以线性的方式。
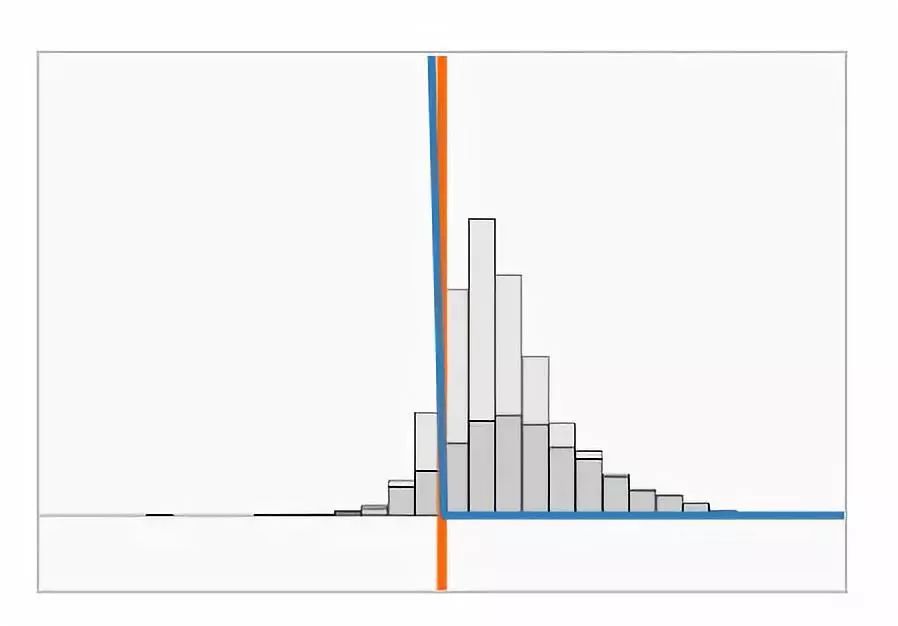
更精确地,两个损失函数都满足:
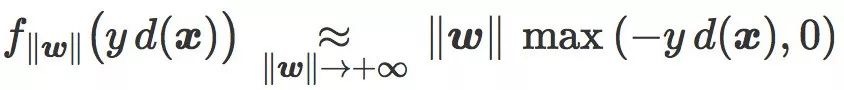
为了简便,我们把错分数据的集合定义为:
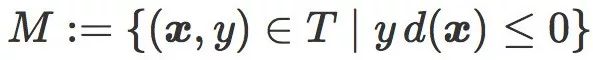
然后我们可以把经验风险写成:
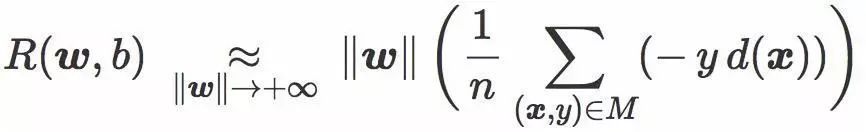
这个表达式包含一个我们称为误差距离(error distance)的项:
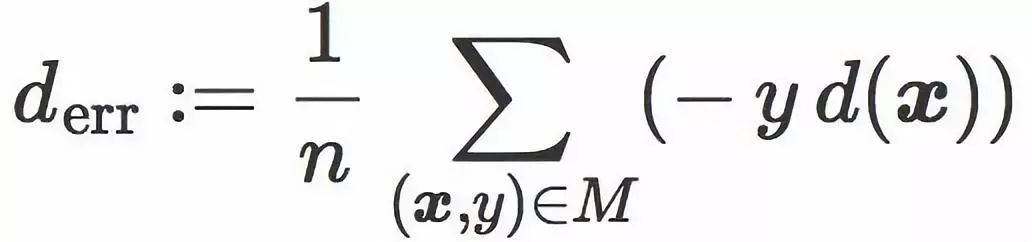
这项为正数,而且可以被解读为每个训练样本被 C 错分的平均距离(正确分类样本对这项贡献为 0)。它和训练误差相关 — 虽然并不完全等价。
最后,我们有:
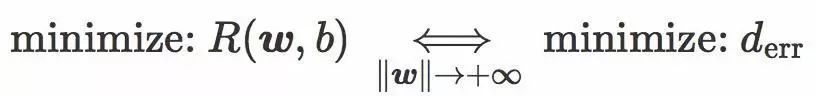
用文字来描述就是:
当 ![]() 很大时,针对 hinge loss 或者 softplus loss 最小化经验风险等价于最小化误差距离,这和最小化训练数据集的误差率相似。
很大时,针对 hinge loss 或者 softplus loss 最小化经验风险等价于最小化误差距离,这和最小化训练数据集的误差率相似。
当 ![]() 很小时,Hinge loss 和 softplus loss 线性惩罚整个训练数据集。
很小时,Hinge loss 和 softplus loss 线性惩罚整个训练数据集。
更精确地,两个损失函数都满足:α 和 β 是两个正数。
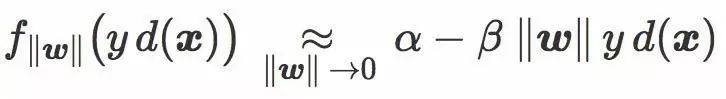
然后我们可以把经验风险写成:
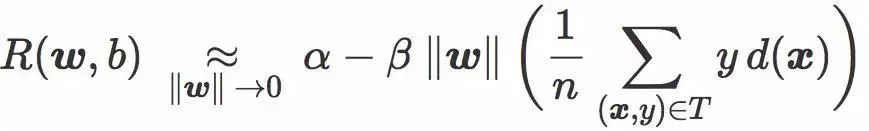
该表达式包含了一个我们称为对抗距离(adversarial distance)的项:
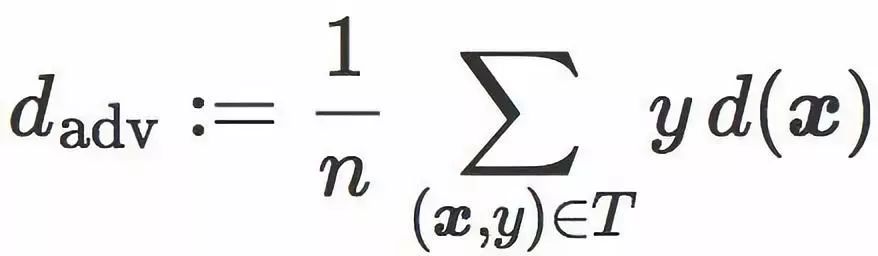
该项是 T 中的图像和分类边界 C 之间的平均距离(错分图像对该项的贡献为
负)。它可以看作是针对对抗性扰动的鲁棒性度量:当 ![]() 很大时,错分图像的数量很少而且正确分类图像距离 C 很远。
很大时,错分图像的数量很少而且正确分类图像距离 C 很远。
最后,我们有:
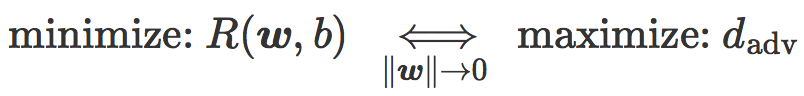
用文字来描述就是,当 ![]() 很小时,针对 hinge loss 或者 softplus loss 最小化经验风险等价于最大化对抗距离,这可以解读为最小化对抗性样本现象。
很小时,针对 hinge loss 或者 softplus loss 最小化经验风险等价于最大化对抗距离,这可以解读为最小化对抗性样本现象。
▌结束语
实践中,![]() 的值可以通过往经验风险中添加一个正则项来进行控制,这引出了正则化损失函数:小的正则化参数λ允许不受限制地变大,而大的 λ 则鼓励变小。
的值可以通过往经验风险中添加一个正则项来进行控制,这引出了正则化损失函数:小的正则化参数λ允许不受限制地变大,而大的 λ 则鼓励变小。

总的来说,线性分类中的两个标准模型(SVM 和逻辑回归)平衡了两个目标:当正则项小时他们最小化误差距离,而当正则项大时他们最大化对抗距离。
对抗距离和倾斜角度
上一节中出现了对抗距离,其可以作为针对对抗性扰动的鲁棒性度量。相当方便地,它可以表示为单个参数的函数:该参数为分类边界和最近质心分类器之间的角度。
假设 ![]() 和
和 ![]() 分别是 T 在 I 和 J 的元素集合,我们可以写成:
分别是 T 在 I 和 J 的元素集合,我们可以写成:
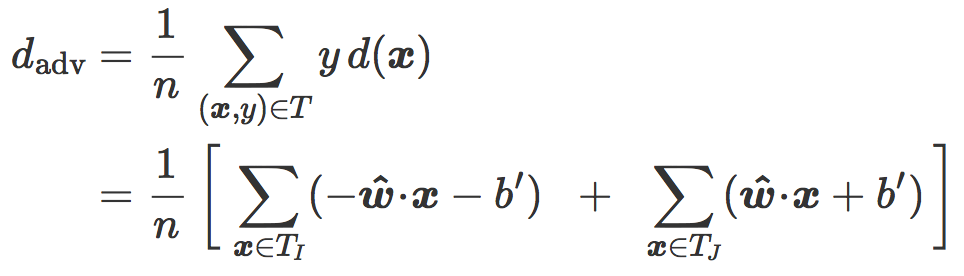
如果 ![]() 和
和 ![]() 数量平衡
数量平衡 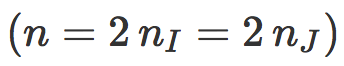 :
:
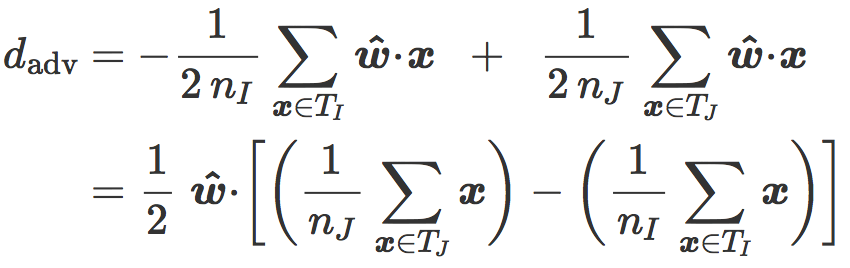
假设 i 和 j 分别是 ![]() 和
和 ![]() 的质心:
的质心:
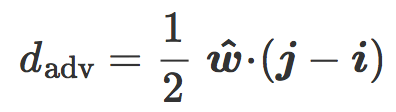
我们现在介绍最近质心分类器(Nearest centroid classifier),它的法向量是 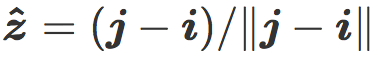 ,从而:
,从而:
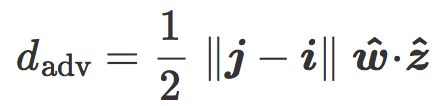
最后我们把含有 ![]() 和
和 ![]() 的平面叫做 C 的倾斜平面,把
的平面叫做 C 的倾斜平面,把 ![]() 和
和 ![]() 之间的角度 θ 叫做 C 的倾斜角度:
之间的角度 θ 叫做 C 的倾斜角度:
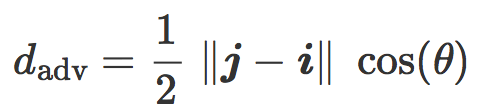
该公式可以在倾斜平面中用几何表示:是分类边界 C 与两个质心 i 和 j 之间的平均距离。
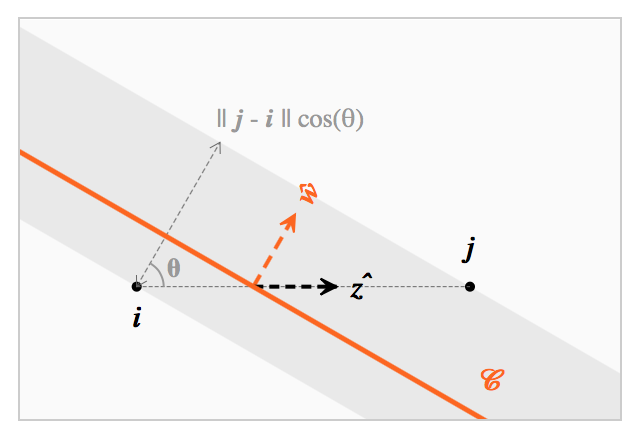
在一个给定的、两质心距离 ![]() 固定的训练数据集T上,
固定的训练数据集T上,![]() 只依赖于倾斜角度 θ。这里有两个发现:
只依赖于倾斜角度 θ。这里有两个发现:
-
对抗性样本现象被最近质心分类器最小化(θ=0)
-
当 θ -> π / 2 时,对抗性样本具有任意强度(正如玩具问题小节中的分类器 Lθ)。
示例:MNIST上的SVM
我们现在用 MNIST 数字的二分类问题作为例子来解释上面的发现。对每对可能的数字类别,我们训练多个 SVM 模型(w, b),正则化参数 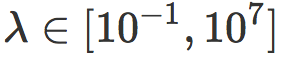 ,每个类别取 3000 张图片作为训练集。
,每个类别取 3000 张图片作为训练集。
我们把训练数据和分类边界之间距离 ![]() 的分布作为正则化参数 λ 的函数,并画出它的直方图(灰色直方图)。每个模型收敛后(蓝线),我们把缩放后的损失函数进行叠加。
的分布作为正则化参数 λ 的函数,并画出它的直方图(灰色直方图)。每个模型收敛后(蓝线),我们把缩放后的损失函数进行叠加。
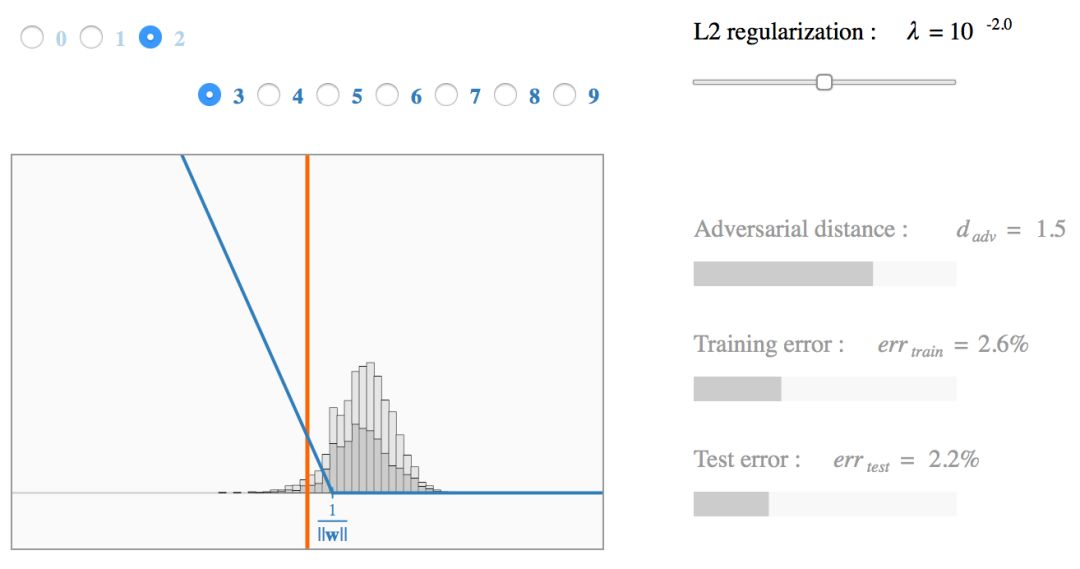
我们可以发现,hinge loss 的缩放对获得的模型有明显的影响。不幸的是,最小化训练误差和最大化对抗距离是矛盾的两个目标:当 λ 小时 ![]()
被最小化,而当 λ 大时 ![]() 被最大化。请注意,测试误差在某个中间水平的正则化参数
被最大化。请注意,测试误差在某个中间水平的正则化参数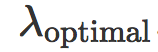 下被最小化。当
下被最小化。当 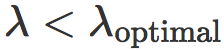 分类器过拟合,而当
分类器过拟合,而当 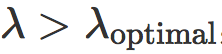 ,分类器欠拟合。
,分类器欠拟合。
为了更好地理解如何平衡这两个目标,我们可以用一个不同的角度来看看训练数据。
首先我们计算最近质心分类器的单位权重向量。然后对于每个 SVM 模型(w, b),我们计算单位向量 ![]() 使得
使得 ![]() 是 w 的倾斜平面的一个标准正交基。最后,我们把训练数据投影到
是 w 的倾斜平面的一个标准正交基。最后,我们把训练数据投影到 ![]() 。
。
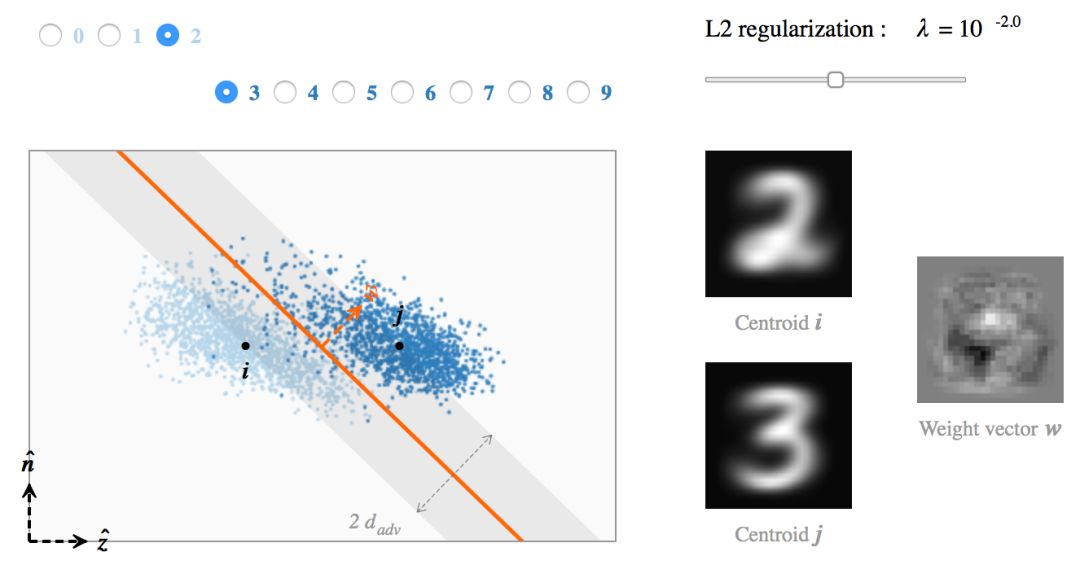
水平方向经过两个质心,竖直方向的选择则是使得 w 属于该平面(超平面边界表现为一条直线)。请注意,因为 ![]() 是一个标准正交基,所以在该平面上的距离是真实的像素距离。想要理解为什么当λ变化时数据点好像在四处移动,我们需要想象一下倾斜平面在 784 维的输入空间中围绕着
是一个标准正交基,所以在该平面上的距离是真实的像素距离。想要理解为什么当λ变化时数据点好像在四处移动,我们需要想象一下倾斜平面在 784 维的输入空间中围绕着 ![]() 在旋转(因此对于每个 λ 的值,展示的是 784 维训练数据的不同部分)。
在旋转(因此对于每个 λ 的值,展示的是 784 维训练数据的不同部分)。
对于高正则化水平,模型与最近质心分类器平行且对抗距离被最大化。当 λ 变小时,分类边界往低方差的方向倾斜从而提高对训练数据的拟合程度。最终,一小部分的错分样本被过拟合,导致对抗距离很小,而且很难解读权重向量。
最后,我们可以看看每个模型中的两个代表性样本 x, y(每类一个)以及他们的镜像图像 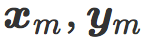 。他们在 w 的倾斜平面上的投影可以直观反映线性分类中的对抗性样本现象。
。他们在 w 的倾斜平面上的投影可以直观反映线性分类中的对抗性样本现象。
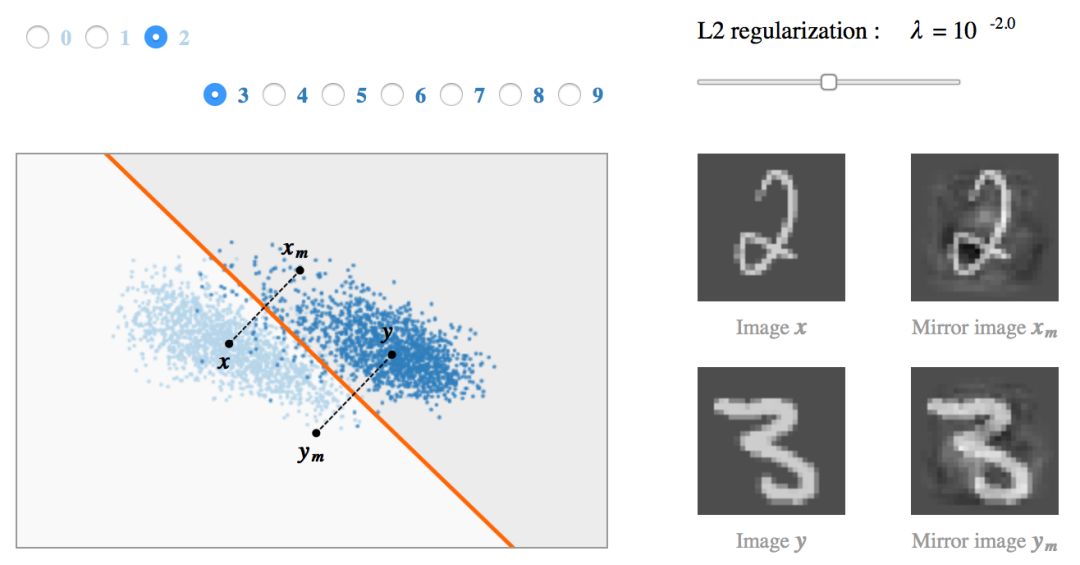
当倾斜角度趋近 π / 2 时,模型对强对抗性样本很敏感 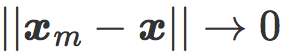 且
且 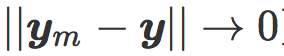 。这是强过拟合的症状,而过拟合是否出现取决于把两类分开的困难程度(例如,比较一下 7 和 9 的分类,以及 0 和 1 的分类)
。这是强过拟合的症状,而过拟合是否出现取决于把两类分开的困难程度(例如,比较一下 7 和 9 的分类,以及 0 和 1 的分类)
神经网络中的对抗性样本
多亏了对抗距离和倾斜角度之间的等价性,线性情况才能很简单地在平面中进行可视化。然而在神经网络中,分类边界并不平整且对抗距离并不能缩减到单一一个参数。尽管如此,两者依然有相似之处。
▌第一步:两层二分类网络
让 ![]() 是一个有一个输出单元两层网络,其定义了在
是一个有一个输出单元两层网络,其定义了在![]() 上的一个非线性二类分类器。
上的一个非线性二类分类器。![]() 的第一层由一个权重矩阵 W1和一个偏置向量 b1 指定,第二层由一个权重矩阵 W2 和一个偏置向量 b2 指定。我们假设这两层被一个层
的第一层由一个权重矩阵 W1和一个偏置向量 b1 指定,第二层由一个权重矩阵 W2 和一个偏置向量 b2 指定。我们假设这两层被一个层 ![]() 所分开,
所分开,![]() 包含有整流线性单元,对每个输入执行函数
包含有整流线性单元,对每个输入执行函数 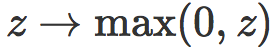 。对于一张在
。对于一张在 ![]() 的图像 x,我们把下面这个值叫做
的图像 x,我们把下面这个值叫做 ![]() 对 x 的原始评分:
对 x 的原始评分:
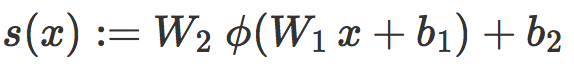
和线性情况类似,针对一个损失函数 f 在 T 上的经验风险可以写成:
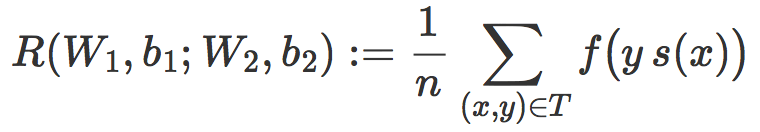
而训练 ![]() 其实就是针对一个选好的 f 找到使得 R 最小化的 W1,b1, W2 和b2。
其实就是针对一个选好的 f 找到使得 R 最小化的 W1,b1, W2 和b2。
![]() 是分段线性函数,且在每张图像 x 附近存在一个局部线性区域
是分段线性函数,且在每张图像 x 附近存在一个局部线性区域 ![]() ,在这区域中:
,在这区域中:
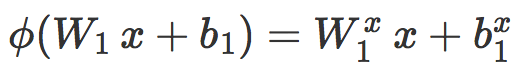
其中 ![]() 和
和 ![]() 是分别对 W1 和 b1 的某些直线取 0 得到的。在
是分别对 W1 和 b1 的某些直线取 0 得到的。在 ![]() 中,原始评分可以写成:
中,原始评分可以写成:
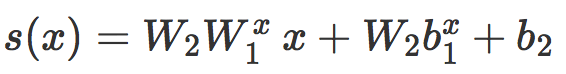
这可以看作是一个局部线性分类器 Cx 的原始评分,而且我们对线性情况的分析可以几乎不需修改就可以应用到这里。首先,我们发现 s(x) 是一个缩放距离。如果 d(x) 是 x 和 Cx 之间的真实有符号欧氏距离,那么我们有:
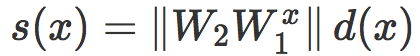
注意:
-
d(x) 可以看做是 x 和由 N 定义的分类边界之间距离的线性近似(到最近对抗性样本的距离)
-
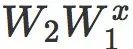 是 N 在
是 N 在 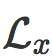 中的梯度。它是 x 的对抗方向,实践中可以由反向传播进行计算。
中的梯度。它是 x 的对抗方向,实践中可以由反向传播进行计算。
范数 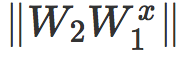 可以被解读为损失函数的一个缩放参数(现在缩放是局部的,依赖于 x)。同时控制所有的局部缩放的一个简单方法是,往独立作用于范数
可以被解读为损失函数的一个缩放参数(现在缩放是局部的,依赖于 x)。同时控制所有的局部缩放的一个简单方法是,往独立作用于范数
![]() 和
和 ![]() 的经验风险添加一个 L2 正则项(不要忘了 W1 中的权重
的经验风险添加一个 L2 正则项(不要忘了 W1 中的权重 ![]() 是的权重的一个子集)。通过梯度下降,这和在每次迭代中衰减权重 W1 和 W2 等价。更精确地,对于一个学习率 η 和一个衰减因子 λ,权重衰减更新定义为:
是的权重的一个子集)。通过梯度下降,这和在每次迭代中衰减权重 W1 和 W2 等价。更精确地,对于一个学习率 η 和一个衰减因子 λ,权重衰减更新定义为:
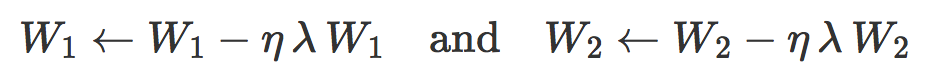
-
当衰减因子 λ 很小时,缩放参数
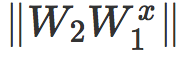 允许不受限制地增长且损失函数只惩罚错分样本。最小化经验风险等价于最小化训练数据集上的误差。
允许不受限制地增长且损失函数只惩罚错分样本。最小化经验风险等价于最小化训练数据集上的误差。 -
随着衰减因子变大,缩放参数
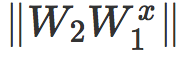 减小且损失函数开始惩罚越来越多的正确分类样本,将其往远离边界的方向推开。这种情况下,L2 权重衰减可以看成是对抗性训练的一种形式。
减小且损失函数开始惩罚越来越多的正确分类样本,将其往远离边界的方向推开。这种情况下,L2 权重衰减可以看成是对抗性训练的一种形式。
总的来说,L2正则化在损失函数中起缩放的作用,无论是在线性分类中还是在小型神经网络中。通过梯度下降,高权重衰减可以看成是对抗性训练的一种简单形式。
▌第二步:一般情形
上面的分析可以推广到更多层,甚至推广到非分段线性激活函数。一个重要的发现是,我们总有:

其中 ![]() 是对 x 的原始评分的梯度,
是对 x 的原始评分的梯度,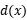 是 x 和由该网络所定义的分类边界之间距离的线性近似。范数
是 x 和由该网络所定义的分类边界之间距离的线性近似。范数![]() 则成为损失函数的一个缩放参数,该参数可以通过权重衰减来进行控制。
则成为损失函数的一个缩放参数,该参数可以通过权重衰减来进行控制。
这个想法还可以扩充到多分类的问题。在多分类情形中,原始评分变成一个向量,其中每个元素被叫做 logits。每个logits ![]() 通过应用 softmax 函数转化成一个概率
通过应用 softmax 函数转化成一个概率 ![]() :
:
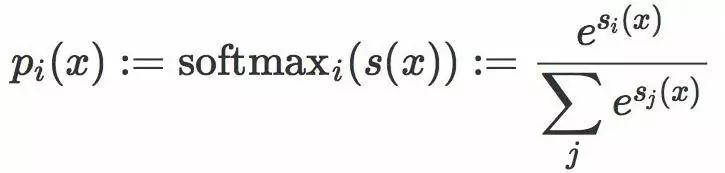
对于每个图像/标签对(x, y),和正确类别关联的概率是 ![]() 。通过对(x, y)添加以下惩罚项,对数似然损失函数(log-likelihood loss function)鼓励这个概率逼近1:
。通过对(x, y)添加以下惩罚项,对数似然损失函数(log-likelihood loss function)鼓励这个概率逼近1:
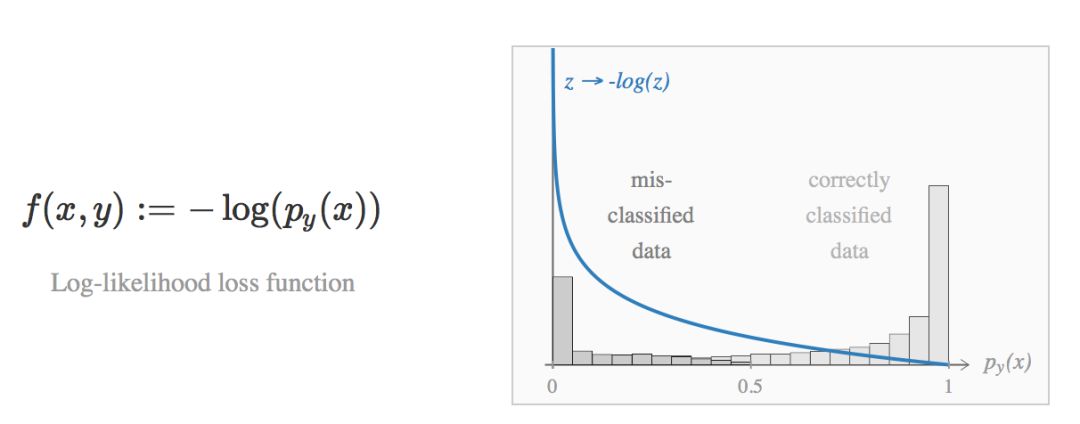
现在,改变权重衰减影响logits的缩放,实际上的作用正和 softmax 函数的温度参数(temperature parameter)一样。当权重衰减很低,生成的概率分布接近独热编码(one-hot encodings)(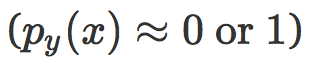 ),而且只有错分样本才会生成非 0 惩罚值。然而,当权重衰减很高时,生成的概率分布很平滑,正确分类的数据开始参与到训练当中来,从而避免了过拟合。
),而且只有错分样本才会生成非 0 惩罚值。然而,当权重衰减很高时,生成的概率分布很平滑,正确分类的数据开始参与到训练当中来,从而避免了过拟合。
在实践中,许多发现都表明现代的深度网络是低正则化(under-regularized)的:
-
它们的校正效果很差,而且经常生成过于自信的预测。
-
它们经常收敛到 0 训练误差,即使是在一组随机标记的数据上。
-
它们经常容易受到微小扰动的线性攻击从而效果变差。
示例:MNIST上的LeNet
是否有可能仅仅通过使用权重衰减来达到正则化一个神经网络的目的,从而使其可以对付对抗性样本呢?想法非常简单而且以前已经有人考虑过了:Goodfellow 等人发现对抗性训练在线性情况下“和 L1 正则化有几分相似”。然而,作者指出,当在 MNIST 训练 maxout 网络时,L1 权重衰减系数为0.0025 “太大了,导致模型在训练数据集上的误差一直高于 5%。更小的权重衰减系数可以更成功地训练,但是却失去了正则化的好处”。我们再次把这个想法付诸实践,而且我们的发现有更细微的差别。尽管使用高权重衰减显然不是万能药,我们发现它可以减少对抗性样本现象,只需简单设置一下即可。
考虑 MNIST(10分类问题)上的 LeNet。我们使用基线的 MatConvNet 实现,它的结构如下:

我们用一个低权重衰减 ![]() 训练网络作为其中一个版本,然后用一个高权重衰减
训练网络作为其中一个版本,然后用一个高权重衰减 ![]() 训练网络作为另外一个版本(我们用
训练网络作为另外一个版本(我们用 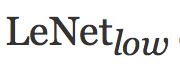 和
和  来分别指代这两个网络)。我们固定其它所有参数:训练 50 代,批次大小为 300,学习率为 0.0005,动量为 0.9。
来分别指代这两个网络)。我们固定其它所有参数:训练 50 代,批次大小为 300,学习率为 0.0005,动量为 0.9。
我们有以下几个发现。首先,让我们先把两个网络的训练和测试误差作为训练迭代次数的函数画在图上。
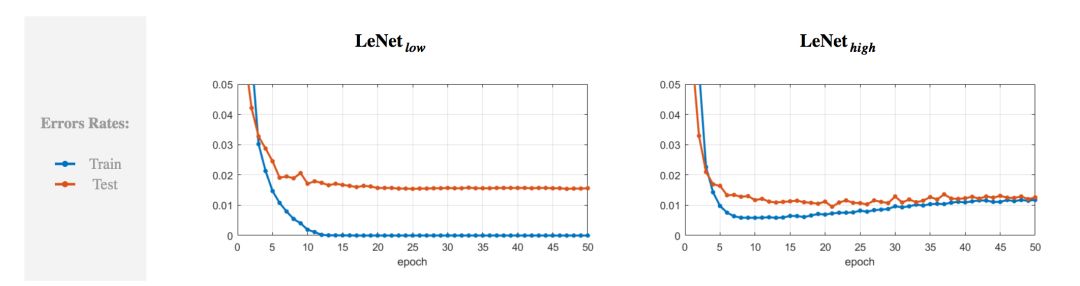
我们可以发现  过拟合程度较低(训练结束时训练和测试误差大约相等),效果比
过拟合程度较低(训练结束时训练和测试误差大约相等),效果比  稍好(最终测试误差为 1.2% vs 1.6%)。
稍好(最终测试误差为 1.2% vs 1.6%)。
和
我们还可以深入观察一下学习到的权重。下面,我们计算它们的均方根误差(RMS)并对每个卷积层展示随机选择的一个滤波器(filter)。
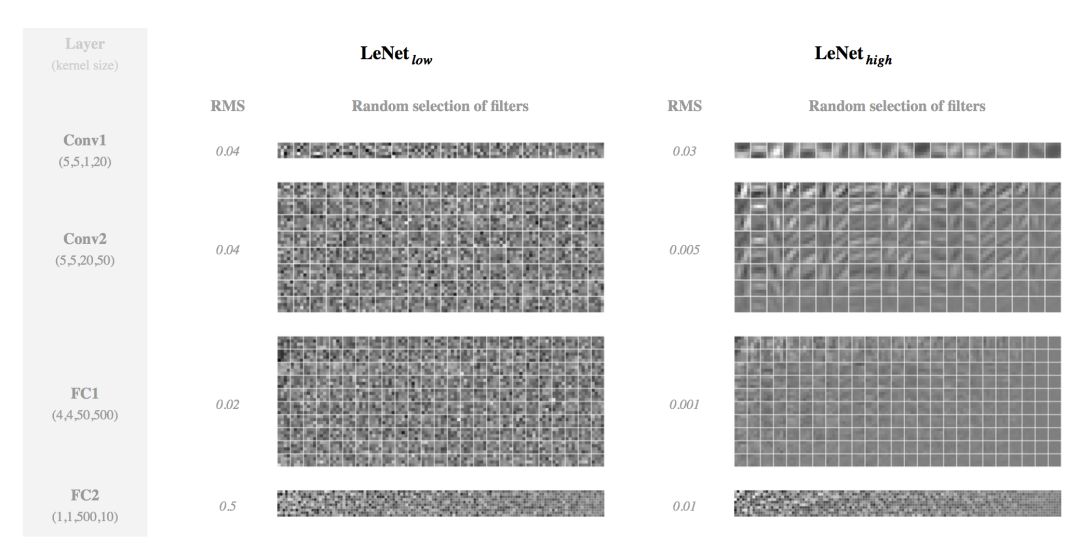
正和期望的一样,用高权重衰减学到的权重有更低的 RMS。 的滤波器比
的滤波器比  的更加平滑(看看 Conv1 和 Conv2 中出现的清晰边缘检测器),而且它们的大小在每个卷积层内的变化更大(看看 Conv2 和 FC1 中出现的均匀灰色滤波器)。
的更加平滑(看看 Conv1 和 Conv2 中出现的清晰边缘检测器),而且它们的大小在每个卷积层内的变化更大(看看 Conv2 和 FC1 中出现的均匀灰色滤波器)。
最后,让我们用这两个网络进行同样的视觉评估:对于每个数字的任何一个实例,我们生成一个高置信度的对抗性样本,并对标签进行循环置换,即 0->1, 1->2, …, 9->0。特别地,生成的每个对抗性样本是通过对希望得到的标签的概率执行梯度上升,直到中位数为 0.95 为止而得到的。我们在下面展示10 张原始图像 OI,两个网络对应的对抗性样本 AE,以及它们的对抗性扰动Pert。
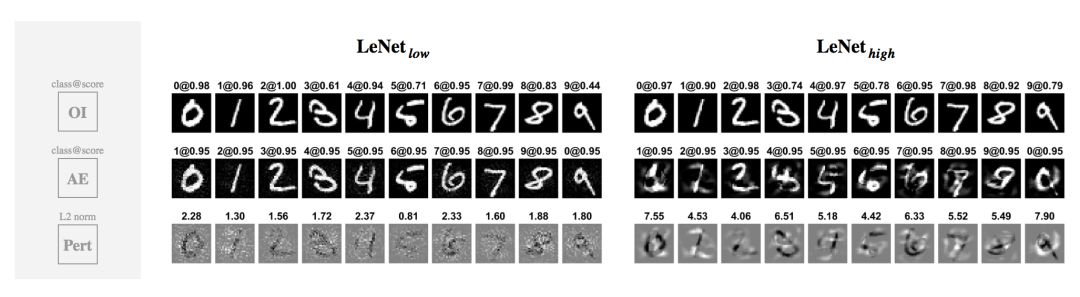
我们可以发现, 比
比 更不易受对抗性样本的影响;对抗性扰动有更高的 L2 范数,而且对于人类观察者来说更有意义。
更不易受对抗性样本的影响;对抗性扰动有更高的 L2 范数,而且对于人类观察者来说更有意义。
更进一步的想法
尽管多年来它吸引了广泛的关注,尽管在理论上和实践中它都对机器学习至关重要,对抗性样本现象目前依然有许多问题亟待解决。本文的主要目的是为线性情况下的对抗性样本现象提供一个清晰和直观的印象,希望为继续往这个方向前行建立一个坚定的基石。非常偶然地,我们发现,L2 权重衰减在MNIST 上的小型神经网络中扮演着比以前更加重要的角色。
然而,当网络变深,数据集变复杂之后,情况就不一样了。根据我们的经验,模型非线性程度越高,权重衰减在解决这个问题上就越无能为力。这个局限可能只是表面现象,或许值得我们在这里再稍微深入介绍一下本文的发现(例如,我们应该更加关注在训练时对 logits 的缩放)。又或者深度网络的高度非线性可能对L2正则化实现的初阶对抗性训练造成障碍。我们认为,要真正令人满意地解决这个问题,急需要在深度学习方面的深刻的全新想法。
更多参考内容可访问原文链接:
https://thomas-tanay.github.io/post--L2-regularization
*本文由人工智能头条整理编译,转载请联系编辑(微信1092722531)
最后
以上就是神勇奇迹最近收集整理的关于敲重点!一文详解解决对抗性样本问题的新方法——L2正则化法的全部内容,更多相关敲重点!一文详解解决对抗性样本问题内容请搜索靠谱客的其他文章。








发表评论 取消回复