本文讲的是手动生成数据，可视化生成的数据，以及可视化模型训练之后的数据。附有代码和解释。
-
- 生成点数据和绘制散点图
- 可视化绘制机器学习模型预测之后的结果
- 对npmeshgrid方法的解释
- 附录
先上效果图：
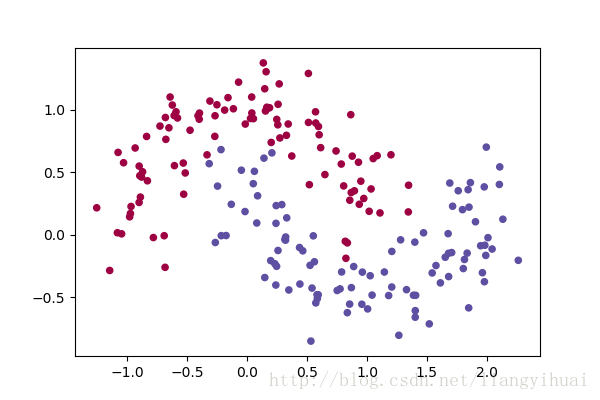
图一：绘制双月亮型的散点图
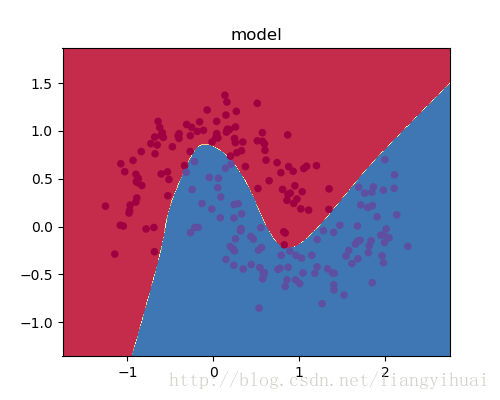
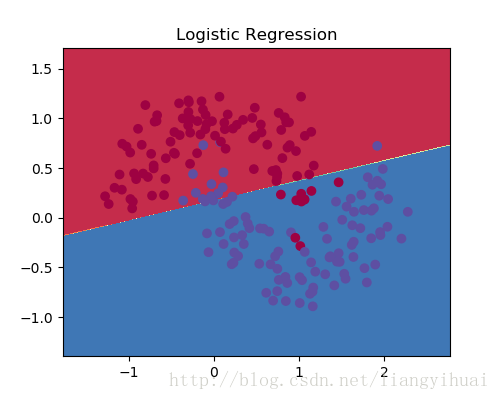
图2-2：显示线性模型的逻辑回归分类的结果
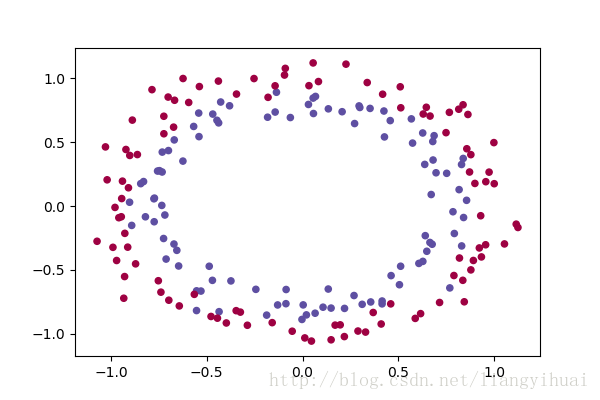
图二：绘制双圆形散点图。
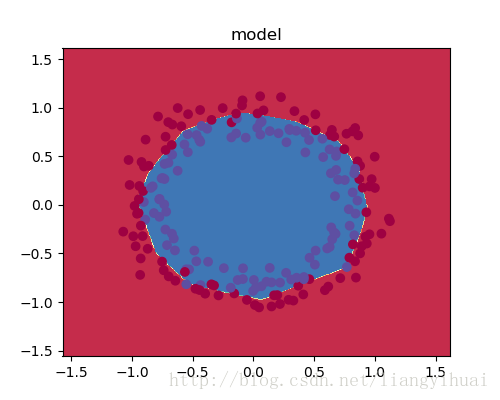
图2-2： 可视化分类结果
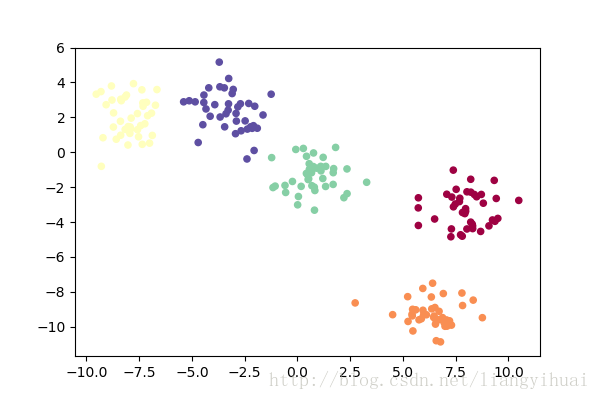
图三：绘制多聚类散点图
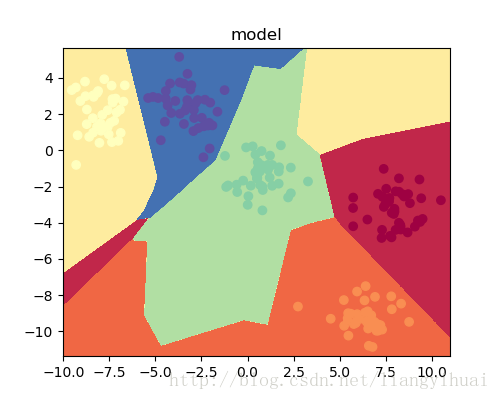
图3-3：可视化分类结果
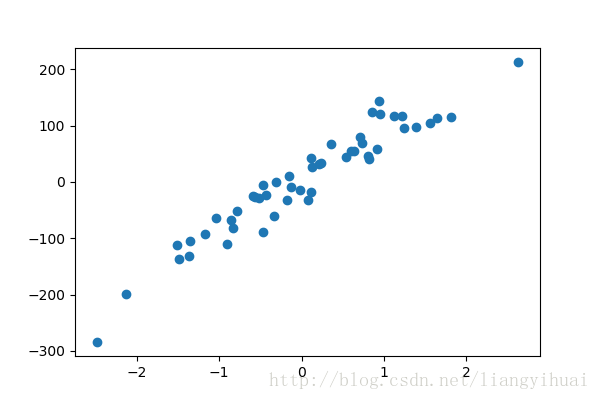
图四：绘制回归散点图
生成点数据和绘制散点图
使用python的sklearn和matplotlib可以生成点数据以及绘制和显示它们。上图所示的点都是二维的，也就是x和y轴。对于多维的数据也是可以生成的，但是，多维的数据不容易绘制和展示，特别是超过三维之后。
对于图一的双月亮型的散点图，x的shape是（n, 2），y是一个数组。如果要把这些数据绘制成第一张图所示的样子，需要把X的两个值分别当成坐标轴上的x和y，坐标点上所对应的value是0或者1。如果把这些数据输入机器学习模型，那么X的两个值代表两个feature，而label便是y了。
复制代码
1
2
3
4
5
6
7
X和y的数据格式：
X= [[-0.93536724 0.69245937]
[ 0.05074294 0.40678444]
[-0.24745421 0.38727354]
[ 0.75084375 -0.44781772]]
y= [1, 0, 1, 1, 1]下面是具体的代码：
首先需要导入包和设置显示窗口的大小
复制代码
1
2
3
4
5
6
7
8
9
# Package imports
import matplotlib.pyplot as plt
import numpy as np
import sklearn.linear_model
import matplotlib
# Display plots inline and change default figure size
matplotlib.rcParams['figure.figsize'] = (6.0, 4.0)
np.random.seed(6)生成月亮形的数据集，其中总共有200个点，并且让数据包含一点噪声
复制代码
1
X, y = sklearn.datasets.make_moons(200, noise=0.20)最后便是绘制散点图。其中X[:, 0]表示获取X中第一列的数据，并把它作为散点图的x轴，X[:, 1]表示获取X第二列的数据并把它作为散点图的y轴。
复制代码
1
2
plt.scatter(X[:, 0], X[:, 1], s=20, c=y, cmap=plt.cm.Spectral)
plt.show()这样之后，就可以顺利绘制一个双月亮形的散点图了。如果要绘制其他形状的图片，那么只需要参考下面的包就可以生成和绘制其他数据了。这些包在sklearn.dataset模块下的_init_.py文件下。如果使用pycharm的话，可以从下面的语句中进去(按住ctrl键，点击datasets)：
复制代码
1
X, y = sklearn.datasets.make_moons(200, noise=0.20)sklearn.dataset模块下的数据生成的方法：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
'clear_data_home',
'dump_svmlight_file',
'fetch_20newsgroups',
'fetch_20newsgroups_vectorized',
'fetch_lfw_pairs',
'fetch_lfw_people',
'fetch_mldata',
'fetch_olivetti_faces',
'fetch_species_distributions',
'fetch_california_housing',
'fetch_covtype',
'fetch_rcv1',
'fetch_kddcup99',
'get_data_home',
'load_boston',
'load_diabetes',
'load_digits',
'load_files',
'load_iris',
'load_breast_cancer',
'load_linnerud',
'load_mlcomp',
'load_sample_image',
'load_sample_images',
'load_svmlight_file',
'load_svmlight_files',
'load_wine',
'make_biclusters',
'make_blobs',
'make_circles',
'make_classification',
'make_checkerboard',
'make_friedman1',
'make_friedman2',
'make_friedman3',
'make_gaussian_quantiles',
'make_hastie_10_2',
'make_low_rank_matrix',
'make_moons',
'make_multilabel_classification',
'make_regression',
'make_s_curve',
'make_sparse_coded_signal',
'make_sparse_spd_matrix',
'make_sparse_uncorrelated',
'make_spd_matrix',
'make_swiss_roll',
'mldata_filename']生成数据的完整代码：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Package imports
import matplotlib.pyplot as plt
import numpy as np
import sklearn
import sklearn.datasets
import sklearn.linear_model
import matplotlib
# Display plots inline and change default figure size
matplotlib.rcParams['figure.figsize'] = (6.0, 4.0)
np.random.seed(6)
X, y = sklearn.datasets.make_moons(200, noise=0.20)
print(X)
print(y)
# X, y = sklearn.datasets.make_circles(200, noise=0.08)
# X, y = sklearn.datasets.make_blobs(200, centers=5)
# X, y = sklearn.datasets.make_regression(n_samples=50,n_features=1, n_targets=1, noise=30)
# plt.scatter(X, y)
plt.scatter(X[:, 0], X[:, 1], s=20, c=y, cmap=plt.cm.Spectral)
plt.show()可视化（绘制）机器学习模型预测之后的结果
但是，如何显示模型训练之后的效果图呢? 比如就像图1-2这样的效果。下面函数使用了下面的算法.
该方法的参数pre_func是模型的预测函数。该函数的思路为：
1. 寻找一个长方体，使它能够完全覆盖所有的点。
2. 把这个长方体分成多个小格子，每个格子的边长为0.01
3. 把格子所在的坐标两个值作为机器学习模型的两个feature，输入pred_func函数中预测，预测函数返回不同的值对应不同的类别，也对应不同的颜色。
4. 在相应的格子里面绘制相应的颜色。
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def plot_decision_boundary(pred_func):
# Set min and max values and give it some padding
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
h = 0.01
# Generate a grid of points with distance h between them
#该函数下面有解释
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
print(len(xx.ravel()), xx.shape, len(yy.ravel()), yy.shape)
# Predict the function value for the whole gid
Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)对np.meshgrid方法的解释：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
In [3]: x = np.arange(4)
In [4]: x
Out[4]: array([0, 1, 2, 3])
In [5]: y = np.arange(5)
In [6]: y
Out[6]: array([0, 1, 2, 3, 4])
In [7]: data_list = np.meshgrid(x, y)
In [8]: data_list
Out[8]:
[array([[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3]]),
array([[0, 0, 0, 0],
[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3],
[4, 4, 4, 4]])]
In [9]: xx, yy = data_list
In [10]: xx
Out[10]:
array([[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3]])
In [11]: yy
Out[11]:
array([[0, 0, 0, 0],
[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3],
[4, 4, 4, 4]])
In [12]: xx.shape
Out[12]: (5, 4)
In [13]: yy.shape
Out[13]: (5, 4)可以明显看出，yy代表y轴，所以数值从上往下递增，xx代表x轴，数值从左往右递增。
结束！谢谢！
附录
本文使用下面的tensorflow代码进行模型预测和图片生成的。
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import numpy as np
import sklearn
import sklearn.datasets
import sklearn.linear_model
import matplotlib
learning_rate = 0.2
num_epoch = 1000;
example_num = 200;
input_node_num = 2;
output_node_num = 5;
def get_case_data(example_num = 200):
np.random.seed(6)
X, y = sklearn.datasets.make_moons(example_num, noise=0.20)
# X, y = sklearn.datasets.make_circles(200, noise=0.08)
# X, y = sklearn.datasets.make_blobs(200, centers=5)
return X, y;
def convert_to_one_hot(y, depth):
return tf.one_hot(y, depth, axis=0).eval()
def process_original_data(X, Y):
X = X.T
Y = convert_to_one_hot(Y, 5)
return X, Y
#
# def display(X, Y):
# matplotlib.rcParams['figure.figsize'] = (6.0, 4.0)
# plt.scatter(X[:, 0], X[:, 1], s=4, c=Y, cmap=plt.cm.Spectral)
# plt.show()
def initialize_parameters():
W1 = tf.get_variable("W1", [6, input_node_num], initializer=tf.contrib.layers.xavier_initializer(seed=1))
b1 = tf.get_variable("b1", [6, 1], initializer=tf.zeros_initializer())
W2 = tf.get_variable("W2", [8, 6], initializer=tf.contrib.layers.xavier_initializer(seed=1))
b2 = tf.get_variable("b2", [8, 1], initializer=tf.zeros_initializer())
W3 = tf.get_variable("W3", [output_node_num, 8], initializer=tf.contrib.layers.xavier_initializer(seed=1))
b3 = tf.get_variable("b3", [output_node_num, 1], initializer=tf.zeros_initializer())
result = {'W1':W1, 'b1':b1, 'W2':W2, 'b2':b2, 'W3':W3, 'b3':b3}
return result
def forward_propagate(X, parameters):
X = tf.cast(X, np.float32)
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
W3 = parameters['W3']
b3 = parameters['b3']
### START CODE HERE ### (approx. 5 lines) # Numpy Equivalents:
Z1 = tf.add(tf.matmul(W1, X), b1) # Z1 = np.dot(W1, X) + b1
A1 = tf.nn.relu(Z1) # A1 = relu(Z1)
Z2 = tf.add(tf.matmul(W2, A1), b2) # Z2 = np.dot(W2, a1) + b2
A2 = tf.nn.relu(Z2) # A2 = relu(Z2)
Z3 = tf.add(tf.matmul(W3, A2), b3)
return Z3
def compute_cost(Z3, y):
logits = tf.transpose(Z3)
labels = tf.transpose(y)
return tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=labels))
def predict(X, parameters):
y_hat = forward_propagate(X, parameters)
y_hat = tf.transpose(y_hat)
y_hat = tf.nn.softmax(logits=y_hat)
return y_hat
def plot_decision_boundary(X, y, pred_func):
# Set min and max values and give it some padding
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole gid
Z = pred_func(np.c_[xx.ravel(), yy.ravel()])#
Z = Z.eval() # 因为Z是一个tensorflow对象，所以需要调用eval方法
Z = np.argmax(Z, axis=1)
Z = np.reshape(Z, xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, s=20, cmap=plt.cm.Spectral)
X_original, Y_original = get_case_data(example_num)
def build_model(X_original, Y_original):
X = tf.placeholder(dtype=tf.float32, shape=(input_node_num, None), name='X')
Y = tf.placeholder(dtype=tf.float32, shape=(output_node_num, None), name='y')
parameters = initialize_parameters();
y_hat = forward_propagate(X, parameters=parameters)
cost = compute_cost(y_hat, Y)
train = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
X_train, Y_train = process_original_data(X_original, Y_original)
for i in range(num_epoch):
_, training_cost = sess.run([train, cost], feed_dict={X: X_train, Y: Y_train})
if i % 10 == 0:
print(training_cost)
correct_prediction = tf.equal(tf.argmax(y_hat), tf.argmax(Y))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, dtype="float"))
print("Train Accuracy:", accuracy.eval({X: X_train, Y: Y_train}))
parameters = sess.run(parameters)
def do_predict(X):
return predict(X.T, parameters)
matplotlib.rcParams['figure.figsize'] = (5.0, 4.0)
plot_decision_boundary(X_original, Y_original, lambda x: do_predict(x))
plt.title("model")
plt.show()
build_model(X_original, Y_original)1
1
1
1
1
1
最后
以上就是敏感手套最近收集整理的关于深度学习1：生成模型的输入数据集和可视化的全部内容，更多相关深度学习1：生成模型内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复