从例子开始学隐马尔可夫模型，是一个较为简单的学习方法。

1.啥也不说，先看个例子

我面前有个桌子，桌子上有5个外观一模一样的盒子，按照一排摆放，每个盒子里面都装有10个形状大小一模一样的圆球，每个球只能是红色或者白色，下面是每个盒子装有球的信息.

1.1盒子信息

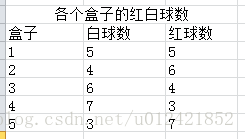
轻松得到如下信息：

    盒子集合={盒子1，盒子2，盒子3，盒子4，盒子5}

    球颜色集合={白色，红色}

    从每个盒子当中随机取出一个球，是红球和白球的概率为：

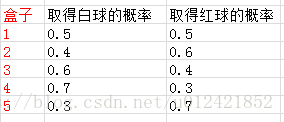
现在，我们开始做个游戏：从这些盒子里面取n次球，每次随机取1个球并记录球的颜色，然后再将球放入原来所在盒子，再按照给定规则从后续的盒子重复上述动作，直到取够n次球。

给定规则由1.2当前盒子到下个盒子的规则给出。

1.2当前盒子到下个盒子的规则

我给游戏定了一个规则：

    假如当前从盒子1里面取1个球，则下次必须从盒子2里面取1个球；

    假如当前从盒子2里面取1个球，则下次以0.6的概率从其左边盒子里面取1个球，以0.4的概率从其右边盒子里面取1个球；

    假如当前从盒子3里面取1个球，则下次以0.4的概率从其左边盒子里面取1个球，以0.6的概率从其右边盒子里面取1个球；

    假如当前从盒子4里面取1个球，则下次以0.5的概率从盒子2里面取1个球，以0.5个概率从盒子5里面取1个球；

    假如当前从盒子5里面取1个球，则下次以0.3的概率从盒子1里面取1个球，以0.7的概率从盒子3里面取1个球；

这个从当前盒子到下个盒子的规则，用表格表示出来如下所示：

可以知道，如果当前盒子是第一个盒子时，以相同的概率从5个盒子里面取球，所以每个盒子在第一次被取到的概率都是1/5

每个盒子是第一个盒子的概率为：

2.隐马尔可夫模型的概念

2.1隐马尔可夫模型的定义

    隐马尔可夫模型（Hidden Markov Model，HMM）是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。

    隐藏的马尔可夫链随机生成的状态的序列，称为状态序列（state sequence）

    每个状态生成一个观测，而由此生成的观测的随机序列，称为观测序列(obervation sequence)

    序列的每个位置又可以看做一个时刻。

从上面的游戏来理解隐马尔科夫模型：

对于上面的游戏中，假如n=6，游戏过后我们得到一个球的颜色的观测序列为：O={红，白，红，红，白，红}

如果仅仅知道观测序列O，而在游戏过程中不知道取球的整个过程中盒子序列，即不知道每个球是从哪个盒子中取出来的！

我们记：盒子的序列为状态序列，球的颜色观测序列为观测序列。

在这个游戏中，状态序列式隐藏不可知的，只有观测序列是可知的。

上面这个游戏这就是一个隐马尔可夫模型的例子~

从这个游戏当中，给出隐马尔可夫模型中的一些基本概念：

2.2所有的状态集合

    Q={盒子1，盒子2，盒子3，盒子4，盒子5}，N=5表示所有可能的状态数

2.3所有的观测集合

    V={红，白}，M=2表示所有可能的观测数

2.4初始状态概率分布

    π=(0.2, 0.2, 0.2, 0.2, 0.2)T，注：T表示转置

    其中第i个概率表示第i个盒子被选做第一个盒子的概率~

2.5状态转移概率分布

就是由当前盒子确定下个盒子的转移概率分布：

A=[ 0        1        0        0        0

      0.6      0        0.4     0        0

      0         0.4     0        0.6     0

      0         0.5     0        0        0.5            

      0.3        0      0.7     0         0]

2.6初始观测概率分布

    说明第i行第1个值表示第i个盒子取出白球的概率，第i行第2个值表示第i个盒子取出红球的概率

    B=[0.5    0.5

          0.4    0.6

          0.6    0.4

          0.7    0.3

          0.3    0.7]

2.7状态序列

    隐藏的马尔科夫链随机生成的状态的序列，成为状态序列(state sequence)

    在上面游戏中来讲的话，安装游戏规则得到的几个盒子组成的一个序列，就是一个状态序列，即一个有n个盒子的序列是一个状态序列。

    I=(盒子1, 盒子2, 盒子3, 盒子4, 盒子5, 盒子3)

2.8观测序列

    每个状态会生成一个观测，而由此产生的观测的随机序列，成为观测序列(observation sequence)，序列的每个位置又可以看做一个时刻。

    比如在上面游戏中我们假设n=6，即我们按照状态转移概率分布依次从6个盒子中取出一个球（取后记录球颜色，然后放入当前盒子），得到如下的颜色序列：

    O={红，白，红，红，白，红}

    则上面这个颜色的序列就是一个观测序列，此观测序列的长度为6.

3.隐马尔科夫模型的确定表示

    隐马尔科夫模型由以下三个对象确定：

        1）初始概率分布π

        2）状态转移概率分布A

        3）观测概率分布B

    因此隐马尔科夫模型λ可以用三元符号表示：

λ=(A, B, π)

    从上面游戏理解的话，如下所示：

        1）初始概率分布

            π=(0.2, 0.2, 0.2, 0.2, 0.2)T，注：T表示转置，其中第i个概率表示第i个盒子被选做第一个盒子的概率~

        2）状态转移概率分布    就是由当前盒子确定下个盒子的转移概率分布：

            A=[ 0        1        0        0        0

                  0.6      0        0.4     0        0

                  0         0.4     0        0.6     0

                  0         0.5     0        0        0.5            

                  0.3        0      0.7     0         0]

        3）观测概率分布    比如刚开始时，初始观测概率分布。说明第i行第1个值表示第i个盒子取出白球的概率，第i行第2个值表示第i个盒子取出红球的概率

        B=[0.5    0.5

              0.4    0.6

              0.6    0.4

              0.7    0.3

              0.3    0.7]

    那么可以知道这个游戏对应的隐马尔科夫模型λ可以表示为：λ=(A, B, π)

3.观测序列的生成过程

    根据隐马尔科夫模型的定义，可以将一个长度为T的观测序列O=（o1, o2, ……，oT）的生成过程描述如下：

    输入：隐马尔科夫模型λ=(A, B, π)，观测序列长度T;

    输出：观测序列O=(o1, o2，……，oT)

    （1）安装初始状态分布π产生状态i1

    （2）令t=1

    （3）根据观测概率分布生成ot

    （4）根据状态转移概率分布生成第t+1状态

    （5）命令t=t+1，如果t<T，转步骤（3）；否则，终止

4.隐马尔可夫模型的三个基本问题

隐马尔科夫模型的3个基本问题：

    4.1概率计算问题

    已知隐马尔科夫模型λ=(A, B, π)

    给定一个观测序列O=(o1, o2, ……，oT)

    问题：计算在模型λ下观测序列O出现的概率P(O|λ)

    4.2学习问题

    已知：一个观测序列O=(o1, o2, ……，oT)

    问题：请估计隐马尔科夫模型λ=(A, B, π)的参数，使得在该模型下观测序列概率P(O|λ)最大

    注：即用最大似然估计的方法估计参数

    4.3预测问题

    也称为解码(decoding)问题。

    已知隐马尔科夫模型λ=(A, B, π)，一个观测序列O=(o1, o2, ……，oT)

    问题：求给定观测序列条件概率P(I|O)最大的状态序列I=(i1, i2, ……，iT)

    注：即给定模型λ和观测序列O，求最有可能的对应的状态序列。

5.参考文档

[1]《统计学习方法》李航.

最后

以上就是欣慰蚂蚁为你收集整理的【机器学习】【隐马尔可夫模型-1】基本概念+观测序列的生成算法+示例讲解2.隐马尔可夫模型的概念3.隐马尔科夫模型的确定表示3.观测序列的生成过程4.隐马尔可夫模型的三个基本问题5.参考文档的全部内容，希望文章能够帮你解决【机器学习】【隐马尔可夫模型-1】基本概念+观测序列的生成算法+示例讲解2.隐马尔可夫模型的概念3.隐马尔科夫模型的确定表示3.观测序列的生成过程4.隐马尔可夫模型的三个基本问题5.参考文档所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。