损失函数与正则项之间的关系和分析

　　

　　看了知乎一篇博文当我们优化损失函数时，我们在优化什么收获良多，对机器学习分类和回归中损失函数和正则项也有了更深的认识。理解了这些，可以加深对逻辑回归，Softmax,线性回归等机器学习方法的理解，知道为什么要这样。现简单总结一下。

　　贝叶斯公式：$p(x|y)=frac{p(y|x)p(x)}{p(y)}$

　　如果设训练集为$D$，那么对于模型参数$w$来说，贝叶斯公式为：$p(w|D)=frac{p(D|w)p(w)}{p(D)}$。

　　其中$p(w)$表示的是参数$w$的先验（prior）分布；$p(D|w)$ 给定参数为$w$的情况下，训练数据为$D$的可能性，我们也可以把它看成一个关于$w$的函数，这个函数叫做似然函数（likelihood function）；$p(w|D)$ 是参数$w$在给定数据$D$下的后验（posterior）分布。

　　给定这些定义，贝叶斯公式可以表示成：$text{posterior }infty text{ likelihood }times text{ prior}$，即后验正比于似然乘以先验。

　　通过极大似然函数$p(D|w)$，我们可以找到一个最优的参数$w^*$，使得在这组参数设定下，出现训练数据$D$的可能性$p(w|D)$ 最大。这组参数在统计上叫做参数$w$的极大似然估计。

　　对上式贝叶斯公式两边取对数，可得：$text{In }p(w|D)=text{In }p(D|w)+text{In }p(w)+const$。

　　可以看出，加入正则项相当于加入了$w$的的先验分布$p(w)$。

 

　　回归与分类问题的损失函数分析

　　在回归问题（regression problems）中，常用平方误差和（sum of squares）来衡量模型的好坏。给定一个包含$N$个数据的训练集 $x={x_1,x_2,...,x_N}$ ，以及这些数据对应的目标值 $t={t_1,t_2,...,t_N}$，回归问题的目标是利用这组训练集，寻找一个合适的模型，来预测一个新的数据点$hat{x}$对应的目标值$hat{t}$。记模型的参数为$w$，模型对应的函数为$y$ ，模型的预测值可以相应表示为 $y(x,w)$。

　　为了衡量模型的好坏，需要一种方法衡量预测值与目标值之间的误差，一个常用的选择是平方误差和：

　　[E(w)=frac{1}{2}sumlimits_{n=1}^{N}{left{ y({{x}_{n}},w)-{{t}_{n}} right}}] 

　　回归问题的目标是找到一组参数$w^*$使得误差函数$E(w)$最小化。而最小化$E(w)$的意思是什么呢？

　　误差会来自两个部分：系统误差和随机误差。通过多次测量能够减少随机误差，但是不能减少系统误差，所以测量误差是不可避免的。同理，在回归问题中，$x$的测量值$t$也会存在一定的误差。假定对所有的数据点$x$，模型预测值 与目标值 $t$之间的误差是一样的，并服从一定的概率分布，比如均值为0，方差为 ${{beta }^{-1}}={{sigma }^{2}}$的高斯分布，则有：

[p(t-y(x,w)|x,w,beta )tilde{ }mathcal{N}(t-y(x,w)|0,{{beta }^{-1}})]

即：$p(t|x,w,beta )tilde{ }mathcal{N}(t|y(x,t),{{beta }^{-1}})$

　　对于一组独立同分布的数据点  $x={x_1,x_2,...,x_N}$ ，以及这些数据对应的目标值 $t={t_1,t_2,...,t_N}$，我们得到关于这组数据的似然函数：

　　[p(t|x,w,{{beta }^{-1}})=prodlimits_{n=1}^{N}{p}({{t}_{n}}|{{x}_{n}},w,{{beta }^{-1}})=prodlimits_{n=1}^{N}{mathcal{N}}({{t}_{n}}|y({{x}_{n}},w),{{beta }^{-1}})]

　　其中，高斯分布的概率函数为：

　　[N(t|y(x,t),{{beta }^{-1}})={{left( frac{beta }{2pi } right)}^{frac{1}{2}}}exp left{ -frac{beta }{2}{{left[ t-y(x,w) right]}^{2}} right}]

　　可以通过极大化这个似然函数得到关于 的一组极大似然解。不过，更方便的做法是极大对数似然函数，因为对数函数是严格单增的，所以极大对数似然的解与极大似然的解是相同的。

　　对数似然函数为：

[ln p(t|x,w,{{beta }^{-1}})=-frac{beta }{2}sumlimits_{n=1}^{N}{{y(}{{x}_{n}},w)-t{{}}^{2}}+frac{N}{2}ln beta -frac{N}{2}ln 2pi ]

如果我们不考虑 $beta $ 的影响，那么，对于参数 $w$来说，最小化平方误差和的解，就等于极大对数似然的估计。因此，最小化平方误差和 $E(W)$ 与极大似然等价，考虑到似然函数的定义，优化 $E(W)$ 相当于在给定高斯误差的假设下，寻找一组 $w$ 使得观察到目标值$t$的概率最大。

 

　　在分类问题中，给定一个包含$N$个数据样本的训练集 $x={x_1,x_2,...,x_N}$ ，以及这些数据对应的类别$t={t_1,t_2,...,t_N}$，这里， ${{t}_{n}}in {1,2,ldots ,K}$，分类问题的目标是利用这组训练集，寻找一个合适的模型，来预测一个新的数据点$hat{x}$对应的类别$hat{t}$。现在假设模型的参数为$w$，模型输出是属于每一类的概率，预测为第 $kin {1,2,ldots ,K}$ 类的概率为$p(k|x,w)$ 。

对于样本 $x$，其属于第$t$类的概率为：[p(t|x,w)=prodlimits_{k=1}^{K}{p}{{(y=t|x,w)}^{{{1}_{t=k}}}}]

其中，。

因此，似然函数为：$p(t|x,w)=prodlimits_{n=1}^{N}{(prodlimits_{k=1}^{K}{p}{{({{t}_{n}}|{{x}_{n}},w)}^{{{1}_{t=k}}}})}$

对数似然为：$ln p(t|x,w)=sumlimits_{n=1}^{N}{sumlimits_{k=1}^{K}{{{1}_{t=k}}}}log p({{t}_{n}}|{{x}_{n}},w)$

极大化对数似然，相当于极小化：$-sumlimits_{n=1}^{N}{sumlimits_{k=1}^{K}{{{1}_{t=k}}}}log p({{t}_{n}}|{{x}_{n}},w)$

事实上，这正是我们常使用的多类交叉熵损失函数的表示形式。

因此，在分类问题中，最小化交叉熵损失函数相当与极大样本的似然函数。  可以联系逻辑回归于softmax的损失函数，其极大似然函数就是交叉熵损失函数。

 

　　正则项

 

在优化目标函数时，除了正常的损失函数外，为了防止过拟合，我们通常会加入一些正则项。由上面的分析可知，加入正则项，相当于给参数$w$加入了其先验分$p(w)$。常见的正则项有L0、L1和L2正则。

• L0正则是向量的0范数，指向量中非零元素的个数。L0正则化的值是模型中非零参数的个数，L0正则化可以实现模型参数的的稀疏化，然然L0正则化是个NP难问题，很难求解，一般使用L1正则实现参数的稀疏化。
• L1正则是向量的1范数，指向量各元数绝对值的和。L1正则可以使参数更多的等于0，故可以实现参数的稀疏，也叫做Lasso回归。
• L2正则是向量的2范数，指向量的内积，是所有元素的平方和在求平方根。L2正则可以使参数都趋向于0，故可以实现参数的平滑，也叫Ridge回归

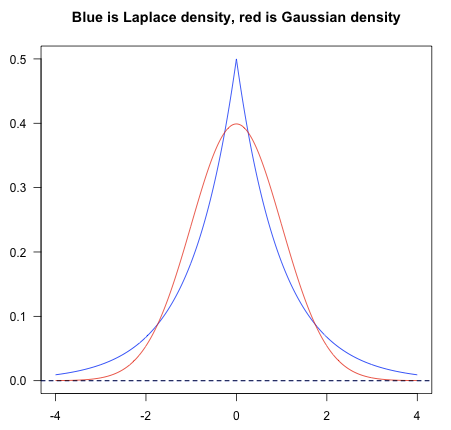
　　给损失函数加入正则项相当于加入了对参数的先验分布，因而能防止过拟合。其中，L1正则等价于参数$w$的先验分布满足均值为0的拉普拉斯分布，均值为0的拉普拉斯在0附近突出，周围稀疏，对应容易产生稀疏解的模型；L2正则等价于参数w的先验分布满足均值为0的正态分布，均值为0的正态分布在0附近平滑，对应容易产平滑解的模型。