独立集

在无向图里面，使得任意两点之间没有一条连边。如果拥有集合中点最多的话就是最大独立集。
且如果在二分图里，最大独立集 = n - 最大匹配数。

Garden

在一张四连通的网格图里，想要分成二分图的话，以点的（x+y）判断奇偶确定在左边还是右边。以矛盾作为它的边，跑一次最大匹配，独立集等于 n - 最大匹配数

然后要把最大独立集的点都打出来，那么刚开始被选入二分图匹配但是没有流量经过的点一定是独立集里面的点，这时候我的朋友进入了一个错误的想法就是只打出一边的点和另一边（无流量经过）的点

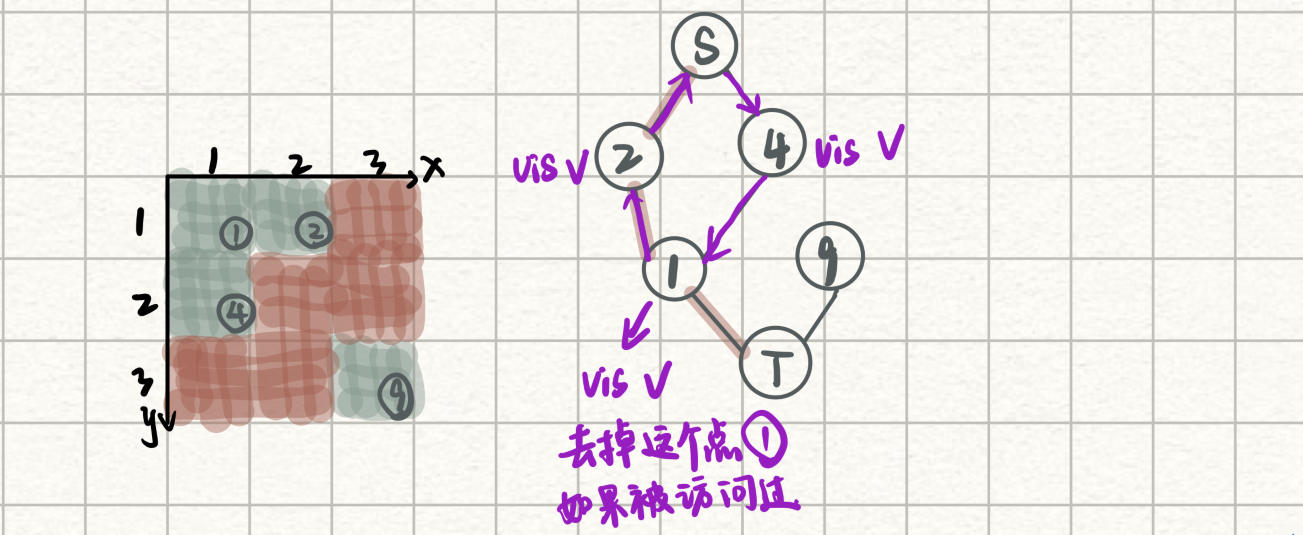
就像上面的情况打出的集合不能是{ 1 , 4 , 9 } 而只能是{ 2 , 4 , 9 }这个集合
因为{ 1 , 4 }之间存在连边会使答案矛盾

#include<bits/stdc++.h>
using namespace std;
const int maxn = 101000, maxm = 500000;
const int INF = 0x3f3f3f3f;
struct edge {
	int u, v, cap, flow;
	edge() {}
	edge(int u, int v, int cap, int flow) :u(u), v(v), cap(cap), flow(flow) {}
}eg[maxm << 1];
int tot, dis[maxn << 1], cur[maxn << 1];
vector<int> tab[maxn << 1];
void init(int n) {
	tot = 0;
	while (n)tab[n--].clear();
	tab[0].clear();
}
void addedge(int u, int v, int cap) {
	tab[u].push_back(tot);
	eg[tot++] = edge(u, v, cap, 0);
	tab[v].push_back(tot);
	eg[tot++] = edge(v, u, 0, 0);
}
int bfs(int s, int t) {
	queue<int> q;
	q.push(s);
	memset(dis, INF, sizeof dis);
	dis[s] = 0;
	while (!q.empty()) {
		int h = q.front(), i;
		q.pop();
		for (i = 0; i < tab[h].size(); i++) {
			edge& e = eg[tab[h][i]];
			if (e.cap > e.flow && dis[e.v] == INF) {
				dis[e.v] = dis[h] + 1;
				q.push(e.v);
			}
		}
	}
	return dis[t] < INF;
}
int dfs(int x, int maxflow, int s, int t) {
	if (x == t || maxflow == 0)
		return maxflow;
	int flow = 0, i, f;
	for (i = cur[x]; i < tab[x].size(); i++) {
		cur[x] = i;
		edge& e = eg[tab[x][i]];
		if (dis[e.v] == dis[x] + 1 && (f = dfs(e.v, min(maxflow, e.cap - e.flow), s, t)) > 0) {
			e.flow += f;
			eg[tab[x][i] ^ 1].flow -= f;
			flow += f;
			maxflow -= f;
			if (maxflow == 0)
				break;
		}
	}
	return flow;
}
int dinic(int s, int t) {
	int flow = 0;
	while (bfs(s, t)) {
		memset(cur, 0, sizeof(cur));
		flow += dfs(s, INF, s, t);
	}
	return flow;
}
string ss[maxn]; int vis[maxn];
int main() {
	int n, m;
	cin >> n >> m;
	init(n * m + 3);
	int s = n * m + 1;
	int t = n * m + 2;
	for (int i = 1; i <= n; i++) {
		cin >> ss[i];
	}
	int cnt = 0;
	for (int i = 1; i <= n; i++) {
		for (int j = 0; j < m; j++) {
			if (ss[i][j] == '*') continue;
			cnt++;
			if ((i + j) % 2 == 0) {
				addedge(s, (i - 1) * (m)+j, 1);
				if (i + 1 <= n && ss[i + 1][j] == '.') addedge((i - 1) * (m)+j, i * m + j, 1);
				if (i - 1 > 0 && ss[i - 1][j] == '.') addedge((i - 1) * (m)+j, (i - 2) * m + j, 1);
				if (j + 1 < m && ss[i][j + 1] == '.') addedge((i - 1) * m + j, (i - 1) * m + j + 1, 1);
				if (j - 1 >= 0 && ss[i][j - 1] == '.') addedge((i - 1) * m + j, (i - 1) * m + j - 1, 1);
			}
			else {
				addedge((i - 1) * (m)+j, t, 1);
			}
		}
	}
	cout << cnt - dinic(s, t) << endl;
	queue<int>qwq;
	qwq.push(s);
	vis[s] = 1;
	while (!qwq.empty()) {
		int u = qwq.front();
		qwq.pop();
		for (int i = 0; i < tab[u].size(); i++) {
			edge& e = eg[tab[u][i]];
			int v = e.v;
			if (!vis[v] && (e.cap-e.flow)) {
				qwq.push(v); vis[v] = 1;
			}
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 0; j < m; j++) {
			if (ss[i][j] == '*') continue;
			if (((i + j) % 2) == 0) {
				if (vis[(i - 1) * m + j]) ss[i][j] = 'C';
			}
			else {
				if (!(vis[(i - 1) * m + j])) ss[i][j] = 'C';
			}

		}
	}
	for (int i = 1; i <= n; i++) {
		cout << ss[i] << endl;
	}
	return 0;
}

最后

以上就是清脆向日葵为你收集整理的最大独立集Garden的全部内容，希望文章能够帮你解决最大独立集Garden所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。