概述
目录
一，特征压缩搜索
二，正方形骨牌覆盖问题
1，数字最小化
2，是否可翻转
3，生成骨牌的所有形态
4，求解
三，覆盖问题的特征压缩搜索
一，特征压缩搜索
以一个简单的问题为例。
有4个党支部，分别有20人，20人，10人，10人。
现在要安排30人去A影厅看电影，安排30人去B影厅看电影，但是同一党支部的人必须在同一个电影院。
每个影厅的座位号都是从1到30编号，这4个党支部的人分别来自10个项目组，对应关系为balabala，略。
问题一：为了让每个项目组的人都尽量编号相近，评价方法为损失函数f=balabala，略，应该怎么安排？
问题二：为了让每个人都尽量与别的项目组的人坐一起，评价方法为损失函数g=balabala，略，应该怎么安排？
由于这个问题非常简单，所以第一步很显然是如何安排党支部和影厅的对应关系，本题中有4种对应关系。
然后第二步才是，基于每一种对应关系，搜索最优解。
如果问题变成，党支部有100个，每个党支部有3-5人，那么第一步就没那么明显了，但是实际上仍然比最暴力的方法要好。
最暴力的搜索方法可能是，枚举所有人的每一个全排列，取其中最优解。
言归正传，对于这种搜索问题，我们提取一个特征，使得问题简化成子问题，子问题的解空间是原问题的解空间的退化，那么我们先搜索子问题的解，这样就相当于把原问题做了剪枝，通常情况下把绝大部分情况都剪掉了。
二，正方形骨牌覆盖问题
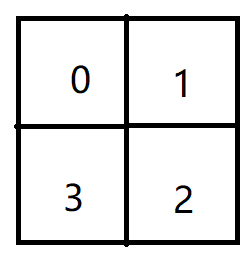
有正方形四格骨牌若干，每张骨牌四格格子都有一个自然数，骨牌可以旋转，要求这些骨牌怎么放，使得四个格子的总数等于给定的数。
一般这种问题有两种，可以翻转的居多，不能翻转的也有。
1，数字最小化
如果每个数都大于0，那么四个格子全都减掉一个数，总数也减掉这个数即可。
所以问题可以化成，每个格子至少有1个是0，剩下的3个都是自然数。
如果4个格子都是0，那么这个骨牌就不需要参与计算了。
否则，这个骨牌旋转得到的4种情况一定都不一样。
2，是否可翻转
对于一些骨牌，能不能翻转都是一样的，判断方法就是看这个骨牌是不是对称的，其中对称轴有米字四线四种情况。
bool needOverturn(vector<int> v)
{
if (v[0] == v[1] && v[2] == v[3])return false;
if (v[1] == v[2] && v[0] == v[3])return false;
return v[0] != v[2] && v[1] != v[3];
}3，生成骨牌的所有形态
如果能翻转，那么对于可翻转骨牌，就有8种形态，其他骨牌有4种形态。
如果不能翻转自然都只有4种形态。
vector<vector<int>> overturn(vector<int> v)
{
vector<vector<int>> ans(0);
for (int i = 0; i < 4; i++) {
ans.push_back(v);
v.push_back(v[0]);
v.erase(v.begin());
}
if (!needOverturn(v))return ans;
v[0] ^= v[2] ^= v[0] ^= v[2];
for (int i = 0; i < 4; i++) {
ans.push_back(v);
v.push_back(v[0]);
v.erase(v.begin());
}
}4，求解
完整代码：
#include<iostream>
#include <vector>
using namespace std;
vector<vector<int>>num =
{
{2,2,1,0},
{2,2,1,0},
{2,2,1,0},
{2,2,1,0},
{1,0,0,0},
{1,0,0,0},
{2,2,0,0},
{3,1,0,1},
{2,1,0,1},
};
vector<int> s = { 10,9,7,9 };
const bool canOverturn = true;
bool needOverturn(vector<int> v)
{
if (v[0] == v[1] && v[2] == v[3])return false;
if (v[1] == v[2] && v[0] == v[3])return false;
return v[0] != v[2] && v[1] != v[3];
}
vector<vector<int>> overturn(vector<int> v)
{
vector<vector<int>> ans(0);
for (int i = 0; i < 4; i++) {
ans.push_back(v);
v.push_back(v[0]);
v.erase(v.begin());
}
if (!needOverturn(v) || !canOverturn)return ans;
v[0] ^= v[2] ^= v[0] ^= v[2];
for (int i = 0; i < 4; i++) {
ans.push_back(v);
v.push_back(v[0]);
v.erase(v.begin());
}
return ans;
}
bool ok(const vector<vector<int>> &v)
{
for (int i = 0; i < s.size(); i++)
{
int k = s[i];
for (auto& vi : v)k -= vi[i];
if (k)return false;
}
return true;
}
void out(vector<int>v)
{
for (auto& vi : v)cout << vi << " ";
cout << endl;
}
void out(vector<vector<int>>v)
{
for (auto& vi : v)out(vi);
cout << endl << endl;
}
int main()
{
vector<vector<vector<int>>> dom(0);
for (auto &vi : num)dom.push_back(overturn(vi));
int s = 1;
for (auto& vi : dom)s *= vi.size();
cout << s;
int ansnum = 0;
for (int i = 0; i < s; i++)
{
vector<vector<int>>vd;
int k = i;
for (int j = dom.size() - 1; j >= 0; j--)
{
vd.push_back(dom[j][k % dom[j].size()]);
k /= dom[j].size();
}
if (ok(vd)) {
//out(vd);
ansnum++;
if (ansnum % 100 == 0)cout << ansnum << " ";
}
}
cout << ansnum;
return 0;
}解空间有4194304，满足条件的有26412。
如果canOverturn = false，解空间有262144，满足条件的解有1642。
三，覆盖问题的特征压缩搜索
1，骨牌表示
有格子的是1，空出来的是0
vector<vector<int>> block[] =
{
{
{1,1,1,1}
},
{
{1,0,1},
{1,1,1}
},
{
{1,1,0},
{0,1,0},
{0,1,1}
},
{
{1,1,0},
{1,1,1}
},
{
{1,0,0,0},
{1,1,1,1}
},
{
{1,0,0},
{1,1,1}
},
{
{0,1,0},
{0,1,0},
{1,1,1}
},
{
{1,1,0,0},
{0,1,1,1}
},
{
{1,0,0},
{1,0,0},
{1,1,1}
},
{
{1,1,0},
{0,1,1}
}
};2，生成骨牌的所有形态
普通骨牌可以旋转四次，对于中心对称的骨牌只需要旋转两次。
有的骨牌需要翻转，有的骨牌不需要（左右对称或者上下对称）。
于是，不同的骨牌可能有1,2,4,8种不同形态。
由于这个拼图没有正方形，所以没有只有一种形态的骨牌。
int blockNum = 10;
int needOverturn[] = { 0,0,1,1,1,1,0,1,0,1};
int needRotation[] = { 2,4,2,4,4,4,4,4,4,2 };
//翻转vector
template<typename T>
vector<T> frev(const vector<T>& v)
{
vector<T> ans;
ans.resize(v.size());
for (int i = 0; i < v.size(); i++)ans[i] = v[v.size() - 1 - i];
return ans;
}
//翻转二维vector的每一行
template<typename T>
vector<vector<T>> frev(const vector<vector<T>>& v)
{
vector<vector<T>>ans;
for (int i = 0; i < v.size(); i++)ans.push_back(frev(v[i]));
return ans;
}
//沿主对角线翻转二维vector
template<typename T>
vector<vector<T>> foverturn(const vector<vector<T>>& v)
{
vector<vector<T>> ans(v[0].size());
for (int i = 0; i < v[0].size(); i++) {
ans[i].resize(v.size());
for (int j = 0; j < v.size(); j++)ans[i][j] = v[j][i];
}
return ans;
}
//顺时针旋转二维vector
template<typename T>
vector<vector<T>> frotation(const vector<vector<T>>& v)
{
return frev(foverturn(v));
}
//得到骨牌的所有形态
vector<vector<vector<int>>> overturnOrRotation(int k)
{
vector<vector<vector<int>>> ans(0);
vector<vector<int>> vt = block[k];
for (int i = 0; i < needRotation[k]; i++) {
ans.push_back(vt);
vt = frotation(vt);
}
vt = foverturn(vt);
for (int i = 0; i < needRotation[k]; i++) {
ans.push_back(vt);
vt = frotation(vt);
}
return ans;
}3，特征压缩
覆盖问题可以提取特征，化成子问题——正方形骨牌覆盖问题。
采用奇偶染色法，任意骨牌都可以化成正方形四格骨牌，四格格子都有一个自然数。
例如：
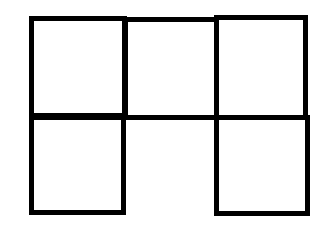
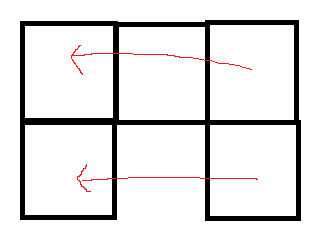
这样就得到：
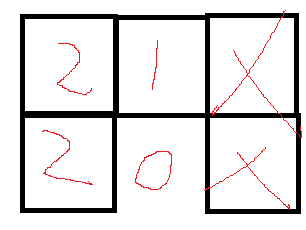
按照上面的编号方式来转换就是 2 1 0 2，如果旋转90度就变成 2 2 1 0
vector<int> shrink(const vector<vector<int>>& v)
{
vector<int> ans(4);
for (int i = 0; i < v.size(); i++) {
for (int j = 0; j < v[0].size(); j++) {
ans[(i % 2 == 0) ? j % 2 : 3 - j % 2] += v[i][j];
}
}
return ans;
}如果按照正常顺序来编号，那就是
vector<int> shrink(const vector<vector<int>>& v)
{
vector<int> ans(4);
for (int i = 0; i < v.size(); i++) {
for (int j = 0; j < v[0].size(); j++) {
ans[i % 2 * 2 + j % 2] += v[i][j];
}
}
return ans;
}4，完整代码
先生成所有压缩形态，再生成所有形态和相位组合（最多32个）对应的压缩形态id
根据压缩形态的解，散开成本位解
//#include "t.h"
#include<iostream>
#include <vector>
using namespace std;
vector<vector<int>> block[] =
{
{
{1,1,1,1}
},
{
{1,0,1},
{1,1,1}
},
{
{1,1,0},
{0,1,0},
{0,1,1}
},
{
{1,1,0},
{1,1,1}
},
{
{1,0,0,0},
{1,1,1,1}
},
{
{1,0,0},
{1,1,1}
},
{
{0,1,0},
{0,1,0},
{1,1,1}
},
{
{1,1,0,0},
{0,1,1,1}
},
{
{1,0,0},
{1,0,0},
{1,1,1}
},
{
{1,1,0},
{0,1,1}
}
};
vector<vector<vector<int>>> shrinkBlocks;
vector<int> shrinkSum = { 14,12,11,10};
const int blockNum = 10;
int needOverturn[] = { 0,0,1,1,1,1,0,1,0,1 };
int needRotation[] = { 2,4,2,4,4,4,4,4,4,2 };
vector<int> shrink(const vector<vector<int>>& v)
{
vector<int> ans(4);
for (int i = 0; i < v.size(); i++) {
for (int j = 0; j < v[0].size(); j++) {
ans[i % 2 * 2 + j % 2] += v[i][j];
}
}
return ans;
}
//翻转vector
template<typename T>
vector<T> frev(const vector<T>& v)
{
vector<T> ans;
ans.resize(v.size());
for (int i = 0; i < v.size(); i++)ans[i] = v[v.size() - 1 - i];
return ans;
}
//翻转二维vector的每一行
template<typename T>
vector<vector<T>> frev(const vector<vector<T>>& v)
{
vector<vector<T>>ans;
for (int i = 0; i < v.size(); i++)ans.push_back(frev(v[i]));
return ans;
}
//沿主对角线翻转二维vector
template<typename T>
vector<vector<T>> foverturn(const vector<vector<T>>& v)
{
vector<vector<T>> ans(v[0].size());
for (int i = 0; i < v[0].size(); i++) {
ans[i].resize(v.size());
for (int j = 0; j < v.size(); j++)ans[i][j] = v[j][i];
}
return ans;
}
//顺时针旋转二维vector
template<typename T>
vector<vector<T>> frotation(const vector<vector<T>>& v)
{
return frev(foverturn(v));
}
//得到骨牌的所有形态
vector<vector<vector<int>>> overturnOrRotation(int k)
{
vector<vector<vector<int>>> ans(0);
vector<vector<int>> vt = block[k];
for (int i = 0; i < needRotation[k]; i++) {
ans.push_back(vt);
vt = frotation(vt);
}
if (needOverturn[k] == 0)return ans;
vt = foverturn(vt);
for (int i = 0; i < needRotation[k]; i++) {
ans.push_back(vt);
vt = frotation(vt);
}
return ans;
}
// 生成枚举序号
template<typename T>
vector<vector<int>> foreach(const vector<vector<T>>&v)
{
int s = 1;
for (auto& vi : v)s *= vi.size();
vector<vector<int>> ans(s);
while (--s)
{
ans[s].resize(v.size());
int st = s;
for (int j = v.size() - 1; j >= 0; j--)
{
ans[s][j] = st % v[j].size();
st /= v[j].size();
}
}
return ans;
}
void jian(vector<int>&v, const vector<int> &v2)
{
for (int i = 0; i < v.size(); i++)v[i] -= v2[i];
}
bool allZero(const vector<int> &v)
{
for (auto &vi : v)if (vi)return false;
return true;
}
bool ok(const vector<int>& v)
{
vector<int> st = shrinkSum;
for (int i = 0; i < blockNum; i++)
{
jian(st, shrinkBlocks[i][v[i]]);
}
return allZero(st);
}
int main()
{
vector<vector<vector<vector<int>>>> blocks;
for (int i = 0; i < blockNum; i++)
blocks.push_back(overturnOrRotation(i));
shrinkBlocks.resize(blocks.size());
for (int i = 0; i < blocks.size(); i++)
{
for (auto &b : blocks[i])shrinkBlocks[i].push_back(shrink(b));
}
auto ids = foreach(blocks);
int s = 0;
for (auto &id : ids) {
if (!ok(id))continue;
s++;
cout << s << " ";
}
return 0;
}
最后
以上就是酷酷大米为你收集整理的覆盖问题的特征压缩搜索一，特征压缩搜索二，正方形骨牌覆盖问题三，覆盖问题的特征压缩搜索的全部内容，希望文章能够帮你解决覆盖问题的特征压缩搜索一，特征压缩搜索二，正方形骨牌覆盖问题三，覆盖问题的特征压缩搜索所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
![C++[POJ1849]铲雪车问题——树形DP求出树的直径代码咨询](/uploads/reation/bcimg9.png)
发表评论 取消回复