【树的直径 && 题解 && 数学推导】 POJ1849 Two

题目传送门

题目描述：

|英文|

The city consists of intersections and streets that connect them.

Heavy snow covered the city so the mayor Milan gave to the winter-service a list of streets that have to be cleaned of snow. These streets are chosen such that the number of streets is as small as possible but still every two intersections to be connected i.e. between every two intersections there will be exactly one path. The winter service consists of two snow plovers and two drivers, Mirko and Slavko, and their starting position is on one of the intersections.

The snow plover burns one liter of fuel per meter (even if it is driving through a street that has already been cleared of snow) and it has to clean all streets from the list in such order so the total fuel spent is minimal. When all the streets are cleared of snow, the snow plovers are parked on the last intersection they visited. Mirko and Slavko don’t have to finish their plowing on the same intersection.

Write a program that calculates the total amount of fuel that the snow plovers will spend.

Input
The first line of the input contains two integers: N and S, 1 <= N <= 100000, 1 <= S <= N. N is the total number of intersections; S is ordinal number of the snow plovers starting intersection. Intersections are marked with numbers 1…N.

Each of the next N-1 lines contains three integers: A, B and C, meaning that intersections A and B are directly connected by a street and that street’s length is C meters, 1 <= C <= 1000.

|中文|

这个城市由连接它们的十字路口和街道组成。
大雪覆盖了整个城市，所以米兰市长向冬季服务机构提交了一份街道必须清除积雪的清单。这些街道的选择，使街道的数量尽可能少，但仍然是每两个路口之间的连接，即每两个路口之间将有一个路径。冬季服务包括两个雪鸻和两个司机，米尔科和斯拉夫科，他们的出发点是在一个十字路口。
雪船每米燃烧1升的燃料(即使它行驶在已经清除了积雪的街道上)，它必须按照这样的顺序清理名单上的所有街道，这样燃料的总消耗量就会降到最低。当所有的街道都清除了积雪，雪鸻停在他们最后一个路口。米尔科和斯拉夫科不必在同一个十字路口完成耕作。
编写一个程序，计算雪鸻将花费的燃料总量。

Output
Write to the output the minimal amount of fuel needed to clean all streets.

Sample Input

5 2
1 2 1
2 3 2
3 4 2
4 5 1
Sample Output

6

分析：

• 假设只有一个人，且需要回到起点
  很显然，这个人想要吧所有路都走一遍，并且重新回到起点，每条路都需要走一遍返回一遍，他所花费的费用如下：
  $$2\ast \sum w[i]$$

• 假设只有一个人，且不需要返回起点
  因为不需要返回起点，所以这个人可以走完较短的路之后返回去走其它较长的路，那么较长的路就可以一下走完，但是一些分叉的较短的路仍然需要走两遍。

不理解没关系，给一个图例：

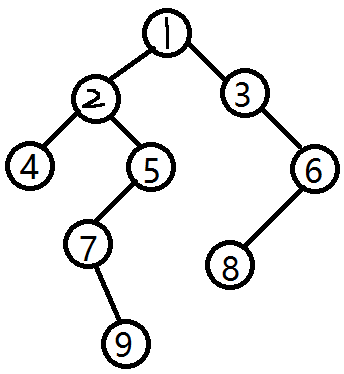
图中的最优路线是从1出发，经过1->3->6->8，然后在返回1，到2->4，在返回2，接着是5->7->9。

从图中发现，我们1->2->5->7->9的路线只走了一遍，即以起点所能到达的最远距离只走了一遍。

根据这个性质，我们推理出一下公式：
$$2\ast \sum w[i]-(从起点出发所到达的最长边)$$

• 假设有两个人，需要回到起点。
  这个就如第一个假设一样，直接得到公式：$$2\ast \sum w[i]$$

• 假设有两个人，不需要回到起点。
  这个和第二个假设类似，只是多了一个人帮他分担，在图中第二个人1->6->6->8这条路径只经过了一次。即9->7->5->2->1->3->6->8只经过了一次。这是我们突然发现这条边似乎 就是直径？大胆猜测，简单证明，得到以下公式：
  $$2\ast \sum w[i]-(树的直径)$$

那么题目就变成了一个裸题，累加所有边的边权，减掉这个树的直径即可。

那么具体代码如下：

#include<cstdio>
#include<cstring>
#include<string>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<map>
#include<queue>
using namespace std;
#define mp make_pair
typedef pair < int , int > pii;
int ans=0;
int linkk[1000001];
int len=0;
struct node{
    int y,Next,v;
}e[1000001];
int n,m,num;
int dis[1000001];
bool vis[1000001];
void bfs(int st){
	priority_queue < pii , vector < pii > , less < pii > > q;
    memset(dis,0,sizeof(dis));
    memset(vis,0,sizeof(vis));
    q.push(mp(dis[st],st));
    while (!q.empty()){
	    int x=q.top().second,vv=q.top().first;q.pop();
	    if (vis[x]) continue;
	    vis[x]=1;
	    for (int i=linkk[x];i;i=e[i].Next)
	      if (dis[e[i].y]<vv+e[i].v&&!vis[e[i].y]) dis[e[i].y]=vv+e[i].v,q.push(mp(dis[e[i].y],e[i].y));
	}
	int sum=0;
	for (int i=1;i<=n;i++)
	  if (sum<dis[i]) sum=dis[i],num=i;
}
void insert(int x,int y,int z){
    e[++len].Next=linkk[x];
    linkk[x]=len;
    e[len].y=y;
    e[len].v=z;
}
int main(){
    scanf("%d %d",&n,&m);
    for (int i=1,x,y,z;i<n;i++) scanf("%d %d %d",&x,&y,&z),insert(x,y,z),insert(y,x,z),ans+=z;
    bfs(1);bfs(num);
    printf("%d",ans*2-dis[num]);
    return 0;
}

最后

以上就是无奈羊为你收集整理的【树的直径 && 题解 && 数学推导】 POJ1849 Two的全部内容，希望文章能够帮你解决【树的直径 && 题解 && 数学推导】 POJ1849 Two所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。