1. 摘要

最近知识图（KG）的激增和实体之间以缺失关系（链接）形式存在的不完整或部分信息，推动了对知识库完成（也称为关系预测）的大量研究。最近的几项工作表明，基于卷积神经网络（CNN） 的模型能生成更丰富和更具表现力的特征嵌入，因此在关系预测方面也表现良好。
然而，我们观察到，翻译模型和基于CNN的模型都独立地处理三元组，因此无法覆盖三元组周围的局部邻域中固有的复杂和隐藏信息。为此，我们提出了一种新的基于注意力的特征嵌入方法，它可以捕获任意给定实体邻域中的实体和关系特征。此外，我们还在模型中封装了关系簇和多跳关系。我们的实证研究为我们基于注意力的模型的有效性提供了见解，我们在所有数据集上显示了与最先进的方法相比显著的性能提升。

2. 相关工作

最近，已经提出了KG嵌入的几种变体用于关系预测。这些方法可大致分为：

• 组合模型
  RESCAL、NTN和全息嵌入模型（HOLE） 是基于组成的模型的例子。RESCAL和NTN都使用张量积来捕捉丰富的相互作用，但需要大量参数来建模关系，因此计算起来很麻烦。为了克服这些缺点，HOLE使用实体嵌入的循环相关性创建了更高效和可伸缩的组合表示。
• 平移模型
  相比之下，翻译模型如TransE、DISTMULT和ComplEx是针对该问题更简单的模型。TransE考虑头部和尾部实体之间的转换操作。DISTMULT使用双线性对角模型学习嵌入，这是NTN和TransE中使用的双线性目标的特例。DISTMULT使用加权元素点乘来建模实体关系。ComplEx通过使用复数嵌入和厄米点积来推广DISTMULT。这些平移模型速度更快，需要的参数更少，训练相对更容易，但会导致KG嵌入的表达能力较低。
• 基于CNN的模型
  最近，提出了两种基于CNN的关系预测模型，即ConvE和ConvKB。ConvE使用嵌入上的二维卷积来预测链接。它包括用于最终预测的卷积层、完全连接的投影层和内积层。使用多个过滤器生成不同的特征映射以提取全局关系。这些特征映射的串联表示输入三元组。这些模型是参数有效的，但独立考虑每个三元组，而不考虑三元组之间的关系。
• 基于图形的模型
  基于图的神经网络模型称为R-GCN，是将图卷积网络（GCN）应用于关系数据的扩展。它对每个实体的邻域应用卷积运算，并为它们分配相等的权重。这种基于图形的模型并不优于基于CNN的模型。现有方法要么通过仅关注实体特征，要么通过以不相交的方式考虑实体和关系的特征来学习KG嵌入。相反，我们提出的图注意力模型整体捕获了KG中任何给定实体的n跳邻域中的多跳和语义相似关系。

3. 采用的方法

主要思想：

1. 捕获围绕给定节点的多跳关系
2. 封装实体在各种关系中扮演的角色的多样性
3. 巩固语义相似关系集群中的现有知识

我们的模型通过为邻域中的节点分配不同的权重（注意力），并通过迭代方式通过层传播注意力来实现这些目标。然而，随着模型深度的增加，远处实体的贡献呈指数下降。为了解决这个问题，我们使用（Lin等人，2015年）提出的关系组合，在n跳邻居之间引入辅助边，这样可以方便地允许实体之间的知识流动，我们的架构是编码器-解码器模型，其中我们的广义图注意力模型和ConvKB分别扮演编码器和解码器的角色。此外，该方法可以扩展到学习文本蕴涵图的有效嵌入，其中全局学习在过去已被证明是有效的，如（Berant等人，2015）和（Berant等，2010）。

3.1 Graph Attention Networks (GATs)

图卷积网络（GCN）从实体的邻域收集信息，所有邻域在信息传递中的贡献相等。为了解决GCN的缺点，图形注意力网络（GATs）学习给节点邻域中每个节点分配的不同重要性级别，而不是像在GCN中那样以同等重要性对待所有相邻节点。
图层节点的输入特征集为：
x = { x 1 ⃗ , x 2 ⃗ , . . . ， x N ⃗ } x = {vec{x_1},vec{x_2}, ...，vec{x_N}} x={x1​ ​,x2​ ​,...，xN​ ​}图层生成的经过变换节点特征向量集为：
x ′ = { x 1 ′ ⃗ , x 2 ′ ⃗ , . . . ， x N ′ ⃗ } x' = {vec{x_1'},vec{x_2'}, ...，vec{x_N'}} x′={x1′​ ​,x2′​ ​,...，xN′​ ​}
其中，$\overrightarrow{x_1}$和$\overrightarrow{x_1^{\prime }}$是实体$e_i$的输入和输出嵌入，$N$是实体的数量，单个GAT层可被表示如下：
$$e_{ij}=a(W\overrightarrow{x_i},W\overrightarrow{x_j})\text{\hspace{1em}(1)}$$
其中，$e_{ij}$是图$G$边$(e_i,e_j)$的注意力值，W是将输入特征映射到高维输出特征空间的参数化线性变换矩阵，$a$是我们选择的任何注意力函数。
每个边的注意值是源节点$e_i$的边$（e_i，e_j）$特征的重要性。这里，相对注意力${\alpha }_{ij}$使用softmax函数计算邻域中的所有值。等式 2 显示了层的输出，GAT采用多头注意力来稳定学习过程:
$$\overrightarrow{x_i^{\prime }}=\sigma (\sum _{j\in N_i}{\alpha }_{ij}W\overrightarrow{x_j})\text{\hspace{1em}(2)}$$
连接K个注意头的多头注意过程如下式 3 所示:
$$\overrightarrow{x_i^{\prime }}=|{|}_{k=1}^K\sigma (\sum _{j\in N_i}{\alpha }_{ij}W\overrightarrow{x_j})\text{\hspace{1em}(3)}$$
其中，|| 代表将多个输出连接起来，$\sigma$代表任何非线性函数，${\alpha }_{ij}^k$是由第k个注意机制计算的边的归一化注意系数，$W^k$表示第k个注意机制的对应线性变换矩阵。我们使用平均而不是级联操作来计算最终层中的输出嵌入，以实现多头注意，如以下等式4所示：
$$\overrightarrow{x_i^{\prime }}=\sigma (\frac{1}{K}\sum _{k=1}^K\sum _{j\in N_i}{\alpha }_{ij}W\overrightarrow{x_j})\text{\hspace{1em}(4)}$$

3.2 关系特征

尽管上述GATs取得了成功，但它们不适用于KGs，因为它们忽略了关系（边缘）特征,，它们是KGs的组成部分。在KG中，实体根据关联关系扮演不同角色。为此，我们提出了一种新的嵌入方法，将关系和相邻节点特征结合到注意机制中。
我们定义了一个单一的注意力层，这是我们模型的构建块。与GATs类似，我们的框架对注意力机制的特定选择是不可知的。
我们模型中的每一层都将两个嵌入矩阵作为输入。实体嵌入由矩阵$H\in R^{N_e\times T}$表示，其中第i行是实体$e_i$的嵌入，$N_e$是实体总数，T是每个实体嵌入的特征维数。通过类似的构造，关系嵌入由矩阵$G\in R^{N_r\times P}$表示，然后该层输出相应的嵌入矩阵，$H^{\prime }\in R^{N_e\times T^{\prime }}$，$G^{\prime }\in R^{N_r\times P^{\prime }}$
为了获得实体$e_i$的新嵌入，我们要学习与$e_i$相关联的每个三元组的表示。我们通过对对应于特定三元组$t_{ij}^k=（e_i，r_k，e_j）$的实体和关系特征向量的串联 执行线性变换来学习这些嵌入，如等式5所示：
$$\overrightarrow{c_{ijk}}=W_1[\overrightarrow{h_i}||\overrightarrow{h_j}||\overrightarrow{g_k}]\text{\hspace{1em}(5)}$$
其中，$\overrightarrow{c_{ijk}}$是三元组$t_{ij}^k$的向量表示，$\overrightarrow{h_i},\overrightarrow{h_j}和\overrightarrow{g_k}$ 是实体$e_i,e_j$和关系$r_k$的嵌入向量，我们学习用$\overrightarrow{b_{ijk}}$表示的三元组$t_{ij}^k$的重要性，我们执行由权重矩阵$W_2$参数化的线性变换，然后应用LeakyRelu的非线性获得三元组的绝对注意值（等式6）：
$$\overrightarrow{b_{ijk}}=LeakyReLU(W_2\overrightarrow{c_{ijk}})\text{\hspace{1em}(6)}$$
为了获得相对注意力值，将softmax应用于$\overrightarrow{b_{ijk}}$，如等式7所示:
$$\overrightarrow{a_{ijk}}=softma{x}_{jk}(\overrightarrow{b_{ijk}})\text{\hspace{1em}(7)}$$
单个三元组的相对注意力值$\overrightarrow{a_{ijk}}$的计算如下图所示

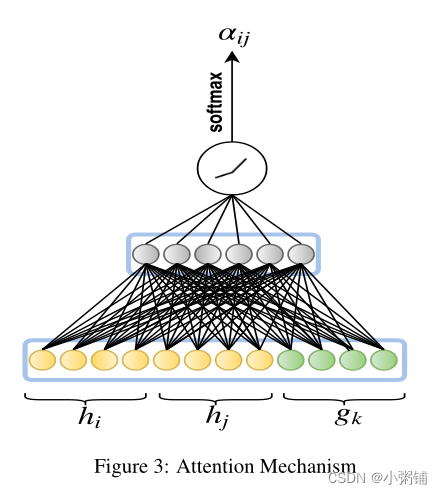
实体的新嵌入是由其关注值加权的每个三元组表示的和，如等式8所示：
$$\overrightarrow{h_i^{\prime }}=\sigma (\sum _{j\in N_i}\sum _{k\in R_{ij}}{\alpha }_{ijk}\overrightarrow{c_{ijk}})\text{\hspace{1em}(8)}$$
多头注意力用于稳定学习过程并封装更多关于邻域的信息。本质上，即为M个独立的注意力机制分别计算嵌入，然后将嵌入连接起来，得到以下表示：
$$\overrightarrow{h_i^{\prime }}=|{|}_{m=1}^M\sigma (\sum _{j\in N_i}{\alpha }_{ijk}\overrightarrow{c_{ijk}})\text{\hspace{1em}(9)}$$

我们对输入关系嵌入矩阵G执行线性变换，由权重矩阵$W^R\in R^{T\times T^{\prime }}$参数化，其中$T^{\prime }$是输出关系嵌入的维数（等式10）：
$$G^{\prime }=G\cdot W^R$$
同样，在我们模型的最后一层，我们使用平均来获得实体的最终嵌入向量（等式11）：
$$\overrightarrow{h_i^{\prime }}=\sigma (\frac{1}{M}\sum _{m=1}^M\sum _{j\in N_i}\sum _{k\in R_{ij}}{\alpha }_{ijk}\overrightarrow{c_{ijk}})\text{\hspace{1em}(11)}$$
然而，当学习新的嵌入时，实体会丢失其初始嵌入信息。为了解决这个问题，我们使用权重矩阵$W^E\in R^{T^i\times T^f}$线性变换$H^i$以获得$H^t$，其中$H^i$表示模型的输入实体嵌入，$H^t$表示转换实体嵌入，$T^i$表示初始实体嵌入的维数，$T^f$表示最终实体嵌入的维度。我们将该初始实体嵌入信息添加到从最终注意层$H^f\in R^{N_e\times T^f}$获得的实体嵌入中，如等式12所示：
$$H^{\prime \prime }=W^E{H}^t+H^f\text{\hspace{1em}(12)}$$
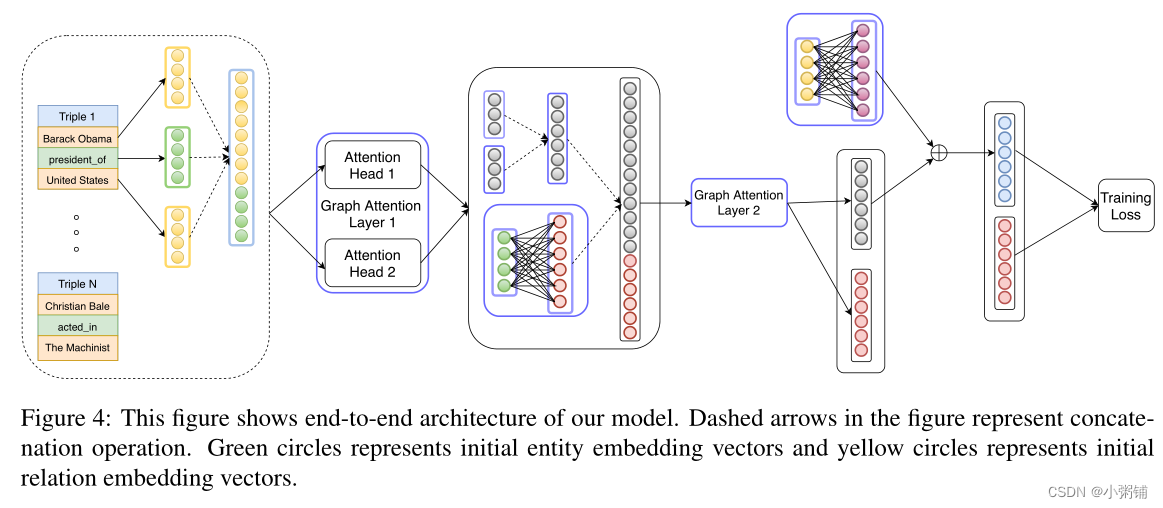
在我们的架构中，我们通过为两个实体之间的n跳邻居引入辅助关系，将边的概念扩展到有向路径。该辅助关系的嵌入是路径中所有关系嵌入的总和。我们的模型以迭代的方式积累来自实体的遥远邻居的知识。如图2所示，在模型的第一层中，所有实体都从其直接流入的邻居捕获信息。

在第二层，U.S从实体Barack Obama，Ethan Horvath，Chevrolet和Washington D.C.收集信息，这些实体已经拥有了前一层中有关其邻居Michelle Obama和Samuel L.Jackson的信息。通常，对于n层模型，输入信息在n跳邻域上累积。
图2还显示了学习新实体嵌入的聚合过程以及在n跳邻居之间引入辅助边。我们在每个广义GAT层之后和第一层之前，对每个主迭代，对实体嵌入进行归一化。

3.3 Training Objective

我们的模型借鉴了平移评分函数的思想，该函数学习嵌入，使得对于给定的有效三元组$t_{ij}^k=（e_i，r_k，e_j）$，$\overrightarrow{h_i}+\overrightarrow{g_k}\approx \overrightarrow{h_j}$条件成立，即$e_j$是通过关系$r_k$连接的$e_i$的最近邻居。具体而言，我们尝试学习实体和关系嵌入，以最小化$d_{t_{ij}}=||\overrightarrow{h_i}+\overrightarrow{g_k}-\overrightarrow{h_j}||$给出的L1范数不相似性度量。
我们使用铰链损失（hinge-loss)训练我们的模型：
L ( Ω ) = ∑ t i j ∈ S ∑ t i j ′ ∈ S ′ m a x { d t i j ′ − d t i j + γ , 0 } L(Omega) = sum_{t_{ij} in S} sum_{t_{ij}' in S'} max{d_{t_{ij}'} - d_{t_{ij}} + gamma, 0} L(Ω)=tij​∈S∑​tij′​∈S′∑​max{dtij′​​−dtij​​+γ,0}
其中，$\gamma >0$是margin hyper-parameter，$S$是有效的三元组集，$S^{\prime }$是无效的三元组集，形式如下:

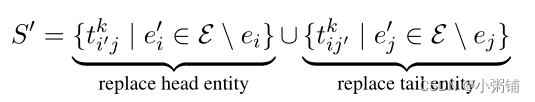
3.4 Decoder

我们的模型使用ConvKB作为解码器。卷积层的目的是分析三元组$t_{ij}^k$在每个维度上的全局嵌入特性，并推广我们模型中的过渡特性。具有多个特征映射的得分函数表示如下：
$$f(t_{ij}^k)=(|{|}_{m=1}^{\Omega }ReLU([\overrightarrow{h_i}||\overrightarrow{h_j}||\overrightarrow{g_k}]\ast {\omega }^m)$$
其中，${\omega }^m$是第m层卷积过滤器，$\Omega$是表示所使用的滤波器数量的超参数，*是卷积算子，并且$W\in R^{{\Omega }_k\times 1}$是用于计算三元组的最终分数的线性变换矩阵，模型使用soft-margin loss进行训练：
L = ∑ t i j k ∈ { S ∪ S ′ } l o g ( 1 + e x p ( l t i j k ⋅ f ( t i j k ) + λ 2 ∣ ∣ W ∣ ∣ 2 2 ) L = sum_{t^k_{ij} in { Scup S' }} log(1+exp(l_{t^k_{ij} cdot f(t^k_{ij})} + frac{lambda}{2}||W||^2_2) L=tijk​∈{S∪S′}∑​log(1+exp(ltijk​⋅f(tijk​)​+2λ​∣∣W∣∣22​)
其中 $$l_{t_{ij}^k}=\{\begin{array}{rlr}1，& for& t_{ij}^k\in S\\ -1，& for& t_{ij}^k\in S^{\prime }\end{array}$$

4. 创新点

• 第一个专门针对KG上的关系预测的基于图注意力的嵌入模型
• 我们推广和扩展了图注意机制（GATs），以捕获给定实体的多跳邻域中的实体和关系特征。
• 我们的实验结果表明，与最先进的关系预测方法相比，有了明显和实质性的改进

5. 未来工作

在实验中可以看出，WN18RR数据集的高度稀疏和分层结构对我们的方法提出了挑战，因为该方法不能以自上而下的递归方式捕获信息。未来我们可以扩展该方法，以更好地处理分层图，并在我们的图注意力模型中捕捉实体（如主题）之间的高阶关系。

最后

以上就是优秀小兔子为你收集整理的论文阅读：Learning Attention-based Embeddings for Relation Prediction in Knowledge Graphs1. 摘要2. 相关工作3. 采用的方法4. 创新点5. 未来工作的全部内容，希望文章能够帮你解决论文阅读：Learning Attention-based Embeddings for Relation Prediction in Knowledge Graphs1. 摘要2. 相关工作3. 采用的方法4. 创新点5. 未来工作所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。