残差Jacobian的推导

视觉重投影残差的Jacobian

视觉残差为：

对于第i帧中的特征点，它投影到第j帧相机坐标系下的值为：

拆成三维坐标形式为：

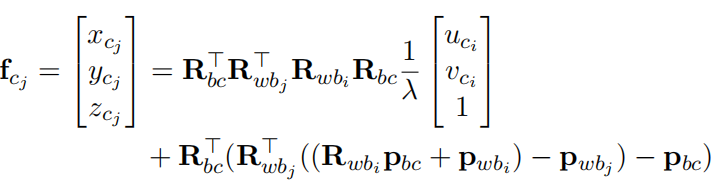
将齐次坐标拆为R（旋转）和P（位姿）

为了简化公式，先定义如下变量：

Jacobian为视觉误差对两个时刻的状态量，外参以及逆深度求导：

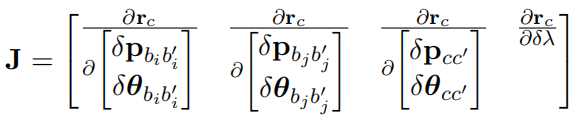
根据链式法则，Jacobian的计算可以分成两步走，第一步误差对求导

rc的每一列 对 fcj的每一行进行求导，得到2X3矩阵

第二步对对各状态量求导：

1. 对i时刻的状态量求导

a.对i时刻位移求导，可直接写出如下：

b.对i时刻角度增量求导

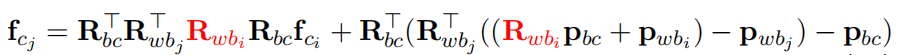
上面公式和i时刻角度相关的量并不多，下面为了简化，直接丢弃了不相关的部分

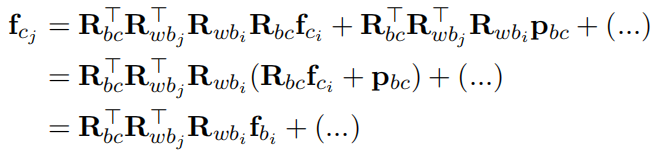
Jacobian为

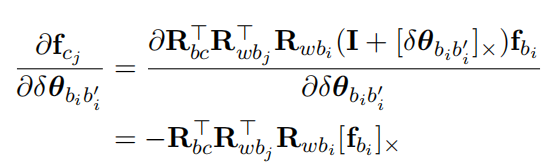
2.对j时刻的状态量求导

a. 对位移求导：

b.对角度增量求导，同上面的操作，也简化一下公式

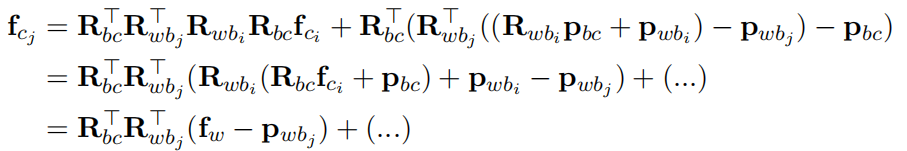
Jacobian为：

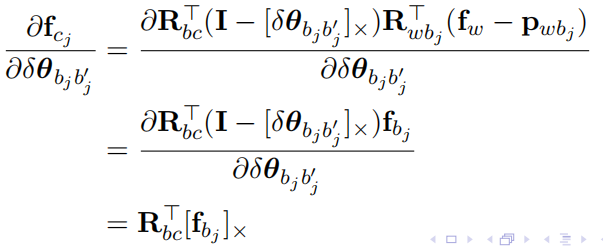
3. 对imu和相机之间的外参求导

a.对位移求导：

b. 对角度增量求导，由于fcj都和Rbc有关，并且比较复杂，所以这次分两部分求导

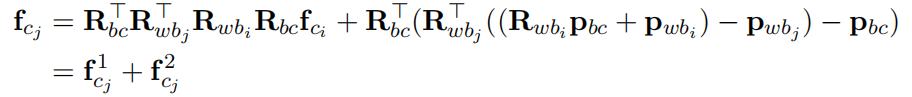
第一部分Jacobian为

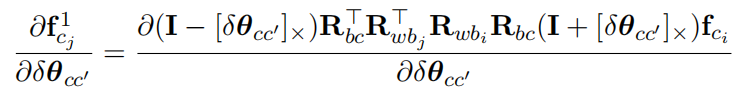
分子可写成：

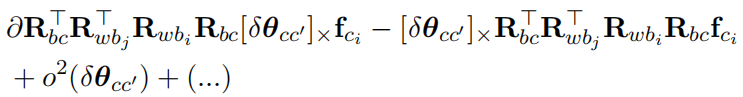
所以可以得到：

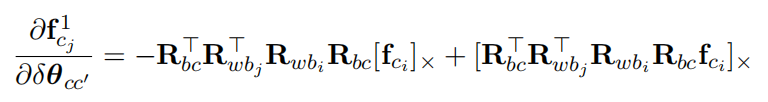
第二部分Jacobian为

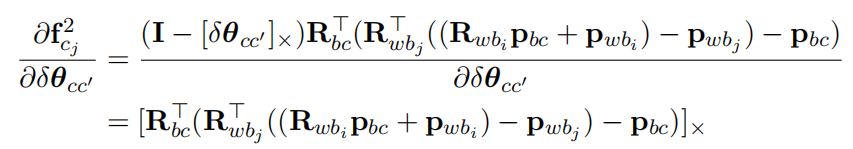
4.视觉误差对特征逆深度的求导

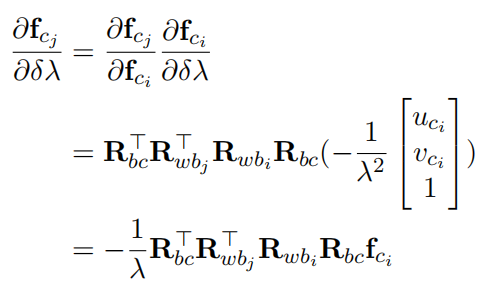
IMU预积分残差的雅克比

IMU误差相对于优化变量的Jacobian

在求解非线性方程时，需要知道误差eB对两个关键帧i，j的状态量p,q,v,的Jacobian

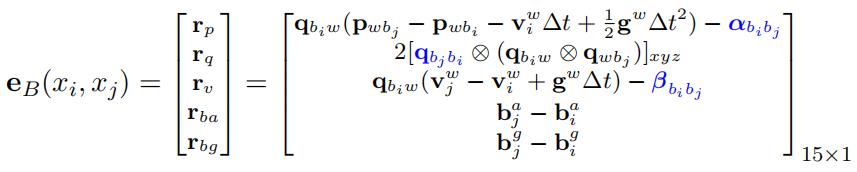
其中对i时刻的求导就显得十分复杂，下面进行详细讨论

因为i时刻的bias相关的预积分计算是通过迭代一步一步累计递推的，可以算但是太复杂。所以对于预积分量直接在i时刻的bias附近用一阶泰勒展开来近似，而不用真的去迭代。

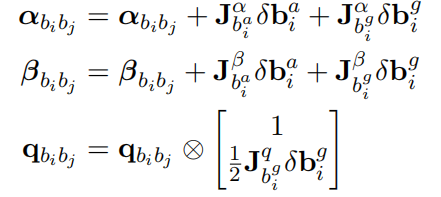
其中J表示预积分量对i时刻的bias求导，这些雅克比根据前面讨论的协方差传递公式，能一步步递推得到 

下面讨论IMU误差相对于两帧的PVQ的Jacobian：

由于的误差形式很相近，对各状态量求导的Jacobian形式也很相似，所以这里只对rv的推导进行详细介绍

（1）对i时刻位移Jacobian：

（2）对i时刻旋转Jacobian

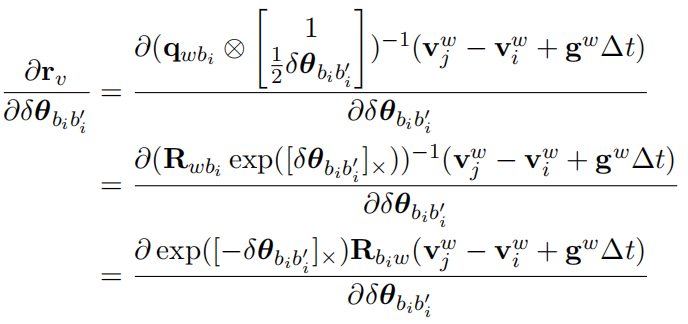
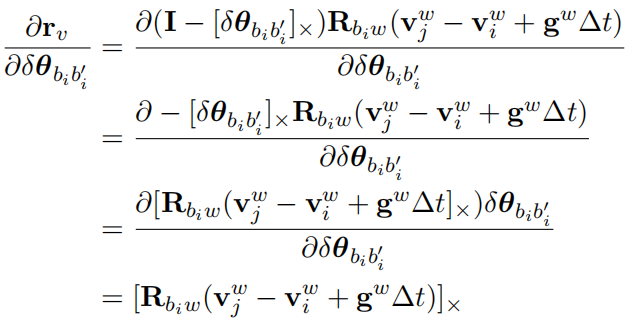
（3）对i时刻速度Jacobian：

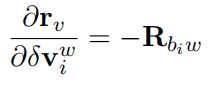
（4）对i时刻的加速度bias的Jacobian，注意bias量只和预积分β有关

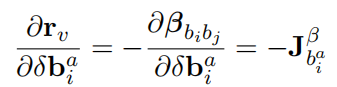
IMU角度误差相对优化变量的Jacobian

（1）对i时刻姿态求导

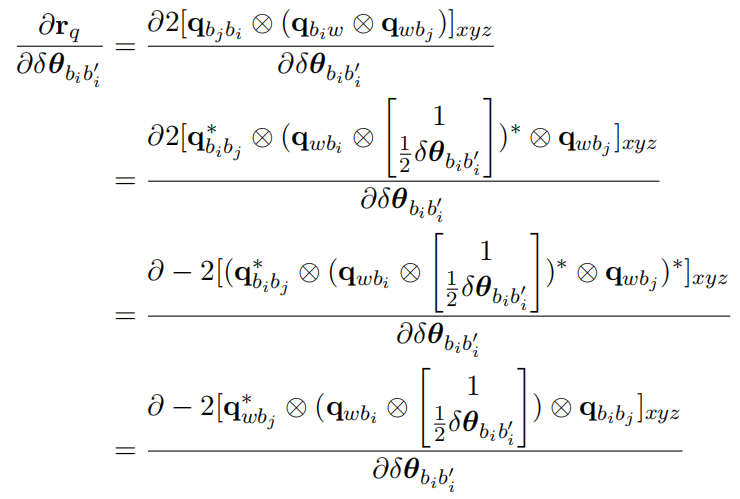
上式可化简为：

（2）角度误差对j时刻姿态求导

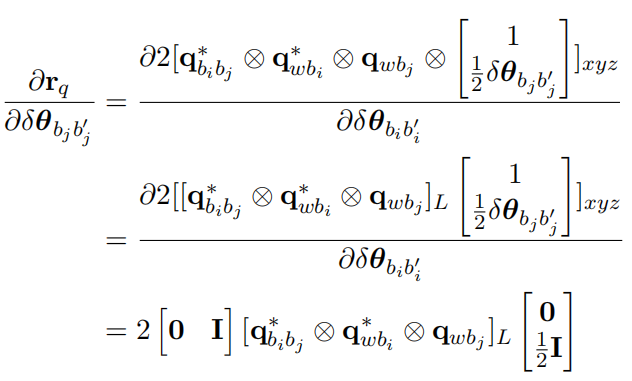
（3）角度误差对i时刻陀螺仪偏置

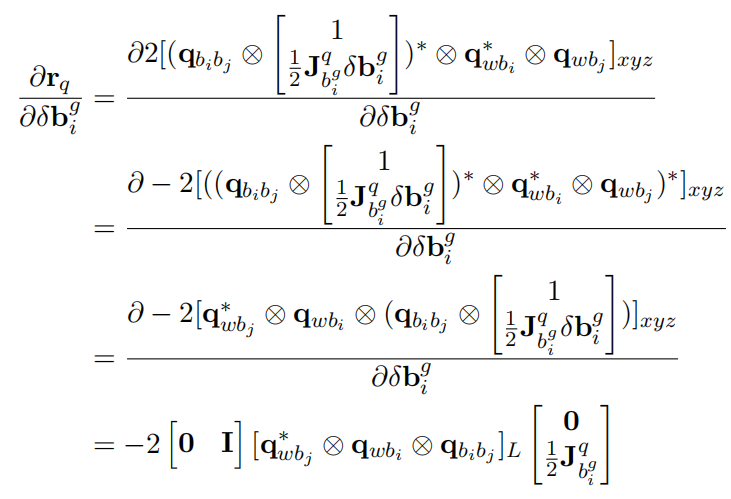
最后

以上就是羞涩跳跳糖为你收集整理的残差Jacobian的推导—手写VIO课程笔记3残差Jacobian的推导的全部内容，希望文章能够帮你解决残差Jacobian的推导—手写VIO课程笔记3残差Jacobian的推导所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。