初步认识g2o的边

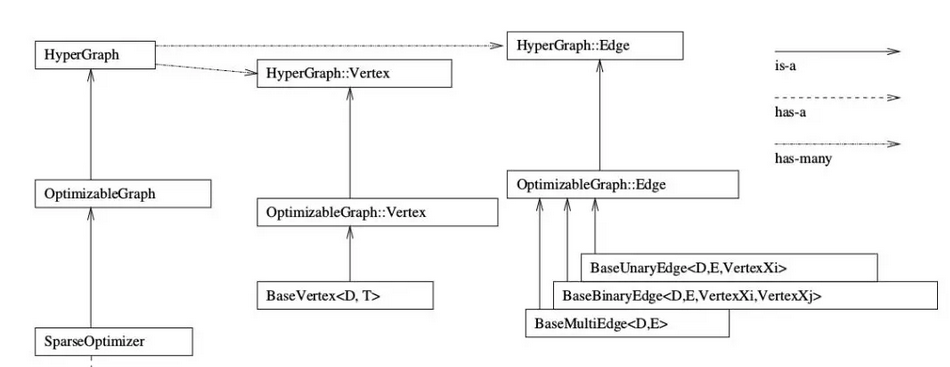边的继承关系上图所示，对应的文件为：

• g2o/g2o/core/hyper_graph.h
• g2o/g2o/core/optimizable_graph.h
• g2o/g2o/core/base_edge.h

BaseUnaryEdge，BaseBinaryE加粗样式dge，BaseMultiEdge 分别表示一元边，两元边，多元边。
一元边你可以理解为一条边只连接一个顶点，两元边理解为一条边连接两个顶点，也就是我们常见的边啦，多元边理解为一条边可以连接多个（3个以上）顶点

参数
主要就是 几个参数：D, E, VertexXi, VertexXj，他们的分别代表：

• D 是 int 型，表示测量值的维度 （dimension）
• E 表示测量值的数据类型
• VertexXi，VertexXj 分别表示不同顶点的类型

比如我们用边表示三维点投影到图像平面的重投影误差，就可以设置输入参数如下：

BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>

二元边。第1个2是说测量值是2维的，也就是图像像素坐标x,y的差值，对应测量值的类型是Vector2D，两个顶点也就是优化变量分别是空间点位置 VertexSBAPointXYZ，和李代数位姿VertexSE3Expmap

除了输入参数外，定义边我们通常需要复写一些重要的成员函数，顶点里主要复写了顶点更新函数oplusImpl和顶点重置函数setToOriginImpl

成员函数

virtual bool read(std::istream& is);
virtual bool write(std::ostream& os) const;
virtual void computeError();
virtual void linearizeOplus();

• read，write：分别是读盘、存盘函数，一般情况下不需要进行读/写操作的话，仅仅声明一下就可以
• computeError函数：非常重要，是使用当前顶点的值计算的测量值与真实的测量值之间的误差
• linearizeOplus函数：非常重要，是在当前顶点的值下，该误差对优化变量的偏导数，也就是我们说的Jacobian

除了上面几个成员函数，还有几个重要的成员变量和函数也一并解释一下：

_measurement：存储观测值
_error：存储computeError() 函数计算的误差
_vertices[]：存储顶点信息，比如二元边的话，_vertices[] 的大小为2，存储顺序和调用setVertex(int, vertex) 是设定的int 有关（0 或1）
setId(int)：来定义边的编号（决定了在H矩阵中的位置）
setMeasurement(type) 函数来定义观测值
setVertex(int, vertex) 来定义顶点
setInformation() 来定义协方差矩阵的逆

定义g2o的边

模板如下，基本上定义g2o中的边，就是如下套路：

 class myEdge: public g2o::BaseBinaryEdge<errorDim, errorType, Vertex1Type, Vertex2Type>
  {
      public:
      EIGEN_MAKE_ALIGNED_OPERATOR_NEW      
      myEdge(){}     
      virtual bool read(istream& in) {}
      virtual bool write(ostream& out) const {}      
      virtual void computeError() override
      {
          // ...
          _error = _measurement - Something;
      }      
      virtual void linearizeOplus() override
      {
          _jacobianOplusXi(pos, pos) = something;
          // ...         
          /*
          _jocobianOplusXj(pos, pos) = something;
          ...
          */
      }      
      private:
      // data
  }

最重要的就是computeError()，linearizeOplus()两个函数了

eg1:
一元边，主要是定义误差函数

// 误差模型 模板参数：观测值维度，类型，连接顶点类型
class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    CurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}
    // 计算曲线模型误差
    void computeError()
    {
        const CurveFittingVertex* v = static_cast<const CurveFittingVertex*> (_vertices[0]);
        const Eigen::Vector3d abc = v->estimate();
        _error(0,0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) ) ;
    }
    virtual bool read( istream& in ) {}
    virtual bool write( ostream& out ) const {}
public:
    double _x;  // x 值， y 值为 _measurement
};

eg2:
二元边：3D-2D点的PnP 问题，也就是最小化重投影误差问题，。地址：g2o/types/sba/types_six_dof_expmap.h

//继承了BaseBinaryEdge类，观测值是2维，类型Vector2D,顶点分别是三维点、李群位姿
class G2O_TYPES_SBA_API EdgeProjectXYZ2UV : public  BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>{
  public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
    //1. 默认初始化
    EdgeProjectXYZ2UV();
    //2. 计算误差
    void computeError()  {
      //李群相机位姿v1
      const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[1]);
      // 顶点v2
      const VertexSBAPointXYZ* v2 = static_cast<const VertexSBAPointXYZ*>(_vertices[0]);
      //相机参数
      const CameraParameters * cam
        = static_cast<const CameraParameters *>(parameter(0));
     //误差计算，测量值减去估计值，也就是重投影误差obs-cam
     //估计值计算方法是T*p,得到相机坐标系下坐标，然后在利用camera2pixel()函数得到像素坐标。
      Vector2D obs(_measurement);
      _error = obs-cam->cam_map(v1->estimate().map(v2->estimate()));
    }
    //3. 线性增量函数，也就是雅克比矩阵J的计算方法
    virtual void linearizeOplus();
    //4. 相机参数
    CameraParameters * _cam; 
    bool read(std::istream& is);
    bool write(std::ostream& os) const;
};

cam_map 函数功能是把相机坐标系下三维点（输入）用内参转换为图像坐标（输出），函数在g2o/types/sba/types_six_dof_expmap.cpp，具体代码如下所示:

Vector2  CameraParameters::cam_map(const Vector3 & trans_xyz) const {
  Vector2 proj = project2d(trans_xyz);
  Vector2 res;
  res[0] = proj[0]*focal_length + principle_point[0];
  res[1] = proj[1]*focal_length + principle_point[1];
  return res;
}

.map函数，它的功能是把世界坐标系下三维点变换到相机坐标系，函数在g2o/types/sim3/sim3.h

      Vector3 map (const Vector3& xyz) const {
        return s*(r*xyz) + t;
      }

观测相机方程关于相机位姿与特征点的两个导数矩阵


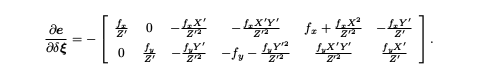
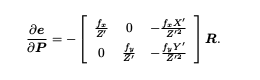
EdgeProjectXYZ2UV 的 linearizeOplus 函数

void EdgeProjectXYZ2UV::linearizeOplus() {
  VertexSE3Expmap * vj = static_cast<VertexSE3Expmap *>(_vertices[1]);
  SE3Quat T(vj->estimate());
  VertexSBAPointXYZ* vi = static_cast<VertexSBAPointXYZ*>(_vertices[0]);
  Vector3D xyz = vi->estimate();
  Vector3D xyz_trans = T.map(xyz);

  double x = xyz_trans[0];
  double y = xyz_trans[1];
  double z = xyz_trans[2];
  double z_2 = z*z;

  const CameraParameters * cam = static_cast<const CameraParameters *>(parameter(0));

  Matrix<double,2,3,Eigen::ColMajor> tmp;
  tmp(0,0) = cam->focal_length;
  tmp(0,1) = 0;
  tmp(0,2) = -x/z*cam->focal_length;

  tmp(1,0) = 0;
  tmp(1,1) = cam->focal_length;
  tmp(1,2) = -y/z*cam->focal_length;

  _jacobianOplusXi =  -1./z * tmp * T.rotation().toRotationMatrix();

  _jacobianOplusXj(0,0) =  x*y/z_2 *cam->focal_length;
  _jacobianOplusXj(0,1) = -(1+(x*x/z_2)) *cam->focal_length;
  _jacobianOplusXj(0,2) = y/z *cam->focal_length;
  _jacobianOplusXj(0,3) = -1./z *cam->focal_length;
  _jacobianOplusXj(0,4) = 0;
  _jacobianOplusXj(0,5) = x/z_2 *cam->focal_length;

  _jacobianOplusXj(1,0) = (1+y*y/z_2) *cam->focal_length;
  _jacobianOplusXj(1,1) = -x*y/z_2 *cam->focal_length;
  _jacobianOplusXj(1,2) = -x/z *cam->focal_length;
  _jacobianOplusXj(1,3) = 0;
  _jacobianOplusXj(1,4) = -1./z *cam->focal_length;
  _jacobianOplusXj(1,5) = y/z_2 *cam->focal_length;
}

向图中添加边

eg1:
曲线拟合的例子

    // 往图中增加边
    for ( int i=0; i<N; i++ )
    {
        CurveFittingEdge* edge = new CurveFittingEdge( x_data[i] );
        edge->setId(i);
        edge->setVertex( 0, v );                // 设置连接的顶点
        edge->setMeasurement( y_data[i] );      // 观测数值
        edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵：协方差矩阵之逆
        optimizer.addEdge( edge );
    }

eg2:
slambook/ch7/pose_estimation_3d2d.cpp

    index = 1;
    for ( const Point2f p:points_2d )
    {
        g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();
        edge->setId ( index );
        edge->setVertex ( 0, dynamic_cast<g2o::VertexSBAPointXYZ*> ( optimizer.vertex ( index ) ) );
        edge->setVertex ( 1, pose );
        edge->setMeasurement ( Eigen::Vector2d ( p.x, p.y ) );
        edge->setParameterId ( 0,0 );
        edge->setInformation ( Eigen::Matrix2d::Identity() );
        optimizer.addEdge ( edge );
        index++;
    }

setVertex 定义顶点，有两个

• 一个是 0 和 VertexSBAPointXYZ 类型的顶点
• 一个是1 和pose

setVertex在g2o官网的定义：

// set the ith vertex on the hyper-edge to the pointer supplied
void setVertex(size_t i, Vertex* v) { assert(i < _vertices.size() && "index out of bounds"); _vertices[i]=v;}

_vertices[i] 里的i就是我们这里的0和1，再看看这里边的类型： g2o::EdgeProjectXYZ2UV
的定义

class G2O_TYPES_SBA_API EdgeProjectXYZ2UV 
.....
 //李群相机位姿v1
const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[1]);
// 顶点v2
const VertexSBAPointXYZ* v2 = static_cast<const VertexSBAPointXYZ*>(_vertices[0]);

_vertices[0] 对应的是 VertexSBAPointXYZ 类型的顶点，也就是三维点，_vertices[1] 对应的是VertexSE3Expmap 类型的顶点，也就是位姿pose。

实践.

题目：用直接法Bundle Adjustment 估计相机位姿。给定3张图片，两个txt文件

• poses.txt中存储3张图片对应的相机初始位姿（Tcw），格式为：timestamp, tx, ty, tz, qx, qy, qz, qw ，分别对应时间戳、平移、旋转（四元数）-
• points.txt中存储的是3D点集合以及该点周围 4x4 窗口的灰度值，记做 I§i，格式为：x, y, z, 灰度1，灰度2…，灰度16

我们把每个3D点投影到对应图像中，用投影后点周围的灰度值与原始窗口的灰度值差异作为待优化误差。

#include <iostream>

using namespace std;

#include <g2o/core/base_unary_edge.h>
#include <g2o/core/base_binary_edge.h>
#include <g2o/core/base_vertex.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/solvers/dense/linear_solver_dense.h>

#include <g2o/core/robust_kernel.h>
#include <g2o/core/robust_kernel_impl.h>
#include <g2o/types/sba/types_six_dof_expmap.h>

#include <Eigen/Core>
#include <sophus/se3.h>
#include <opencv2/opencv.hpp>

#include <pangolin/pangolin.h>
#include <boost/format.hpp>
using namespace Sophus;
using namespace pangolin;
using namespace g2o;

#define DEBUG false

typedef vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> VecSE3;
typedef vector<Eigen::Vector3d, Eigen::aligned_allocator<Eigen::Vector3d>> VecVec3d;

// global variables
string pose_file = "/home/xiaohu/learn_SLAM/zuoye18/练习18-g2o边代码框架/poses.txt";
string points_file = "/home/xiaohu/learn_SLAM/zuoye18/练习18-g2o边代码框架/points.txt";

// intrinsics
float fx = 277.34;
float fy = 291.402;
float cx = 312.234;
float cy = 239.777;

inline bool bInImage(float u, float v, int w, int h)
{
    if(u>=0 && u<w && v>=0 && v<h)
        return true;
    else
        return false;
}
// bilinear interpolation
inline float GetPixelValue(const cv::Mat &img, float x, float y) {
    uchar *data = &img.data[int(y) * img.step + int(x)];
    float xx = x - floor(x);
    float yy = y - floor(y);
    return float(
            (1 - xx) * (1 - yy) * data[0] +
            xx * (1 - yy) * data[1] +
            (1 - xx) * yy * data[img.step] +
            xx * yy * data[img.step + 1]
    );
}

// g2o vertex that use sophus::SE3 as pose
class VertexSophus : public g2o::BaseVertex<6, Sophus::SE3> {
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    VertexSophus() {}

    ~VertexSophus() {}

    bool read(std::istream &is) {}

    bool write(std::ostream &os) const {}

    virtual void setToOriginImpl() {
        _estimate = Sophus::SE3();
    }

    virtual void oplusImpl(const double *update_) {
        Eigen::Map<const Eigen::Matrix<double, 6, 1>> update(update_);
        setEstimate(Sophus::SE3::exp(update) * estimate());
    }
};

// TODO edge of projection error, implement it
// 16x1 error, which is the errors in patch
typedef Eigen::Matrix<double,16,1> Vector16d;
class EdgeDirectProjection : public g2o::BaseBinaryEdge<16, Vector16d, g2o::VertexSBAPointXYZ, VertexSophus> {
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

    EdgeDirectProjection(float *color, cv::Mat &target) {
        this->origColor = color;
        this->targetImg = target;
        this->w = targetImg.cols;
        this->h = targetImg.rows;

    }

    ~EdgeDirectProjection() {}

    virtual void computeError() override {

        // ----------------  开始你的代码 ----------------------//
		// 参考十四讲中直接法BA部分
        // 空间点
        const VertexSBAPointXYZ* vertexPw = static_cast<const VertexSBAPointXYZ* >(vertex(0));
        //李群相机位姿
        const VertexSophus* vertexTcw = static_cast<const VertexSophus* >(vertex(1));
        Vector3d Pc = vertexTcw->estimate() * vertexPw->estimate();
        float u = Pc[0]/Pc[2] * fx + cx;
        float v = Pc[1]/Pc[2] * fy + cy;
        if(!bInImage(u-3,v-3,w,h) || !bInImage(u+2,v+2,w,h)) {
            this->setLevel(1);
            for(int n=0;n<16;n++)
                _error[n] = 0;
        } else {
            for(int i = -2; i<2; i++) {
                for(int j = -2; j<2; j++) {
                    int num = 4 * i + j + 10;
                    _error[num] = origColor[num] - GetPixelValue(targetImg, u+i, v+j);
                }
            }
        }

        // ----------------  结束你的代码 ----------------------//
    }
	
	// 下面函数不用自己写了，但是要能看懂
    virtual void linearizeOplus() override
    {
        if(level()==1)
        {
            _jacobianOplusXi = Matrix<double,16,3>::Zero();
            _jacobianOplusXj = Matrix<double,16,6>::Zero();
            return;
        }
        const VertexSBAPointXYZ* vertexPw = static_cast<const VertexSBAPointXYZ* >(vertex(0));
        const VertexSophus* vertexTcw = static_cast<const VertexSophus* >(vertex(1));
        Vector3d Pc = vertexTcw->estimate() * vertexPw->estimate();
        float x = Pc[0];
        float y = Pc[1];
        float z = Pc[2];
        float inv_z = 1.0/z;
        float inv_z2 = inv_z * inv_z;
        float u = x * inv_z * fx + cx;
        float v = y * inv_z * fy + cy;

        Matrix<double,2,3> J_Puv_Pc;
        J_Puv_Pc(0,0) = fx * inv_z;
        J_Puv_Pc(0,1) = 0;
        J_Puv_Pc(0,2) = -fx * x * inv_z2;
        J_Puv_Pc(1,0) = 0;
        J_Puv_Pc(1,1) = fy * inv_z;
        J_Puv_Pc(1,2) = -fy * y * inv_z2;


        Matrix<double,3,6> J_Pc_kesi = Matrix<double,3,6>::Zero();
        J_Pc_kesi(0,0) = 1;
        J_Pc_kesi(0,4) = z;
        J_Pc_kesi(0,5) = -y;
        J_Pc_kesi(1,1) = 1;
        J_Pc_kesi(1,3) = -z;
        J_Pc_kesi(1,5) = x;
        J_Pc_kesi(2,2) = 1;
        J_Pc_kesi(2,3) = y;
        J_Pc_kesi(2,4) = -x;

        Matrix<double,1,2> J_I_Puv;
        for(int i = -2; i<2; i++)
            for(int j = -2; j<2; j++) {
                int num = 4 * i + j + 10;
                J_I_Puv(0,0) = (GetPixelValue(targetImg,u+i+1,v+j) - GetPixelValue(targetImg,u+i-1,v+j))/2;
                J_I_Puv(0,1) = (GetPixelValue(targetImg,u+i,v+j+1) - GetPixelValue(targetImg,u+i,v+j-1))/2;
                _jacobianOplusXi.block<1,3>(num,0) = -J_I_Puv * J_Puv_Pc * vertexTcw->estimate().rotation_matrix();
                _jacobianOplusXj.block<1,6>(num,0) = -J_I_Puv * J_Puv_Pc * J_Pc_kesi;
            }
    }
    virtual bool read(istream &in) {}

    virtual bool write(ostream &out) const {}

private:
    cv::Mat targetImg;  // the target image
    float *origColor = nullptr;   // 16 floats, the color of this point
    int w;
    int h;
};

// plot the poses and points for you, need pangolin
void Draw(const VecSE3 &poses, const VecVec3d &points);

int main(int argc, char **argv) {

    // read poses and points
    VecSE3 poses;
    VecVec3d points;
    ifstream fin(pose_file);

    while (!fin.eof()) {
        double timestamp = 0;
        fin >> timestamp;
        if (timestamp == 0) break;
        double data[7];
        for (auto &d: data) fin >> d;
        poses.push_back(Sophus::SE3(
                Eigen::Quaterniond(data[6], data[3], data[4], data[5]),
                Eigen::Vector3d(data[0], data[1], data[2])
        ));
        if (!fin.good()) break;
    }
    fin.close();

    vector<float *> color;
    fin.open(points_file);
    while (!fin.eof()) {
        double xyz[3] = {0};
        for (int i = 0; i < 3; i++) fin >> xyz[i];
        if (xyz[0] == 0) break;
        points.push_back(Eigen::Vector3d(xyz[0], xyz[1], xyz[2]));
        float *c = new float[16];
        for (int i = 0; i < 16; i++) fin >> c[i];
        color.push_back(c);

        if (fin.good() == false) break;
    }
    fin.close();

    cout << "poses: " << poses.size() << ", points: " << points.size() << ", color: "<<color.size()<<endl;

    // read images
    vector<cv::Mat> images;
    boost::format fmt("../%d.png");
    for (int i = 0; i < 3; i++) {
        images.push_back(cv::imread((fmt % i).str(), 0));
    }
    cout<<"images: "<<images.size()<<endl;

//    typedef g2o::BlockSolver< g2o::BlockSolverTraits<6,3> > Block;  // pose 维度为 6, landmark 维度为 3
//    // 第1步：创建一个线性求解器LinearSolver
//    Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>();
//
//    // 第2步：创建BlockSolver。并用上面定义的线性求解器初始化
//    Block* solver_ptr = new Block (  std::unique_ptr<Block::LinearSolverType>(linearSolver) );
//
//    // 第3步：创建总求解器solver。并从GN, LM, DogLeg 中选一个，再用上述块求解器BlockSolver初始化
//    g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( std::unique_ptr<Block>(solver_ptr) );
//
//    // 第4步：创建稀疏优化器
//    g2o::SparseOptimizer optimizer;
//    optimizer.setAlgorithm ( solver );

    // old g2o version
    typedef g2o::BlockSolver< g2o::BlockSolverTraits<6,3> > Block;  // pose 维度为 6, landmark 维度为 3
    Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>(); // 线性方程求解器
    Block* solver_ptr = new Block ( linearSolver );     // 矩阵块求解器
    g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( solver_ptr );
    g2o::SparseOptimizer optimizer;
    optimizer.setAlgorithm ( solver );

    // 第5步：添加顶点和边
    // ----------------  开始你的代码 ----------------------//
    for(int i = 0; i < points.size(); i++) {
        VertexSBAPointXYZ* vertexPw = new VertexSBAPointXYZ();
        vertexPw->setEstimate(points[i]);
        vertexPw->setId(i);
        vertexPw->setMarginalized(true);
        optimizer.addVertex(vertexPw);
    }

    for(int j = 0; j < poses.size(); j++) {
        VertexSophus* vertexTcw = new VertexSophus();
        vertexTcw->setEstimate(poses[j]);
        vertexTcw->setId(j + points.size());
        optimizer.addVertex(vertexTcw);
    }

    for(int c = 0; c < poses.size(); c++)
        for(int p = 0; p < points.size(); p++) {
            EdgeDirectProjection* edge = new EdgeDirectProjection(color[p],images[c]);
            edge->setVertex(0,dynamic_cast<VertexSBAPointXYZ*>(optimizer.vertex(p)));
            edge->setVertex(1,dynamic_cast<VertexSophus*>(optimizer.vertex(c + points.size())));
            edge->setInformation(Matrix<double,16,16>::Identity());
            RobustKernelHuber* rk = new RobustKernelHuber;
            rk->setDelta(1.0);
            edge->setRobustKernel(rk);
            optimizer.addEdge(edge);
        }
    // ----------------  结束你的代码 ----------------------//

    // 第6步：执行优化
    optimizer.initializeOptimization(0);
    optimizer.optimize(200);

    // 从optimizer中获取结果
    for(int c = 0; c < poses.size(); c++)
        for(int p = 0; p < points.size(); p++) {
            Vector3d Pw = dynamic_cast<VertexSBAPointXYZ*>(optimizer.vertex(p))->estimate();
            points[p] = Pw;
            SE3 Tcw = dynamic_cast<VertexSophus*>(optimizer.vertex(c + points.size()))->estimate();
            poses[c] = Tcw;
        }


    // plot the optimized points and poses
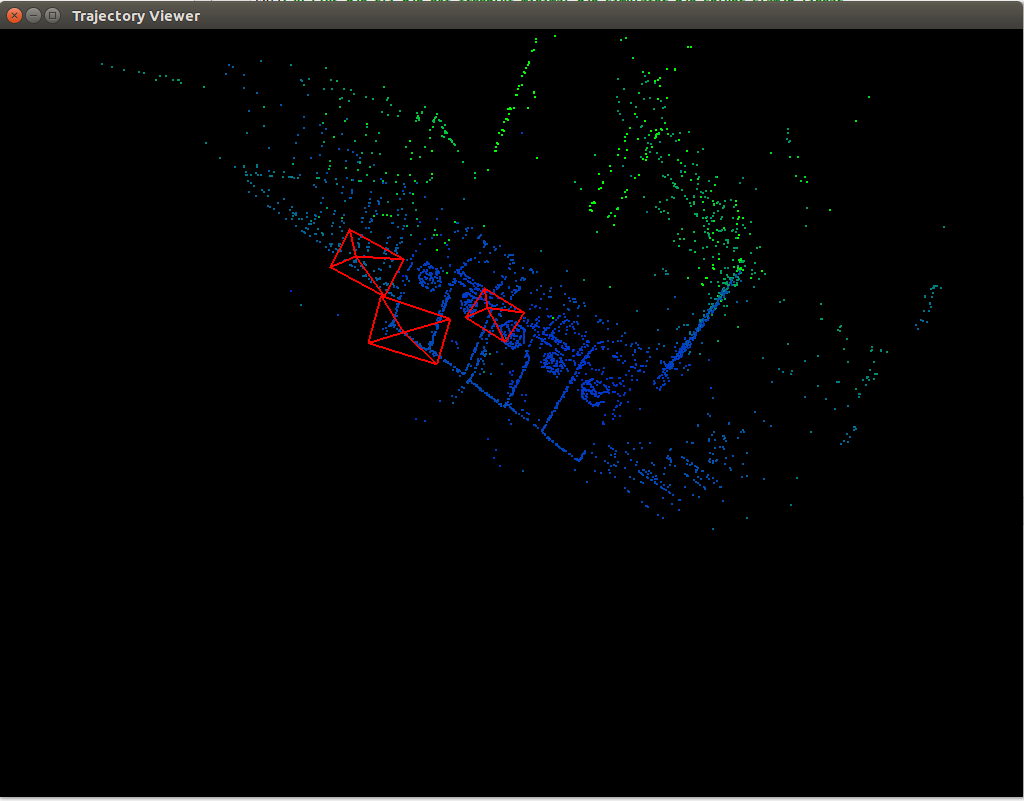
    Draw(poses, points);

    // delete color data
    for (auto &c: color) delete[] c;
    return 0;
}

// 画图函数，无需关注
void Draw(const VecSE3 &poses, const VecVec3d &points) {
    if (poses.empty() || points.empty()) {
        cerr << "parameter is empty!" << endl;
        return;
    }
    cout<<"Draw poses: "<<poses.size()<<", points: "<<points.size()<<endl;
    // create pangolin window and plot the trajectory
    pangolin::CreateWindowAndBind("Trajectory Viewer", 1024, 768);
    glEnable(GL_DEPTH_TEST);
    glEnable(GL_BLEND);
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);

    pangolin::OpenGlRenderState s_cam(
            pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
            pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
    );

    pangolin::View &d_cam = pangolin::CreateDisplay()
            .SetBounds(0.0, 1.0, pangolin::Attach::Pix(175), 1.0, -1024.0f / 768.0f)
            .SetHandler(new pangolin::Handler3D(s_cam));


    while (pangolin::ShouldQuit() == false) {
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

        d_cam.Activate(s_cam);
        glClearColor(0.0f, 0.0f, 0.0f, 0.0f);

        // draw poses
        float sz = 0.1;
        int width = 640, height = 480;
        for (auto &Tcw: poses) {
            glPushMatrix();
            Sophus::Matrix4f m = Tcw.inverse().matrix().cast<float>();
            glMultMatrixf((GLfloat *) m.data());
            glColor3f(1, 0, 0);
            glLineWidth(2);
            glBegin(GL_LINES);
            glVertex3f(0, 0, 0);
            glVertex3f(sz * (0 - cx) / fx, sz * (0 - cy) / fy, sz);
            glVertex3f(0, 0, 0);
            glVertex3f(sz * (0 - cx) / fx, sz * (height - 1 - cy) / fy, sz);
            glVertex3f(0, 0, 0);
            glVertex3f(sz * (width - 1 - cx) / fx, sz * (height - 1 - cy) / fy, sz);
            glVertex3f(0, 0, 0);
            glVertex3f(sz * (width - 1 - cx) / fx, sz * (0 - cy) / fy, sz);
            glVertex3f(sz * (width - 1 - cx) / fx, sz * (0 - cy) / fy, sz);
            glVertex3f(sz * (width - 1 - cx) / fx, sz * (height - 1 - cy) / fy, sz);
            glVertex3f(sz * (width - 1 - cx) / fx, sz * (height - 1 - cy) / fy, sz);
            glVertex3f(sz * (0 - cx) / fx, sz * (height - 1 - cy) / fy, sz);
            glVertex3f(sz * (0 - cx) / fx, sz * (height - 1 - cy) / fy, sz);
            glVertex3f(sz * (0 - cx) / fx, sz * (0 - cy) / fy, sz);
            glVertex3f(sz * (0 - cx) / fx, sz * (0 - cy) / fy, sz);
            glVertex3f(sz * (width - 1 - cx) / fx, sz * (0 - cy) / fy, sz);
            glEnd();
            glPopMatrix();
        }

        // points
        glPointSize(2);
        glBegin(GL_POINTS);
        for (size_t i = 0; i < points.size(); i++) {
            glColor3f(0.0, points[i][2]/4, 1.0-points[i][2]/4);
            glVertex3d(points[i][0], points[i][1], points[i][2]);
        }
        glEnd();

        pangolin::FinishFrame();
        usleep(5000);   // sleep 5 ms
    }
}

最后

以上就是稳重羽毛为你收集整理的SLAM——入门到放弃：g2o定义边初步认识g2o的边定义g2o的边向图中添加边实践.的全部内容，希望文章能够帮你解决SLAM——入门到放弃：g2o定义边初步认识g2o的边定义g2o的边向图中添加边实践.所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。