深度学习——L1及L2范数

在深度学习中，监督类学习问题其实就是在规则化参数同时最小化误差。最小化误差目的是让模型拟合训练数据，而规则化参数的目的是防止模型过分拟合训练数据。

参数太多，会导致模型复杂度上升，容易过拟合，也就是训练误差小，测试误差大。因此，我们需要保证模型足够简单，并在此基础上训练误差小，这样训练得到的参数才能保证测试误差也小，而模型简单就是通过规则函数来实现的。
 

L1范数和L2范数的差别

一个是绝对值最小，一个是平方最小：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。

L1范数

L1范数是指向量中各个元素绝对值之和，也有个美称叫“稀疏规则算子”。简而言之，即使参数值接近于零。在原始的代价函数后面加上一个L1正则化项，即所有权重w的绝对值的和，乘以λ/n。如下：

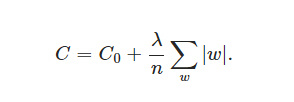
同样计算导数得：

 上式中sgn(w)表示w的符号。那么权重w的更新规则为：​

 比原始的更新规则多出了η * λ * sgn(w)/n这一项。当w为正时，更新后的w变小。当w为负时，更新后的w变大——因此它的效果就是让w往0靠，使网络中的权重尽可能为0，也就相当于减小了网络复杂度，防止过拟合。

另外，上面没有提到一个问题，当w为0时怎么办？当w等于0时，|W|是不可导的，所以我们只能按照原始的未经正则化的方法去更新w，这就相当于去掉η*λ*sgn(w)/n这一项，所以我们可以规定sgn(0)=0，这样就把w=0的情况也统一进来了。（在编程的时候，令sgn(0)=0,sgn(w>0)=1,sgn(w<0)=-1）

L2正则化

对于L2正则化：C=C0+λ2n∑iω2iC=C0+λ2n∑iωi2，相比于未加正则化之前,权重的偏导多了一项λnωλnω，偏置的偏导没变化，那么在梯度下降时ωω的更新变为：

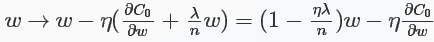
可以看出ωω的系数使得权重下降加速，因此L2正则也称weight decay(caffe中损失层的weight_decay参数与此有关)。对于随机梯度下降(对一个mini-batch中的所有x的偏导求平均)：

对于L1正则化：C=C0+λn∑i|ωi|C=C0+λn∑i|ωi|，梯度下降的更新为：

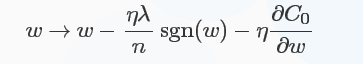
符号函数在ωω大于0时为1，小于0时为-1，在ω=0ω=0时|ω||ω|没有导数，因此可令sgn(0)=0，在0处不使用L1正则化。
L1相比于L2，有所不同：

• L1减少的是一个常量，L2减少的是权重的固定比例
• 孰快孰慢取决于权重本身的大小，权重刚大时可能L2快，较小时L1快
• L1使权重稀疏，L2使权重平滑，一句话总结就是：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0

实践中L2正则化通常优于L1正则化。

最后

以上就是美好蛋挞为你收集整理的深度学习——L1及L2范数的全部内容，希望文章能够帮你解决深度学习——L1及L2范数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。