♥注:未经博主同意,不得转载。
多项式的表示与求和是线性表应用的典型案列。
在数学上,一元多项式P(x)的表示为:
P(x)=a0+a1x+a2x2+…+anxn
其中,n为大于或等于0的整数,表示x的幂:ao,a1,…an为系数,an≠0,a0,a1,…,an-1可以为0,也可以不为0。
一元多项式的表示
为了表示一元多项式,可以将其所有项的系数用一个线性表来表示:(a0,a1,…,an)。这个线性表可以使用顺序存储结构或链式存储结构来存储,从而进行多项式的有关运算。若采用顺序存储结构,可使用一个一维数组存储这个线性表,即多项式的系数,而相应的幂则使用数组下标来表示。
一元多项式的顺序存储结构如下:
1 typedef int DataType; 2 const int MaxPolySize=100; 3 4 class Polyn 5 { 6 private: 7 DateType data[MaxPolySize]; 8 int size; //元素的个数 9 10 public: 11 Polyn(){size = 0;} //构造一个空多项式 12 ~Polyn(); 13 14 void Clear(){size=0;} //清空 15 Polyn sum(Polyn a); //多项式相加 16 Polyn sub(Polyn a); //多项式相减 17 };
但多项式的顺序存储有一个缺点:当存储形如P(x)=1+10x99的多项式时,由于a1到a98均为0,所以用来存储一元多项式的一维数组中的绝大部分单元存储的值都是0,导致存储效率低下,造成存储空间的浪费。因此,一般采用链式存储结构来描述一元多项式。
一元多项式的链式存储必须显式地表达系数值和幂值,这是由于链式存储打破了顺序存储中原有的幂与数组下标间的一一对应关系,一元多项式的项的结点结构表示如图所示。
一元多项式的链式存储结构表示如下:
1 2 struct term 3 { 4 double coef; //系数 5 int expn; //指数 6 }; 7 struct PNode 8 { 9 term data; 10 PNode *next; 11 }; 12 class Ployn 13 { 14 PNode *phead; 15 public: 16 Polyn() 17 { //构造函数 18 phead =new PNoed; 19 if(phead= =NULL) 20 exit(0); 21 phead->next=NULL; 22 } 23 ~Polyn(); //析构函数 24 25 void PolynAdd(Ployn Pa,Ployn Pb); //两个多项式相加 26 void Print(); //打印多项式 27 void Create(); //建立多项式 28 }; 29
一元多项式的求和
本节以多项式的加法为例,讲述一元多项式操作的实现。假设有一元n次多项式Pn(x)和一元m次多项式Qm(x),它们的系数可分别用线性表P=(p0,p1,…,pn)和Q=(q0,q1,…,qm)来表示。不失一般性,设m<n,则两个多项式相加的结果Rn(x)=Pn(x)+Qm(x)可以表示为线性表R=(p0+q0,p1+q1,p2+q2,…,pm+qm,pm+1,…,pn)。由于做加法的一元多项式的项的幂值可能变化很大,如1+2x500+4x5000,因此,我们采用链式存储结构来存储一元多项式。
根据给出的一元多项式的链式存储结构定义,给出一元多项式的加法的算法如下:
1 void Polyn::PolynAdd(Polyn Pa,Polyn Pb) 2 { 3 PNode *t1,*t2,*t3; 4 t1=Pa.phead->next; //t1指向Pa 5 t2=Pb.phead->next; //t2指向Pb 6 t3=phead; 7 8 while(t1&&t2) 9 { 10 if(t1->data.expn<t2->data.expn) //t1所指数据小于t2所指数据 11 { 12 t3->next=new PNode; 13 t3=t3->next; 14 t3->data=t1->data; 15 t1=t1->next; 16 }//t1插入到t3中 17 else if(t1->data.expn>t2->data.expn) 18 { t3->next=new PNode; 19 t3=t3->next; 20 t3->data=t2->data; 21 t2=t2->next; 22 }//将t2插入到t3中 23 else 24 { 25 double a=t1->data.coef+t2->data.coef; //指数相等 26 if(a) 27 { 28 t3->next=new PNode; 29 t3=t3->next; 30 t3->data.coef=a; 31 t3->data.expn=t1->data.expn; 32 } 33 t1=t1->next;//t1往后移 34 t2=t2->next;//t2往后移 35 } 36 } 37 38 while(t1!=NULL)//将t1剩余结点复制到t3中 39 { 40 t3->next=new PNode; 41 t3=t3->next; 42 t3->data=t1->data; 43 t1=t1->next; 44 } 45 while(t2!=NULL)//将t2剩余结点复制到t3中 46 { 47 t3->next=new PNode; 48 t3=t3->next; 49 t3->data=t2->data; 50 t2=t2->next; 51 } 52 t3->next=NULL; 53 } 54 55 //建立多项式 56 void Polyn::Create() 57 { 58 PNode *p,*q; 59 int n; 60 q=phead; 61 cout<<"请输入多项式的项数:"<<endl; 62 cin>>n; 63 if(n>0) 64 { 65 cout<<"请输入多项式各项的系数和指数:"<<endl; 66 for(int i = 0;i < n; ++i) 67 { 68 p=new PNode; 69 cin>>p->data.coef>>p->data.expn; 70 p->next=NULL; 71 q->next=p; 72 q=p; 73 } 74 } 75 } 76 77 //输出多项式 78 void Polyn::Print() 79 { PNode *p; 80 p=phead->next; 81 cout<<endl; 82 while(p) 83 { 84 cout<<p->data.coef<<" "<<p->data.expn<<endl; 85 p=p->next; 86 } 87 cout<<endl; 88 } 89 //析构函数:释放链表 90 Polyn::~Polyn() 91 { //析构函数 92 PNode *p,*q; 93 p=phead->next; //p指向第一个数据结点 94 while(p) 95 { 96 q=p; 97 p=p->next; //p指向下一个数据结点 98 delete q; //释放q所指的数据结点 99 } 100 phead->next=NULL; //头结点也释放 101 }
测试函数则放在main函数里:
1 int main() 2 { 3 Polyn Pa,Pb,Pc; //定义三个多项式 4 Pa.Create(); //建立多项式Pa 5 Pb.Create(); //建立多项式Pb 6 Pc.PolynAdd(Pa,Pb); //Pa与Pb相加得到Pc 7 cout<<endl<<"多项式相加得"; 8 Pc.Print(); //打印Pc 9 10 return 0; 11 }
测试情况如下: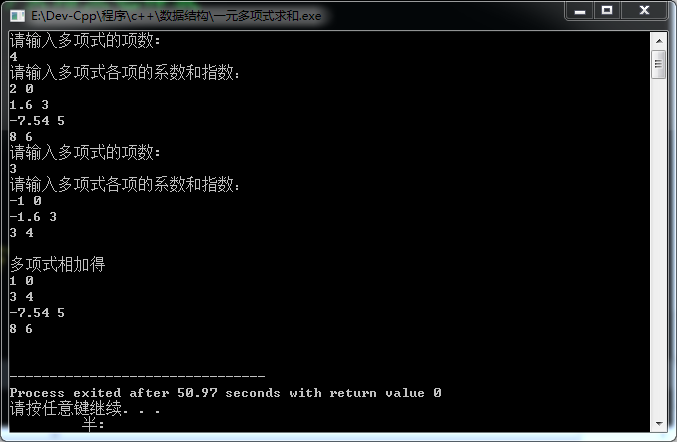
转载于:https://www.cnblogs.com/tenjl-exv/p/7479380.html
最后
以上就是暴躁滑板最近收集整理的关于线性表——一元多项式的求和的全部内容,更多相关线性表——一元多项式内容请搜索靠谱客的其他文章。








发表评论 取消回复