例题:买米换成买水果,袋子变成10斤,水果为苹果,香蕉,菠萝,三种水果每种只有1个,重量分别为
4,5,7 ,价值分别为 4,5,8;水果不可切开,请问如果装水果才能价值最大化。
解析:很明显这时候用我们的贪心思路已经不行了。我们按平均价值来说肯定是菠萝大,先选菠萝,装不下其他,这样装的水果价值只有8,而我们选择装两个小的,价值却可以达到9。那对于这种不可分割的单个物品来说,我们该如何去抉择呢。
方法1:穷举法。首先我们想到的肯定是穷举法,把所有装的情况列出来看看那一种方法价值最大,那就是我们要的结果。这样当然可以,但是当水果种类非常多的时候,情况数量会非常多,那我们要想更好一点的办法来应对数据很多的情况。
方法2:动态规划-递归。
我们知道穷举法的情况有2*2*2=8种,如果我们能把乘变成加,2+2+2=6,或者部分变成加法,那情况就会减少。
value[n],weight[n],sum,n,cap//value表示水果的价值,weight表示水果的重量,sum表示袋子装的水果的总价值,n表示水果种数,cap表示袋子容量。
zg那我们要开始设计我们的递归函数,假设函数名叫bag(),因为我们需要对所有水果进行判断是否拿,并且需要知道我们正在判断第几种水果,那么参数就需要水果种数n,bag(int n)。水果的重量和价值肯定要用到,但是这个我们可以放在全局变量,省的在函数中重复写。袋子里水果的总价值sum这是我们需要得到的结果,那就是返回值。袋子的容量我们肯定也是需要的。那函数雏形就出来了, int bag(int n,int cap)。这个函数的作用是求出有n种水果的时候,袋子容量为cap,装的水果价值最大是多少
int bag(int n,int cap)
{//假设现在n是3,cap是10,我们要怎么求bag(3,10)呢?怎么得到bag(3,10)呢,我们可以想到如果第三种水果我们没有选中,那么bag(3,10)是不是和bag(2,10)是一样的,都是在前两种水果里挑选也就是bag(3,10)=bag(2,10)。如果第三种水果选中了,那么这个袋子容量10,是不是有一部分被第三种水果占了,剩下的容量就是10-weight[2],那么我们是不是要用剩下的容量在前两种水果里挑选,那么这时候,bag(3,10)=bag(2,10-weight[2])+value[2],那我们的递推公式出来了。
#define max(x,y) x>y?x:y
int bag(int n,int cap)
{
return max(bag(n-1,cap),(bag(n-1,cap-w[n-1])+v[n-1]));
}
//当然递归要有边界,于是我们给他加上边界,参数有两个,所以边界也有两个,也就是n为1的时候和袋子容量不够的时候。
n为1时:
if(n==1)
if(cap>=w[0])
return v[0];
else return 0;
袋子容量不够的时候:
if(cap<w[n-1])
return bag(n-1,cap);
综合起来,我们的函数就写好了。
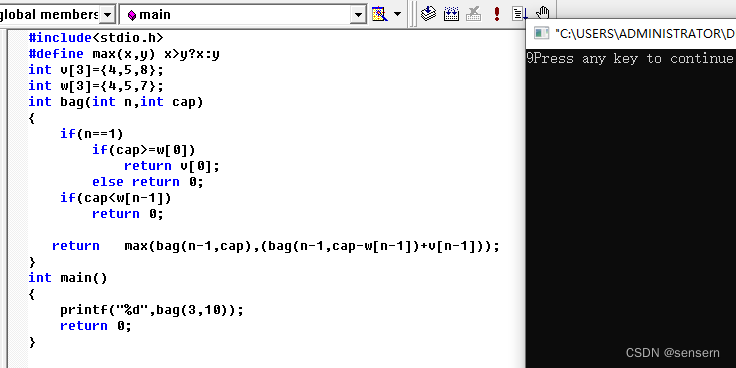
未完待续。
已修改部分错误,袋子容量不够时 return 0换成 return bag(n-1,cap)。
最后
以上就是整齐猎豹最近收集整理的关于贪心算法续(01背包)的全部内容,更多相关贪心算法续(01背包)内容请搜索靠谱客的其他文章。








发表评论 取消回复