概述
一、Jensen不等式
若f为区间I上的凹函数，则Jensen不等式成立：
这里若函数f为凹函数，则有：
凹函数（上凸）如下图所示：
归纳证明：
二、信息论
1.熵（信息不确定性度量）
2.联合熵
3.条件熵
条件熵的另一种表达方式
4.互信息（信息增益）
两个随机变量X， Y的互信息，定义为X，Y的联合分布和独立分布乘积的相对熵。
5.相对熵
设p(x)、 q(x)是X中取值的两个概率分布， 则p对q的相对熵是
说明：
相对熵可以度量两个随机变量的“距离” 。一般的， D(p||q) ≠D(q||p)、D(p||q)≥0、 D(q||p) ≥0
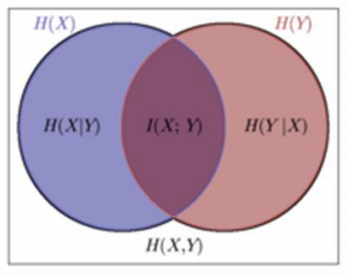
三、总结
H(X|Y) = H(X,Y) - H(Y)
H(X|Y) = H(X) - I(X,Y)
H(Y|X)= H(X,Y) - H(X)
H(Y|X)= H(Y) - I(X,Y)
I(X,Y)= H(X) + H(Y) - H(X,Y)
H(X|Y) ≤H(X) ， H(Y|X) ≤H(Y)
最后
以上就是现实灰狼为你收集整理的各种信息熵(Information entropy)的计算方法的全部内容，希望文章能够帮你解决各种信息熵(Information entropy)的计算方法所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
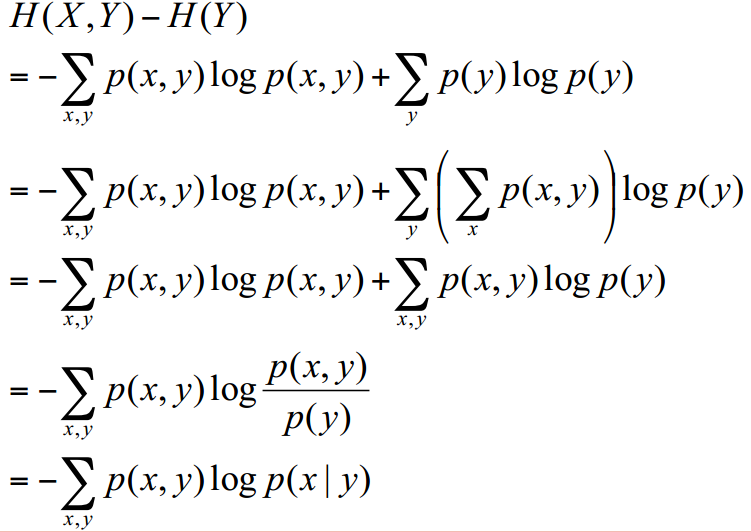
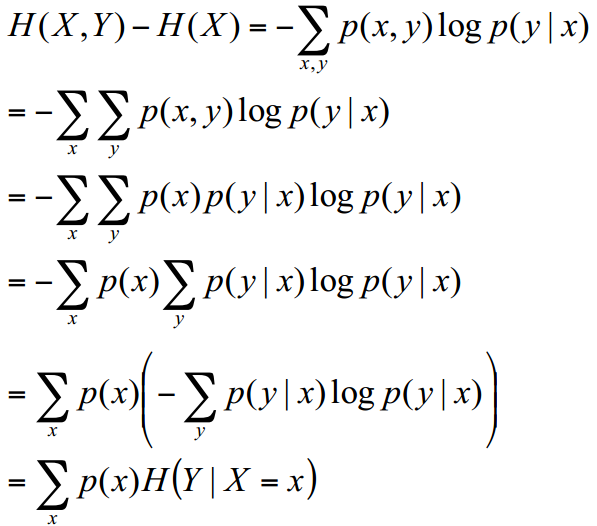
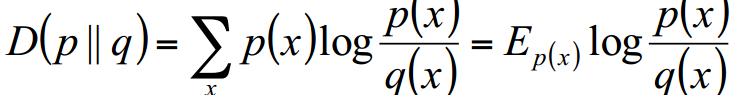
发表评论 取消回复