POJ - Picture(线段树&扫描线)

51 阅读 0 评论 34 点赞

我是靠谱客的博主温婉百合，最近开发中收集的这篇文章主要介绍POJ - Picture(线段树&扫描线)，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目链接http://poj.org/problem?id=1177
Time Limit: 2000MS Memory Limit: 10000K

Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.

Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1

The corresponding boundary is the whole set of line segments drawn in Figure 2.

The vertices of all rectangles have integer coordinates.

Input

Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.

0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.

Output

Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.

Sample Input

7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16

Sample Output

228

Problem solving report:

Description: 有多个矩形，矩形的两边平行于坐标轴，这些矩形之间可能存在相互覆盖，求周长。
Problem solving: 记录每个矩形的两条竖边（x1，y1，y2）和（x2，y1，y2），将所有的竖边按照x从小到大排序，然后一条一条竖边开始计算周长，那么以竖边所在的垂直于x轴的直线即是扫描线。每次移动到一条新的竖边的时候，我们需要计算所在竖边扫描线上有用边长（即当前竖边的有用部分，可能当前的竖边被覆盖部分），以及加上当前扫描线与上一条扫描线之前的横边长 * 横边条数，一直计算到最后一条竖边，即是完整周长了。
用线段树做，线段树存储的是y轴的覆盖情况，每个节点存储4个信息:

当前节点被覆盖的长度;
当前节点至少被完全覆盖多少次(这个没必要下放);
当前节点的最左端和最右端分别是否被覆盖;
当前节点有多少个不连续的覆盖区域。

初始化所有节点所有变量为0，然后从下到上遍历每个扫描线，依次更新并求出相邻两条扫描线之间的周长，周长包括竖边和横边，其中横边长为｜更新后线段树总覆盖区域－更新前线段树总覆盖区域｜，竖边总长为更新前不连续覆盖区域个数×(相邻扫描线的y坐标差)×2.
见下图：
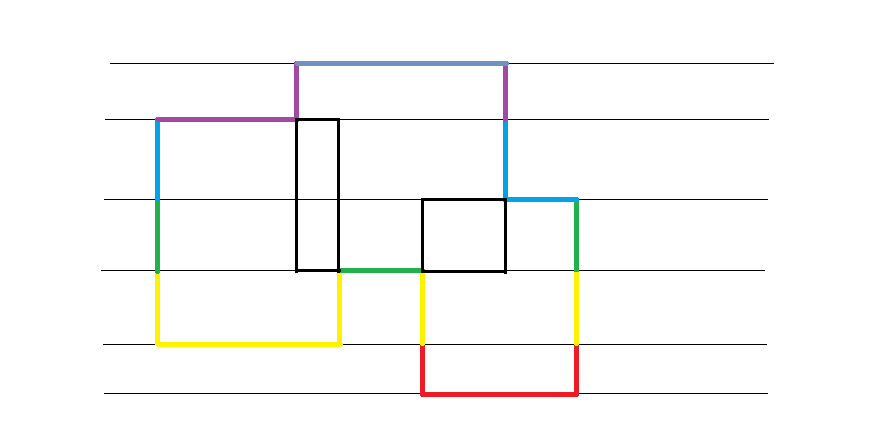
在这里插入图片描述

如上图是由三个矩阵组成的，每扫描一次就可计算出同种颜色的长度，其中黑线是不用计算的。

Accepted Code:

/* 
 * @Author: lzyws739307453 
 * @Language: C++ 
 */
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define lson rt << 1
#define rson rt << 1 | 1
using namespace std;
const int MAXN = 5e3 + 5;
const int MAXM = 2e4 + 5;
const int inf = 0x3f3f3f3f;
struct edge {
    int l, r, h, v;
    edge() {}
    edge(int l, int r, int h, int v) : l(l), r(r), h(h), v(v) {}
    bool operator < (const edge &s) const {
        return s.h > h;
    }
}p[MAXN << 1];
struct Tree {
    bool ls, rs;
    int len, num, v;
}seg[MAXM << 2];
void pushup(int l, int r, int rt) {
    if (seg[rt].v) {
        seg[rt].ls = seg[rt].rs = 1;
        seg[rt].len = r - l + 1;
        seg[rt].num = 1;
    }
    else {
        if (!(r - l)) {
            seg[rt].ls = seg[rt].rs = 0;
            seg[rt].len = seg[rt].num = 0;
        }
        else {
            seg[rt].ls = seg[lson].ls;
            seg[rt].rs = seg[rson].rs;
            seg[rt].len = seg[lson].len + seg[rson].len;
            seg[rt].num = seg[lson].num + seg[rson].num - (seg[lson].rs & seg[rson].ls);
        }
    }
}
void Update(int Ql, int Qr, int v, int l, int r, int rt) {
    if (Ql <= l && Qr >= r) {
        seg[rt].v += v;
        pushup(l, r, rt);
        return ;
    }
    int mid = l + (r - l >> 1);
    if (Ql <= mid)
        Update(Ql, Qr, v, l, mid, lson);
    if (Qr > mid)
        Update(Ql, Qr, v, mid + 1, r, rson);
    pushup(l, r, rt);
}
int main() {
    int n;
    int x1, y1, x2, y2;
    scanf("%d", &n);
    int l = inf, r = -inf;
    for (int i = 0; i < n; i++) {
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        l = min(l, x1), r = max(r, x2);
        p[i << 1] = edge(x1, x2, y1, 1);
        p[i << 1 | 1] = edge(x1, x2, y2, -1);
    }
    int size = n << 1;
    sort(p, p + size);
    int ans = 0, last = 0;    
    memset(seg, 0, sizeof(seg));
    for (int i = 0; i < size; i++) {
        Update(p[i].l, p[i].r - 1, p[i].v, l, r, 1);
        ans += abs(seg[1].len - last) + (p[i + 1].h - p[i].h) * seg[1].num * 2;
        last = seg[1].len;
    }
    printf("%dn", ans);
    return 0;
}