浅谈神经网络语言模型(NNLM)的理解

    最近一直在使用各种Embedding的方法，于是好奇的看到了NNLM，总结一下自己的理解。

Forward

  首先，我们假设一句话由$w=(w_1,w_2,...,w_t)$组成（$w_i$为单词），在语言模型中计算一句话的概率，我们用$w_1,w_2,...,w_t$的联合概率来表示一句话的概率。如下：

$$\mathbf{p}(\mathbf{w})=\mathbf{p}=({\mathbf{w}}_1,{\mathbf{w}}_2,...,{\mathbf{w}}_{\mathbf{t}})\text{\hspace{1em}(1)}$$

也可以来判断一句话是否通顺，都是一个意思，通过条件概率得到如下变形：
$$\begin{array}{ll}P(w_1,w_2,\dots ,w_t)& =P(w_t|w_{t-1},\dots ,w_2,w_1)\ast P(w_{t-1},\dots ,w_2,w_1)\\ & \\ & =p(w_1)\ast p(w_2|w_1)\ast p(w_3|w_1,w_2)\ast ......\ast p(w_n|w_1,......,w_{n-1})\end{array}\text{\hspace{1em}(2)}$$

根据马尔可夫假设,我们可以类似的认为离t最近n-1个词和它相关，从而可以得到：

$$\mathbf{P}({\mathbf{w}}_{\mathbf{t}}|{\mathbf{w}}_{\mathbf{t}-1},\dots ,{\mathbf{w}}_2,{\mathbf{w}}_1)=\mathbf{P}({\mathbf{w}}_{\mathbf{t}}|{\mathbf{w}}_{\mathbf{t}-1},{\mathbf{w}}_{\mathbf{t}-2},\dots ,{\mathbf{w}}_{\mathbf{t}-\mathbf{n}+1})\text{\hspace{1em}(3)}$$
另外，插一点题外话，若我们这里认为只和最近的1个词相关，便成了2-gram，同时我们可以把公式（2）变形如下：
$$\begin{array}{ll}P(w_1,w_2,\dots ,w_t)& =P(w_t|w_{t-1},\dots ,w_2,w_1)\ast P(w_{t-1},\dots ,w_2,w_1)\\ & \\ & =p(w_1)\ast p(w_2|w_1)\ast p(w_3|w_1,w_2)\ast ......\ast p(w_n|w_1,......,w_{n-1})\\ & \\ & =p(w_1)\ast p(w_2|w_1)\ast p(w_3|w_2)\ast ......\ast p(w_n|w_{n-1})\end{array}\text{\hspace{1em}(2*)}$$

  回归正题，我们这里假设词典为10000个词。分别对语料中的词进行one-hot编码（词典为语料中不重复的单词）。
  一般来说，这个n是一个比较小的值。我们这里假设n=6，那么n-1=5.那么，我们可以认为输入是5个one-hot向量，我们把这个向量拼成一个[5 * 10000]的矩阵，由于向量的维度通常比较高，我们进行降维处理：右乘一个[10000 *100]的权重矩阵得到一个[5 * 100]的矩阵（这里不一定是100，只是举个例子）。

  上面的这一段在原文里面其实是没有的，这样讲解是为了更好的理解，论文里面是通过index在C中进行一个查表操作。其实道理是一样的。

  这个过程我们也可以理解为从one-hot到distributed representation的转化过程。这样就得到了特征向量。根据论文 Nerual Network Language Model写道：

a function g maps an input sequence of feature vectors for words in context,$(C(w_{t-n+1}),\cdot \cdot \cdot ,C(w_{t-1}))$, to a conditional probability distribution over words in V for the next word $w_t$

上面的$(C(w_{t-n+1}),\cdot \cdot \cdot ,C(w_{t-1}))$就是我们得到的特征向量，作者通过一个映射g来得到对$w_t$.的预测，

这个映射的设计结构如下图：

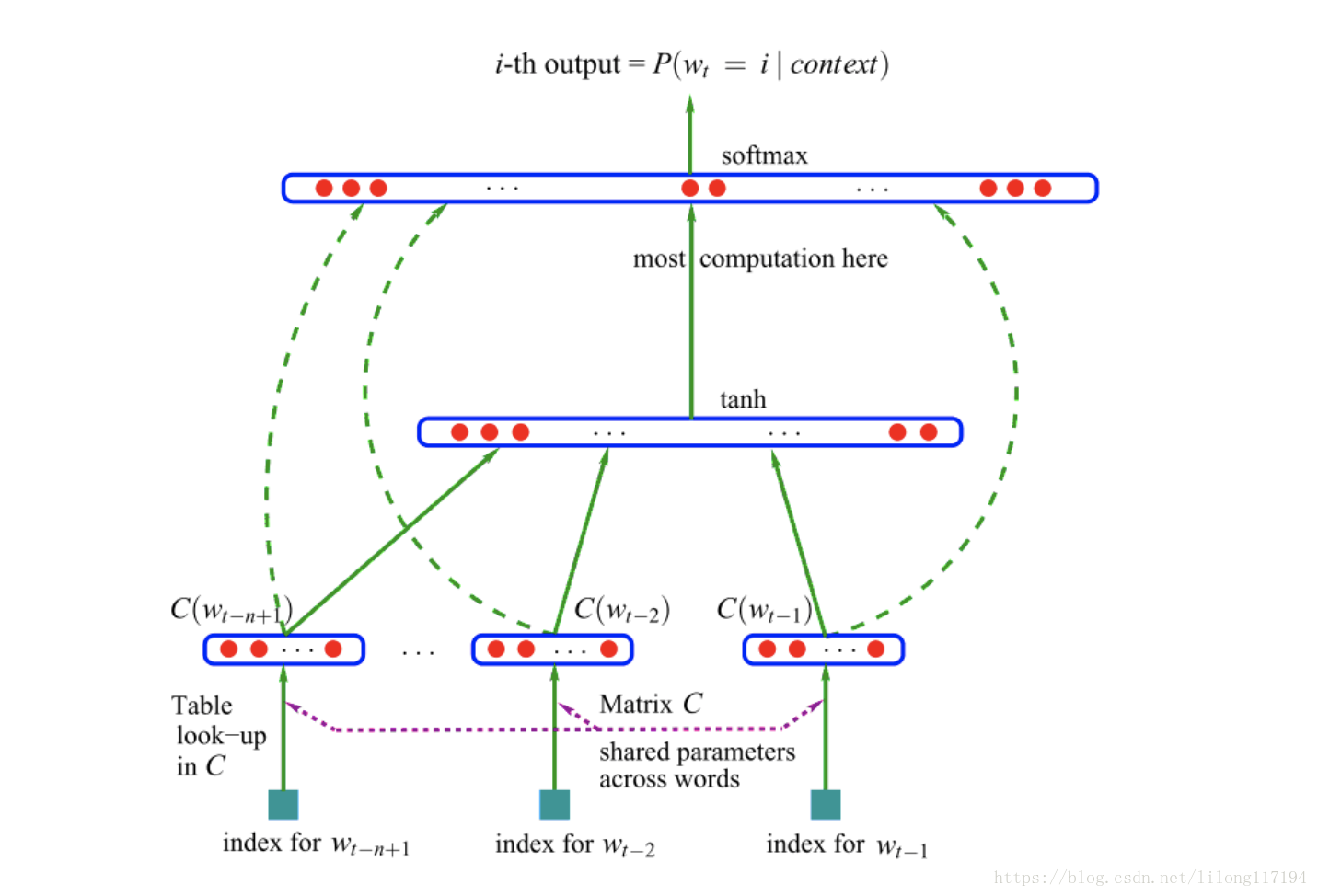
  先是将特征向量进行拼接，也就是5*100的矩阵，拼接成一个500维的向量($x$)，然后将这个向量($x$)

经过 (4) 线性变换之后，再经过tanh处理得到一个100维的向量,如（5）：

$${\mathbf{y}}_1=\mathbf{U}\mathbf{t}\mathbf{a}\mathbf{n}\mathbf{h}(\mathbf{d}+\mathbf{H}\mathbf{x})\text{\hspace{1em}(4)}$$

$$[100\ast 500]\ast [500\ast 1]=[100\ast 1]\text{\hspace{1em}(5)}$$

  然后左乘U得到 一个10000维的向量 $y_1$,如（6）：
$$[10000\ast 100]\ast [100\ast 1]=[10000\ast 1]\text{\hspace{1em}(6)}$$
  接下来是对输入特征向量($x$)的处理 ,($x$)左乘一个[10000 * 500]的矩阵得到一个[10000 * 1]的向量：
$${\mathbf{y}}_2=\mathbf{b}+\mathbf{W}\mathbf{x}\text{\hspace{1em}(7)}$$

$$[10000\ast 500]\ast [500\ast 1]=[10000\ast 1]\text{\hspace{1em}(8)}$$

  将上面$y_1和y_2$相加就得到了最终的向量
$$\mathbf{y}={\mathbf{y}}_1+{\mathbf{y}}_2\text{\hspace{1em}(9)}$$

$$\mathbf{y}=\mathbf{b}+\mathbf{W}\mathbf{x}+\mathbf{U}\mathbf{t}\mathbf{a}\mathbf{n}\mathbf{h}(\mathbf{d}+\mathbf{H}\mathbf{x})\text{\hspace{1em}(10)}$$
  $y$是一个10000的向量,这里的x为特征向量，$W，U,H都为权重，b,d为bias$。然后通过softmax得到对$w_t$的预测：

$$\mathbf{P}({\mathbf{w}}_{\mathbf{t}}|{\mathbf{w}}_{\mathbf{t}-1},\cdot \cdot \cdot {\mathbf{w}}_{\mathbf{t}-\mathbf{n}+1})=\frac{{\mathbf{e}}^{\mathbf{y}{}_{\mathbf{w}}{}_{,}{}_{\mathbf{i}}}}{{\sum }_{\mathbf{i}}^{\mathbf{N}}{\mathbf{e}}^{{\mathbf{y}}_{\mathbf{w}}{{}_{,}}_{\mathbf{i}}}}\text{\hspace{1em}(11)}$$
也就是当上下文为content($w$)时，$w_t$为字典中第i个词的概率。

Back propagation

损失函数： $$\mathbf{L}=\sum _{\mathbf{w}\in \mathbf{c}}\mathbf{l}\mathbf{o}\mathbf{g}\mathbf{p}(\mathbf{w}|\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{t}\mathbf{e}\mathbf{x}\mathbf{t}(\mathbf{w}))\text{\hspace{1em}(12)}$$

接下来对目标函数进行梯度上升求解即可。

最后

以上就是悲凉康乃馨为你收集整理的浅谈神经网络语言模型(NNLM)的理解的全部内容，希望文章能够帮你解决浅谈神经网络语言模型(NNLM)的理解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。