最近在看recast&detour源码的时候有遇到许多数学上的算法问题,特此记录,以便以后查看。
方法
思路:
过这一点向右做一条水平射线,看这射线和多边形的几条边有交点。如果边的条数为奇数则说明点在多边形内。
(也可过这点向左,向上,向下做一条射线)
具体:
对每一条边和点进行如下判断,看是否满足下面两个条件,若均满足,则定义此边和射线有交点。设边为vj->vi,点为 pt :
1)点pt 的纵坐标是否满足式子: (vi[1] > pt[1]) != (vj[1] > pt[1])
即 pt 纵坐标是否满足[vj[1], vi[1]),如果 vj[1] > vi[1],那么[vi[1], vj[1]) ,即是否满足低闭高开。
2)再判断点pt 是否在 边所在的直线的 左边。
列出边的标准方程 x = ky + b ,把 pt的纵坐标带入,得到x的值, 如果是大于 pt 的横坐标,那么说明 点pt 在边所在的直线的 左边。【不需要考虑 y = b 的水平线的方程,因为如果边是水平线 和 点 在同一条直线上,上面的第一个条件就不满足】
图示:
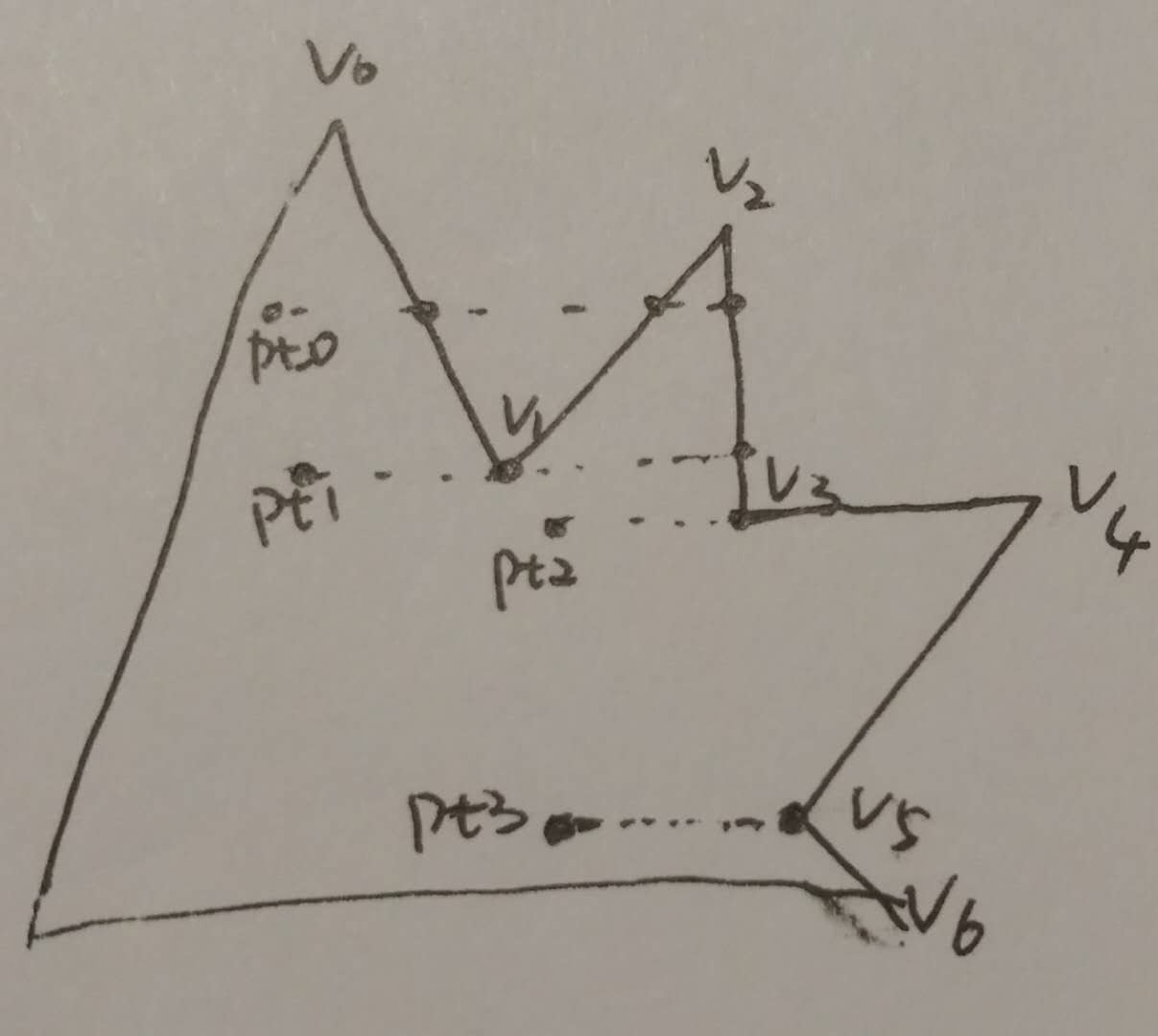
如下图 有三个特殊点pt1 pt2 pt3,根据上面判断方法,均能正确得到在多边形内的结论,即满足条件的边为奇数个。
pt0是一个正常点, 满足条件的边为v0v1 v1v2 v2v3,3条。
pt1是一个特殊点,满足条件的边为v0v1 v1v2 v2v3,3条。pt1与v1点在同一条水平线上,v0v1 和 v1v2 均满足第一个条件(一个等于,一个大于,低闭高开),v2v3正常满足。
pt2是一个特殊点,满足条件的边为v2v3,1条。pt2与v3点 v4点在同一条水平线上,v3v4不满足第一个条件(均等于),v4v5不满足第一个条件(一个等于,一个小于)。
pt3是一个特殊点,满足条件的边为v4v5,1条。pt3与v5点在同一条水平线上,v5v6不满足第一个条件(一个等于,一个小于)。
源码
/// All points are projected onto the xz-plane, so the y-values are ignored.
bool dtPointInPolygon(const float* pt, const float* verts, const int nverts)
{
// TODO: Replace pnpoly with triArea2D tests?
int i, j;
bool c = false;
for (i = 0, j = nverts-1; i < nverts; j = i++)
{
const float* vi = &verts[i*3];
const float* vj = &verts[j*3];
if (((vi[2] > pt[2]) != (vj[2] > pt[2])) &&
(pt[0] < (vj[0]-vi[0]) * (pt[2]-vi[2]) / (vj[2]-vi[2]) + vi[0]) )
c = !c;
}
return c;
}参考
https://www.codeproject.com/Tips/84226/Is-a-Point-inside-a-Polygon
最后
以上就是沉静河马最近收集整理的关于判断点是否在多边形内(任意多边形)方法源码参考的全部内容,更多相关判断点是否在多边形内(任意多边形)方法源码参考内容请搜索靠谱客的其他文章。








发表评论 取消回复