[CF739B] Alyona and a tree 详解

53 阅读 0 评论 35 点赞

我是靠谱客的博主大胆钢铁侠，最近开发中收集的这篇文章主要介绍[CF739B] Alyona and a tree 详解，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

B. Alyona and a tree
Alyona has a tree with n vertices. The root of the tree is the vertex 1. In each vertex Alyona wrote an positive integer, in the vertex i she wrote ai. Moreover, the girl wrote a positive integer to every edge of the tree (possibly, different integers on different edges).

Let's define dist(v, u) as the sum of the integers written on the edges of the simple path from v to u.

The vertex v controls the vertex u (v ≠ u) if and only if u is in the subtree of v and dist(v, u) ≤ au.

Alyona wants to settle in some vertex. In order to do this, she wants to know for each vertex v what is the number of vertices u such that v controls u.

Input
The first line contains single integer n (1 ≤ n ≤ 2·105).

The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — the integers written in the vertices.

The next (n - 1) lines contain two integers each. The i-th of these lines contains integers pi and wi (1 ≤ pi ≤ n, 1 ≤ wi ≤ 109) — the parent of the (i + 1)-th vertex in the tree and the number written on the edge between pi and (i + 1).

It is guaranteed that the given graph is a tree.

Output
Print n integers — the i-th of these numbers should be equal to the number of vertices that the i-th vertex controls.

Examples
inputCopy
5
2 5 1 4 6
1 7
1 1
3 5
3 6
outputCopy
1 0 1 0 0
inputCopy
5
9 7 8 6 5
1 1
2 1
3 1
4 1
outputCopy
4 3 2 1 0
Note
In the example test case the vertex 1 controls the vertex 3, the vertex 3 controls the vertex 5 (note that is doesn't mean the vertex 1 controls the vertex 5).

有道是

算法就是优化的暴力

那么我们先从暴力开始说起(真的是最裸的暴力qwq).

首先这是棵树,很显然采用链式前向星建边.然后我们观察题面
qwq
显然,我们需要知道dis[u][v]的值,那么,怎么求他们的路径呢?

学了图论的应该都知道Dijkstra的优秀,那我们就采用Dijkstra吧!

跑一遍最短路,由于Dijkstra求的是单源最短路,所以我们得到了从根节点1到每个子节点的距离.那么问题来了

tm我们要的是dis[u][v] 你tm求个dis[1][k]有个屁用啊?!
qwq

稍安勿躁,我们先看一棵简单的树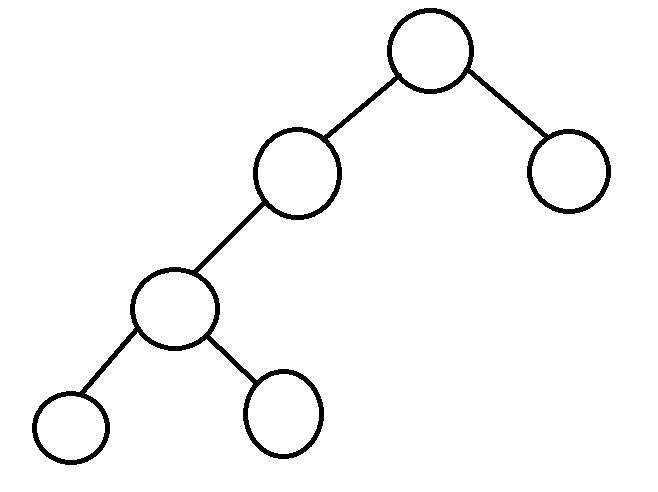
qwq
如果我们现在已知根节点到任意节点的单源最短路,想求任意子节点和父节点的距离怎么办?
就这么办!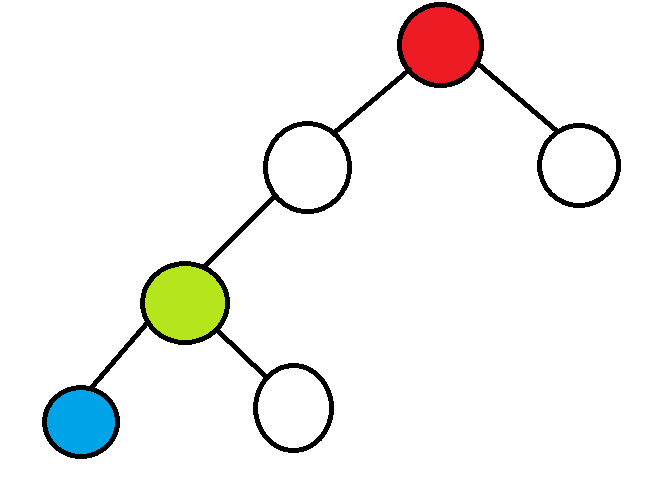
qwq

红色的是根节点,绿色是父节点,蓝色是子节点.
不难发现,dis[blue][green] = dis[red][blue] - dis[red][green]!
那么我们的单源最短路有用了!
---接下来呢?
当然是找每个点控制的点啦!
---怎么找呢?
开个father数组把每个点的直接父亲记录下来,链式遍历求每个点控制的个数啊!
就像这样

inline void isFa(int now,int son)
{
    rg int f = fa[now];
    if (!f) return;
    if (dis[son] - dis[f] <= pos[son])
    {
        ++ans[f];
        isFa(f,son);
    }
}

是不是很简略啊qwq
那么把上述部分拼凑一下,我们的代码就出炉啦

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
#define rg register
#define LL long long
const int maxn = 233333;
template <typename qwq> inline void read(qwq & x)
{
    x = 0;
    rg int f = 1;
    rg char c = getchar();
    while (c < '0' || c > '9')
    {
        if (c == '-') f = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9')
    {
        x = (x << 1) + (x << 3) + (c ^ 48);
        c = getchar();
    }
    x *= f;
}
template <typename qaq> inline void print(qaq x)
{
    if (x < 0)
    {
        putchar('-');
        x = -x;
    }
    if (x > 9) print(x / 10);
    putchar(x % 10 + '0');
}
struct edge
{
    int v,w,next;
}e[maxn];
int tot,head[maxn];
inline void add(int x,int y,int z)
{
    ++tot;
    e[tot].v = y;
    e[tot].w = z;
    e[tot].next = head[x];
    head[x] = tot;
}
int dis[maxn],ans[maxn],fa[maxn],pos[maxn];;
bool vis[maxn];
priority_queue <int,vector<int>,greater<int> > heap;
inline void dijkstra()
{
    memset(dis,0x3f,sizeof dis);
    dis[1] = 0;
//  vis[1] = 1;
    heap.push(1);
    while (!heap.empty())
    {
        rg int x = heap.top();
        heap.pop();
        if (vis[x]) continue;
        vis[x] = true;
        for (rg int i = head[x];i;i = e[i].next)
        {
            rg int v = e[i].v,w = e[i].w;
            if (dis[x] + e[i].w < dis[v])
            {
                dis[v] = dis[x] + e[i].w;
                heap.push(v);
            }
        }
    }
}
inline void isFa(int now,int son)
{
    rg int f = fa[now];
    if (!f) return;
    if (dis[son] - dis[f] <= pos[son])
    {
        ++ans[f];
        isFa(f,son);
    }
}
inline void dfs(int x,int fa)
{
    for (rg int i = head[x];i;i = e[i].next)
    {
        rg int v = e[i].v;
//      printf("Test x:%d,v:%d,fa:%dn",x,v,fa);
//      system("pause");
        if (v == fa) continue;
        dfs(v,x); 
        if (dis[v] - dis[x] <= pos[v])
        {
            ++ans[x];
            isFa(x,v);
        }
    }
}
int n,m,x,y,z;
int main()
{
//  freopen("tree.in","r",stdin);
//  freopen("tree.out","w",stdout);
    read(n);
    for (rg int i = 1;i <= n;++i) read(pos[i]);
    for (rg int i = 2;i <= n;++i)
    {
        read(x),read(y);
        add(x,i,y);
        fa[i] = x;
    }
    fa[1] = 0;
    dijkstra();
    dfs(1,0);
    for (rg int i = 1;i <= n;++i)
    {
        print(ans[i]),putchar(' ');
    }
}

然后开心的submit
qwq
qwq

怎么办一定是数据太强了

我们考虑优化一下吧...

首先!根本不用Dijkstra! 我们这是棵树,为什么不在dfs的时候把父亲节点的信息拿过来用呢?!

直接边跑dfs边求dis不就的了吗qwq

然后这个遍历求控制的节点数,万一我一棵树都能被根节点控制我岂不是要遍历1mol次这棵树?!

让我们思考一下,优化这种遍历次数一般用什么方法呢emm..

对了!二分和倍增嘛!

由于我们经常用二分,那么我们考虑一下二分算法.

首先从子节点出发,我们需要找到dis[1][son],然后除以二,这个点就是mid了,l是子节点,r是根节点(1).好的,到son的距离大约为dis[1][son] / 2的节点是...不慌我遍历一次不就知道了吗qwq.

等等,遍历.....

~~好的我们还是考虑倍增算法吧~~

倍增其实挺好实现,由于我们是始终只看当前点的father节点,所以找到最后肯定是根节点,那么这样遍历出来其实就是个长长的边而已(自己画图理解我懒得画了qwq)

从子节点出发,由p = 1(倍增倍数)开始倍增,找到一个点,若当前点可以实现,则更新当前节点并继续向上倍增,不行的话则缩小为p / 2,由更新后的节点继续倍增.时间复杂度类似于二分.

好了最后能优化的也就是一个一个加太慢了.那么有没有一款能实现区间修改的数据结构呢?

对,线段树!

我们考虑在原来的基础上套线段树并进行区间更新.

等等,我们这个树上的节点编号好像并不是连续的...

~~好的我们想一下其他办法吧~~

想想我们是不是学过差分数组了,对,我们就用树上差分实现吧!

本题所用的树上差分其实是简化版的,因为我们所有的节点都是在根节点(1)到son节点这条边上,不必再费心思求什么两点的LCA再进行差分.

举个栗子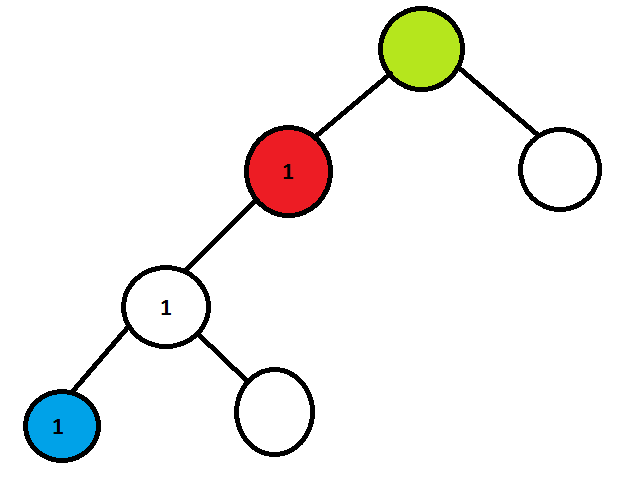
qwq

比如我们原来所有节点都代表0,我们想在从blue到red的地方+ 1.

那么我们只用在blue这个点上+ 1,在green这个点- 1,从blue到red求一次前缀和,用前缀和代表每个节点的信息即可.

拿出草稿算一下,是不是刚好+ 1呀qwq

那么这里也解决了.

好了,上最终代码!

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
#define rg register
#define LL long long
#define __space putchar(' ')
#define __endl putchar('n')
template <typename qwq> inline void read(qwq & x)
{
    x = 0;
    rg int f = 1;
    rg char c = getchar();
    while (c < '0' || c > '9')
    {
        if (c == '-') f = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9')
    {
        x = (x << 1) + (x << 3) + (c ^ 48);
        c = getchar();
    }
    x *= f;
}
template <typename qaq> inline void print(qaq x)
{
    if (x < 0)
    {
        putchar('-');
        x = -x;
    }
    if (x > 9) print(x / 10);
    putchar(x % 10 + '0');
}
struct edge
{
    int v,w,next;
}e[233333 << 1];
int tot,head[233333 << 1],ans[233333],a[233333],bz[233333][19];
//=================================================================
inline void add(int x,int y,int z)
{
    ++tot;
    e[tot].v = y;
    e[tot].w = z;
    e[tot].next = head[x];
    head[x] = tot;
}
LL dep[233333];
inline void dfs(int x,int fa,int w)
{
    bz[x][0] = fa;
    dep[x] = dep[fa] + w;
    for (rg int i = 1;i <= 18;++i)
    {
        bz[x][i] = bz[bz[x][i - 1]][i - 1];
    }
    for (rg int i = head[x];i;i = e[i].next)
    {
        rg int v = e[i].v,ww = e[i].w;
        if (v == fa) continue;
        dfs(v,x,ww);
        rg int pp = pos[v];
        if (ww > pp) continue;
        //=================================================================
        rg int p = 1;
        while(p && v)
        {
            if (dep[v] - dep[bz[v][p]] <= pp)
            {
                pp -= dep[v] - dep[bz[v][p]];
                v = bz[v][p];
                p <<= 1;
            }
            else p >>= 1;
        }
        if (dep[v] - dep[bz[v][0]] <= pp) v = bz[v][0];
        --ans[bz[v][0]],++ans[bz[e[i].v][0]];
        //=================================================================
    }
    ans[fa] += ans[x];
}
//=================================================================
int n,m,x,y,z;
int main()
{
    read(n);
    for (rg int i = 1;i <= n;++i)
    {
        read(a[i]);
    }
    for (rg int i = 2;i <= n;++i)
    {
        read(x),read(y);
        add(x,i,y);
        add(i,x,y);
    }
    dfs(1,0,0);
    for (rg int i = 1;i <= n;++i)
    {
        print(ans[i]),putchar(' ');
    }
}

Submit...

qwq