前言

这道题一开始思路错了,用了什么最小生成树搞了后数圈…..结果是状压DP…(没有观察啊！)

题目

传送门

给定一个简单图，输出其中的简单环的数目。简单环的含义是，不包含重复顶点、重复边的环。
输入
输入的第一行包含了两个整数 n 和 m (1 ≤ n ≤ 19, 0 ≤ m) – 分别表示图的顶点数目、边数目。以下 m 行的每行包含了两个整数 a 和 b, (1 ≤ a, b ≤ n, a ≠ b) 表示顶点 a 和 b 由一条无向边连接。任意一对顶点之间，不超过一条边相连。

输出
输出给定图中的简单环数目。

示例
输入
4 6
1 2
1 3
1 4
2 3
2 4
3 4
输出
7
备注
示例图是一个完全子图 (Clique, 又称为 团)，包含了长度为 3 的环 4 个，以及长度为 4 的环 3 个。
上面的图如下：

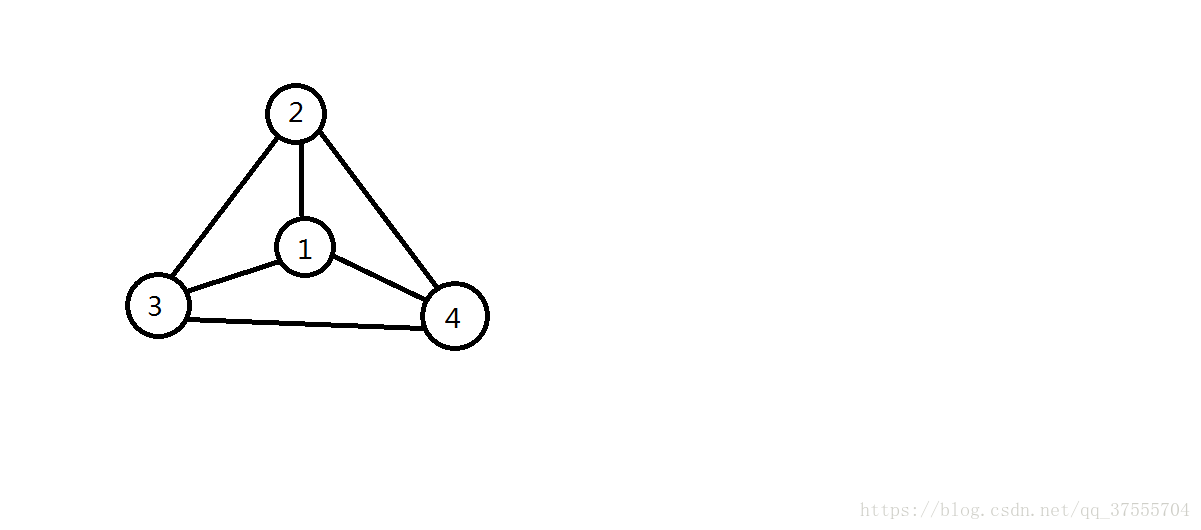
上面中{1-2-3},{1-3-4},{1-2-4},{1-3-4-2},{1-3-2-4},{1-2-4-3},{2-3-4}为7个圈

思路

既然已经说了是状压DP,我们来看看这样做的原因吧：
1.这里n最多只有19
2.很难用有关图论的知识解决
3.DFS、二进制枚举会超时,要优化
那我们让DP的一维来二进制枚举点,这应该比较容易想得到,然后或许会想到直接判断是否联通,但这是搜索枚举的方法
我们发现只用一维很难解决该问题,于是我们又多了一维：我们当前遍历到的点
那这样我们就可以不用DFS了
我们定义就是：
f[S][i]:点集S中当前遍历到i点的方案数 f [ S ] [ i ] : 点 集 S 中 当 前 遍 历 到 i 点 的 方 案 数 $f[S][i]:点集S中当前遍历到i点的方案数$
我们再枚举一$j$来表示下一个点(但这里刷表易懂),也就是枚举i所连的非该集合的点,要注意$j$不能在当前点集,那么状态转移方程式就可以出来了：
$f[S|(1<<j)][i]+=f[S][i]((1leq jleq n) and quad j∉S quad and quad i,j相连)$
当我们发现j为当前集合S回到起点时，就说明正好存在了环(之前肯定没有存在),就可以用ans答案了
但我们要注意初始化
显然我们知道的是当点集只有一个点时dp[S][i]为1,而其他情况就是0,也就是说我们只能从当前不为0的状态转移到其他状态.
But,
我们有一个很尴尬的问题,我们不知道起点的位置,而且答案算多了很多
假设我们就拿下面以图来试一下(S这里用二进制简写)：

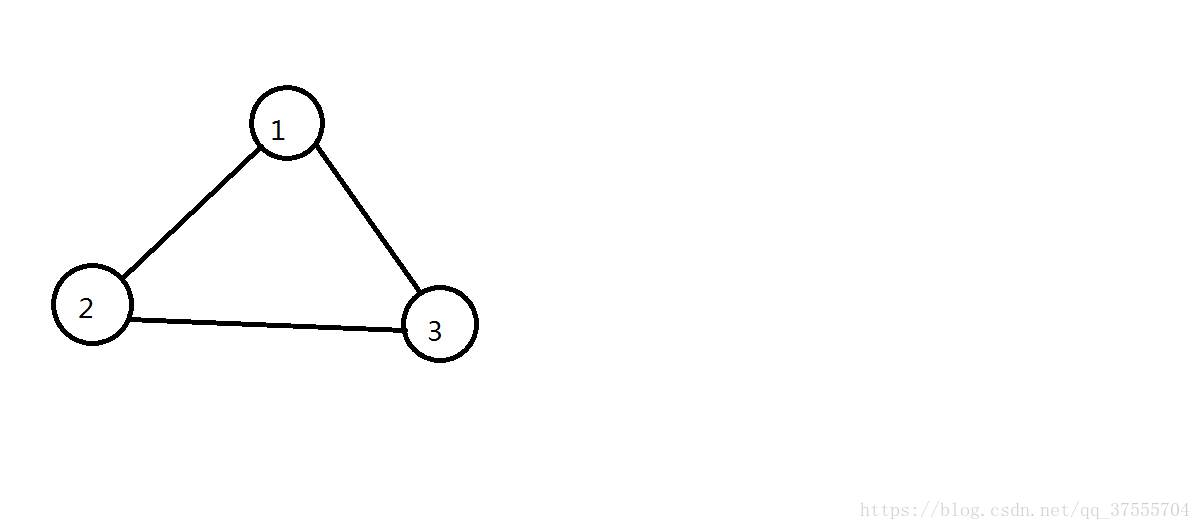
首先f[1][1]=f[10][1]=f[100][1]=1;
f[1][1]->(f[11][2]->f[111][3],f[101][3]->f[111][2])
f[10][2]->(f[11][1]->f[111][3],f[110][3]->f[111][1])
f[100][3]->(f[101][1]->f[111][2],f[110][2]->f[111][1])
所以算出来等于6…
我们可以发现,(控制变量法!!)当我们起点固定时,会跑出两个相同的圈,为什么会这样呢？？因为我们的DP会按顺时针找一遍圈,也会逆时针找一遍圈.所以,一个圈同一起点算重了两次,
而且我们又可以发现我们好像将圈上的每个点都当做了起点,那这就算重了很多次.
那我们可以令S中最靠右的点为起点,我在下面的代码中用lowbit获取了它的位置(用了树状数组中的名字,极为不专业…~)
有人可能会问,两个点会不会构成圈？我们来试一下：
就拿1,2来说:
f[1][1]=f[10][2]=1;(初始化)
f[1][1]->f[11][1];
因为这是二进制枚举,你的lowbit()函数找到一点后只会以这个点作为起点来找圈,也就是j只会不小于起点,如果j小于起点我们就会发现对于这个状态更新出的状态找lowbit()会变!，所以在上面f[10][2]->f[11][1]这种情况是不存在的！
所以两个点找圈只会算一次,而不会算两次！
那么最后答案就是:
（总答案-m条边）/2
好了,重要的说得差不多了,看一下代码吧,有注释的

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<set>
#include<map>
#include<ctime>
#include<queue>
#include<cmath>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long
using namespace std;
int read(){
    int f=1,x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}  
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    return x*f;
}
int n,m;
#define MAXN 19
#define INF 0x3f3f3f3f
int lowbit(int x){for(int i=0;i<n;i++)if(x&(1<<i))return i;}
bool Map[MAXN+5][MAXN+5];//lowbit(S):找S二进制中最低非零位的位置
LL f[(1<<MAXN)+5][MAXN+5];
int main(){//f[S][i]:点集S,此时访问到i点,起点为lowbit(S)
    LL ans=0;
    n=read(),m=read();
    for(int i=1;i<=m;++i){//这里以所有点以0开始会好弄一些
        int x=read()-1,y=read()-1;
        Map[x][y]=Map[y][x]=1;
    }
    for(int i=0;i<n;i++)
        f[1<<i][i]=1;//初始化
    for(int S=1;S<=(1<<n)-1;S++){//枚举点集
        for(int i=0;i<n;i++){//刷表只能由自己转移到别人
            if(!f[S][i]) continue;//自己状态必须合法访问过
            int p=lowbit(S);//p为当前集合S位置最小的一点
            for(int j=p;j<n;j++){//访问比起点大的点作为下一点
                if(!Map[i][j]) continue;//必须与i连边
                if(S&(1<<j)){//j访问到当前点集
                    if(j==p)//j正好为起点出现了圈
                        ans+=f[S][i];//累加答案
                }
                else//状态转移
                    f[S|(1<<j)][j]+=f[S][i];
            }
        }
    }//输出答案
    printf("%lldn",(ans-m)/2ll);
    return 0;
}

最后

以上就是有魅力菠萝最近收集整理的关于A Simple Task(CodeForces-11D)(状压DP，剖析讲解)前言题目思路代码的全部内容，更多相关A内容请搜索靠谱客的其他文章。