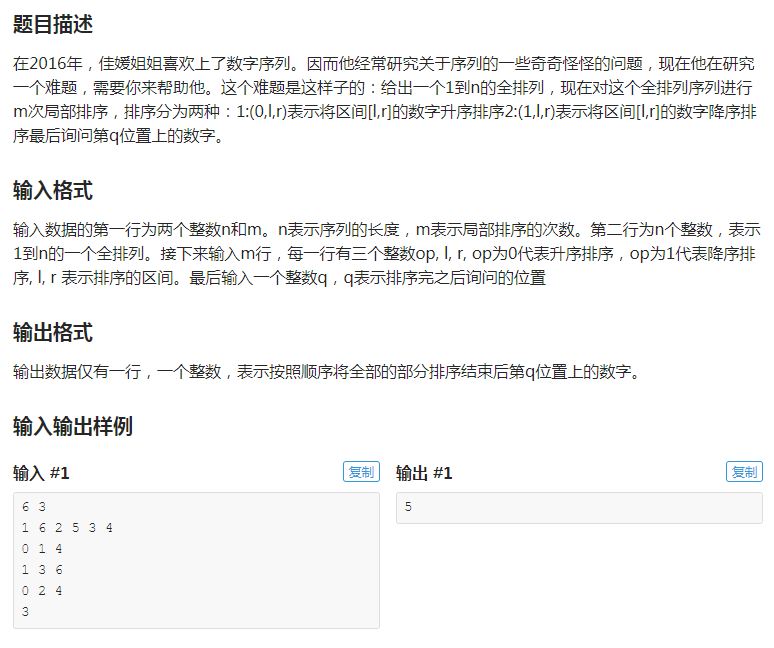
【题意分析】
首先，暴力sort有30pts…
全排列是一个特别好的性质，我们想想有没有特别的做法。
由于数字保证不重复，对于x，把大于等于x的数全部变为1，把小于x的数全部变成0。
那么我们可以发现：对于要排序的区间[l,r]，如果是升序，那么区间前面肯定是若干个零，后面全是1，如果是降序，那么区间前面全都是1， 后面全都是0。
然后这样操作之后我们看看要求的q位置上数字是否为1，就可以初步确定排完后这个位置上的数比x大还是比x小。（1是比x大，0是比x小）
想到什么？二分这个x，二分到最后无法再放缩时，说明我们已经找到了答案。
现在唯一的问题就是排序，由于序列全是0和1，我们可以考虑用线段树维护：利用线段树可以求出每段区间有几个0与几个1（区间求和就可以算出几个1），排序时，只要一段一段地赋值即可。
具体操作：对于区间
[
l
,
r
]
[l,r]
[l,r]有res个1，那么如果是降序，
[
l
,
l
+
r
e
s
−
1
]
[l,l+res-1]
[l,l+res−1]为1,
[
l
+
r
e
s
,
r
]
[l+res,r]
[l+res,r]为0.
如果是升序，
[
l
,
r
−
r
e
s
]
[l,r-res]
[l,r−res]为0，
[
r
−
r
e
s
+
1
,
r
]
[r-res+1,r]
[r−res+1,r]为1
Code :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95#include <iostream> #include <cstdio> #include <cstdlib> #include <cstring> #include <cctype> #include <algorithm> #define MAXN 200000 using namespace std; struct Node { int opt, l, r; }ques[MAXN]; int tree[MAXN << 2], lazy[MAXN << 2], a[MAXN], b[MAXN], n, q, res, pos, ans; inline int read () { register int s = 0, w = 1; register char ch = getchar (); while (! isdigit (ch)) {if (ch == '-') w = -1; ch = getchar ();} while (isdigit (ch)) {s = (s << 3) + (s << 1) + (ch ^ 48); ch = getchar ();} return s * w; } inline void pushup (int now) { tree[now] = tree[now << 1] + tree[now << 1 | 1]; } inline void pushdown (int now, int L, int R) { int mid = L + R >> 1; tree[now << 1] = lazy[now] * (mid - L + 1); tree[now << 1 | 1] = lazy[now] * (R - mid); lazy[now << 1] = lazy[now]; lazy[now << 1 | 1] = lazy[now]; lazy[now] = -1; } void build (int now, int l, int r) { lazy[now] = -1; if (l == r) {tree[now] = b[l]; return;} int mid = l + r >> 1; build (now << 1, l, mid); build (now << 1 | 1, mid + 1, r); pushup (now); } void update (int now, int l, int r, int L, int R, int k) { if (R < l || r < L) return; if (L <= l && r <= R) {tree[now] = (r - l + 1) * k, lazy[now] = k; return;} if (lazy[now] != -1) pushdown (now, l, r); int mid = l + r >> 1; update (now << 1, l, mid, L, R, k); update (now << 1 | 1, mid + 1, r, L, R, k); pushup (now); } void query (int now, int l, int r, int L, int R) { if (R < l || r < L) return; if (L <= l && r <= R) {res += tree[now]; return;} if (lazy[now] != -1) pushdown (now, l, r); int mid = l + r >> 1; query (now << 1, l, mid, L, R); query (now << 1 | 1, mid + 1, r, L, R); } inline bool check (int x) { for (register int i = 1; i <= n; i++) b[i] = (a[i] >= x); memset (tree, 0, sizeof tree), build (1, 1, n); query (1, 1, n, 1, 1); for (register int i = 1; i <= q; i++) { res = 0, query (1, 1, n, ques[i].l, ques[i].r); if (ques[i].opt == 0) { update (1, 1, n, ques[i].l, ques[i].r - res, 0); update (1, 1, n, ques[i].r - res + 1, ques[i].r, 1); } else { update (1, 1, n, ques[i].l, ques[i].l + res - 1, 1); update (1, 1, n, ques[i].l + res, ques[i].r, 0); } } res = 0, query (1, 1, n, pos, pos); return res; } int main () { n = read (), q = read (); for (register int i = 1; i <= n; i++) a[i] = read (); for (register int i = 1; i <= q; i++) ques[i].opt = read (), ques[i].l = read (), ques[i].r = read (); pos = read (); int L = 1, R = n; while (L <= R) { int mid = L + R >> 1; if (check (mid)) ans = mid, L = mid + 1; else R = mid - 1; } return printf ("%dn", ans), 0; }
最后
以上就是爱笑招牌最近收集整理的关于[TJOI2016]排序——[线段树]的全部内容，更多相关[TJOI2016]排序——[线段树]内容请搜索靠谱客的其他文章。
![[TJOI2016]排序——[线段树]](/uploads/reation/bcimg7.png)
发表评论 取消回复