VisualDL使用

VisualDL的代码仓地址是 https://github.com/PaddlePaddle/VisualDL/

这里摘录里面的一个scalar（折线图）例子

import random
from visualdl import LogWriter

logdir = "./tmp"
logger = LogWriter(logdir, sync_cycle=10000)

# mark the components with 'train' label.
with logger.mode("train"):
    # create a scalar component called 'scalars/scalar0'
    scalar0 = logger.scalar("scalars/scalar0")

# add some records during DL model running.
for step in range(100):
    scalar0.add_record(step, random.random())

保存为visual.py，运行后的结果，会生产一个tmp目录

$  tree .
.
├── tmp
│   ├── storage.meta
│   └── train%scalars%scalar0
└── visual.py

1 directory, 3 files

scalar0里面有很多打点信息，通过visualdl启动服务端，
$ visualdl --logdir=tmp --port=8080
浏览器打开 http://localhost:8080
就可以在看到

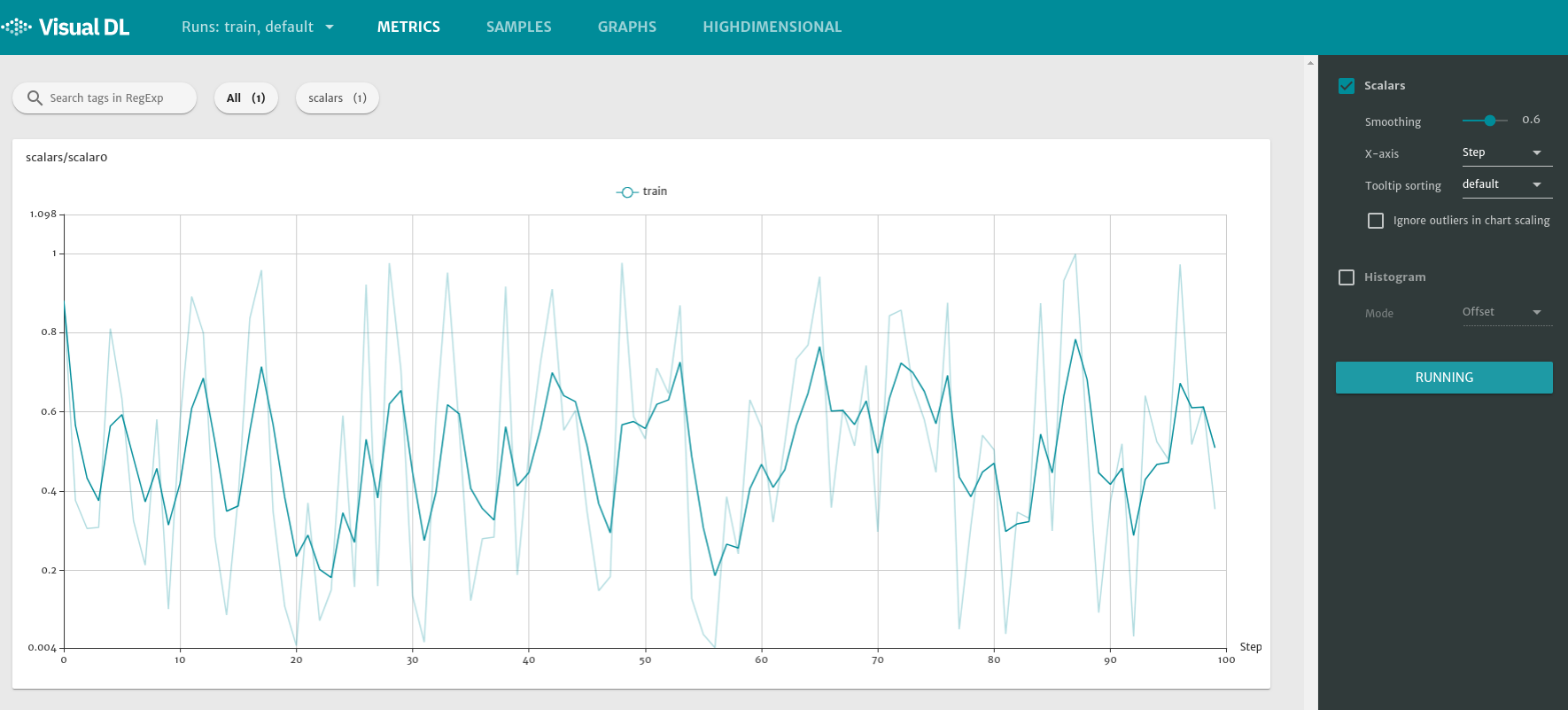
显示两条折线的问题

刚看的时候可能有点纳闷，为什么这里会有两条线？打点记录只有一种（也就是一个横坐标只有一个纵坐标），？原因就是因为右侧的Smoothing，smooth本身是为了提供平滑的功能，方便看出趋势

• 深色线：经过平滑处理的线
• 浅色线：原数据的线

如果我们把smoothing设置为0，这个时候两条线是重合的

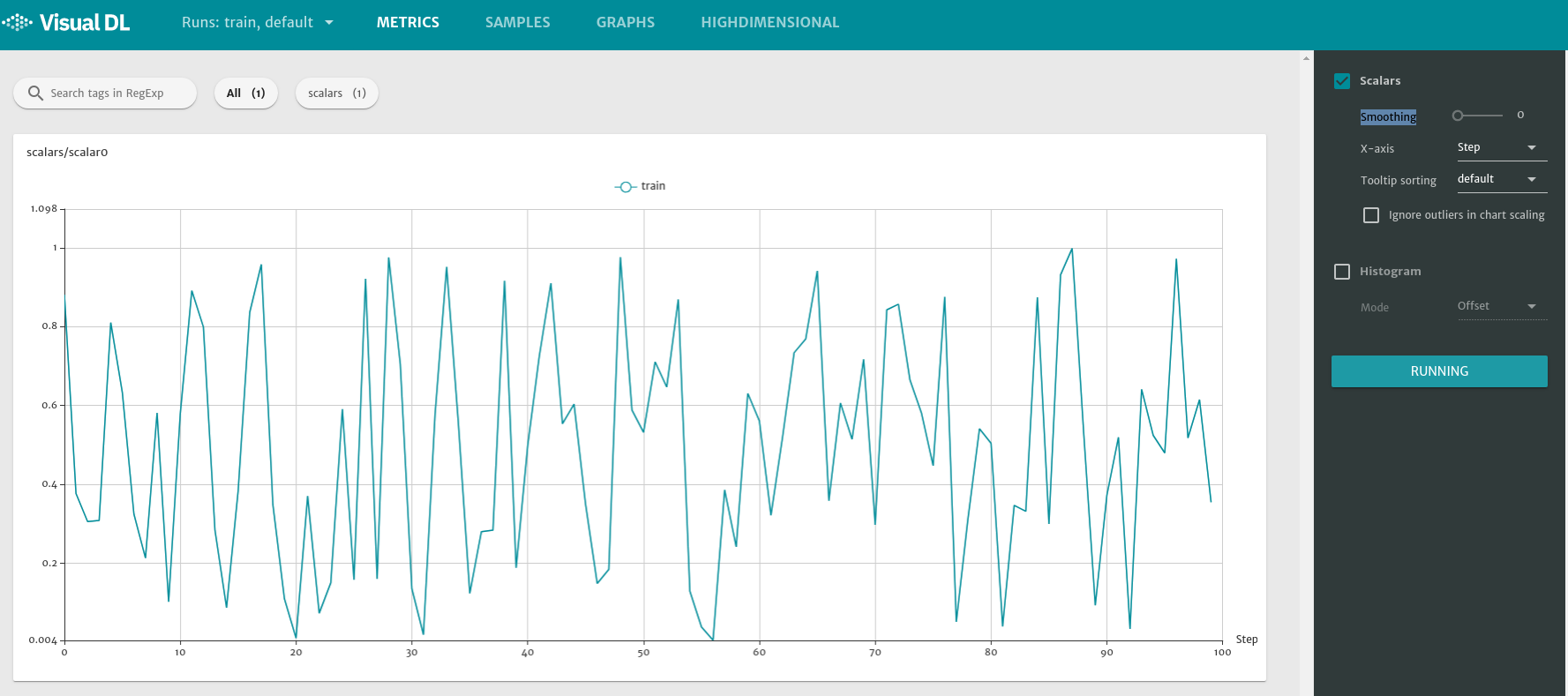
所以整个过程比较简单，在代码中打点，就可以看到对应的折线图

paddle 实现LR

原理的话，可以参考这篇文章，讲得比较清楚，包括sgd（随机梯度下降）的推导
https://mp.weixin.qq.com/s/7WlGN8JxfSmpJ8K_EyvgQA

这里主要讲代码实现
假设有一个线性函数：
$$y=2x_1+3x_2+1$$
需要提前预设一些值，
[[1.0,4.0],[2.0,5.0],[3.0,6.0],[4.0,7.0],[5.0,8.0]] 是[x1,x2]的一个列表
根据上述线性函数得出的对应结果
[[15.0],[20.0],[25.0],[30.0],[35.0]]
$$15=2\ast 1+3\ast 4+1$$
那么代码要实现的就是找到一组[w1,w2]以及bias值，使得误差最小。看到这，是不是感觉跟神经网络的fc层很像？

为了提高解的质量，加入了L2正则系数

import paddle.fluid as fluid
import numpy
from visualdl import LogWriter

logdir = "./tmp"
logger = LogWriter(logdir, sync_cycle=10000)

# mark the components with 'train' label.
with logger.mode("train"):
    # create a scalar component called 'scalars/scalar0'
    scalar0 = logger.scalar("scalars/scalar0")


# 定义输入数据
train_data=numpy.array([[1.0,4.0],[2.0,5.0],[3.0,6.0],[4.0,7.0],[5.0,8.0]]).astype('float32')
y_true = numpy.array([[15.0],[20.0],[25.0],[30.0],[35.0]]).astype('float32')

# 组建网络
x = fluid.data(name="x",shape=[None, 2],dtype='float32')
y = fluid.data(name="y",shape=[None, 1],dtype='float32')
y_predict = fluid.layers.fc(input=x,size=1,act=None)

# 定义损失函数
cost = fluid.layers.square_error_cost(input=y_predict,label=y)
avg_cost = fluid.layers.mean(cost)

# 选择优化方法
optimizer = fluid.optimizer.SGD(learning_rate=0.01,regularization=fluid.regularizer.L2Decay(0.005))

optimizer.minimize(avg_cost)

# 网络参数初始化
cpu = fluid.CPUPlace()
exe = fluid.Executor(cpu)
exe.run(fluid.default_startup_program())


# 开始训练，迭代100次
for i in range(100):
    y_predict_value, cost_value = exe.run(
        feed={'x':train_data, 'y':y_true},
        fetch_list=[y_predict, avg_cost])
    scalar0.add_record(i,cost_value.tolist()[0])


print("y_predict_value", y_predict_value)
print("cost_value", cost_value)

运行代码后的输出是，

y_predict_value [[14.992009]
 [19.994778]
 [24.997545]
 [30.000315]
 [35.003082]]
cost_value [2.1350283e-05]

y_predict_value基本接近预期，方差本身也很小了

启动visualdl服务端$ visualdl --logdir=tmp --port=8080
把smoothing设置为0，可以在浏览器看到

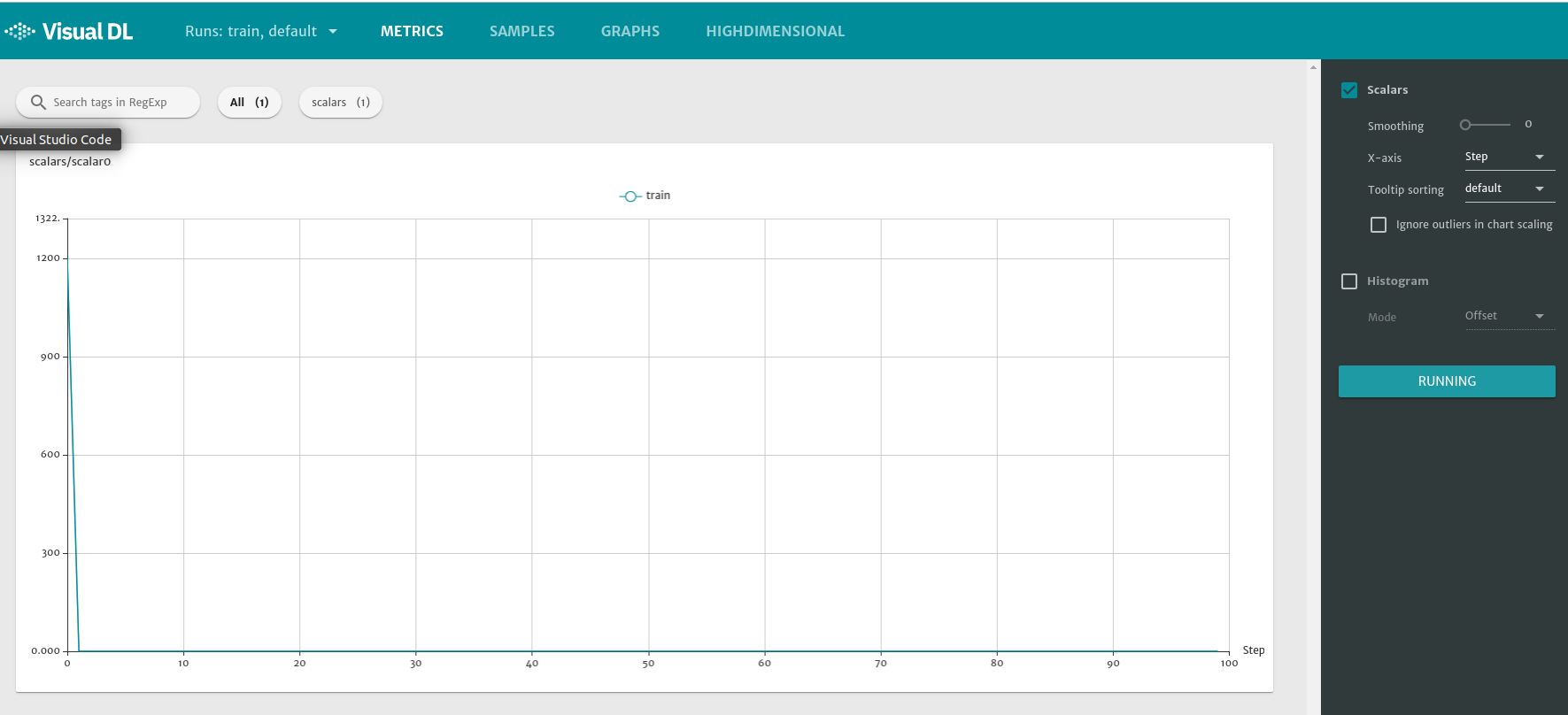
说明收敛效果还是很快的，5个step之后，解已经没有很大的改善了。
善于用visualdl，可以帮助我们更好观察训练过程

最后

以上就是活泼樱桃为你收集整理的paddle 线性回归LR以及VisualDL使用VisualDL使用paddle 实现LR的全部内容，希望文章能够帮你解决paddle 线性回归LR以及VisualDL使用VisualDL使用paddle 实现LR所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。