堆排序(Heap Sort):建堆,将最大值/最小值放到对应的位置上。
我们看堆排序以前,先回忆一下完全二叉树有一条性质,如果将一颗完全二叉树从0开始编号(从上到下,从左到右),结点编号i为0到n-1,如果满足2 i + 1 <= n - 1,则证明有左,满足2 i +2 <= n - 1,则证明有右,父亲结点的范围为0到 n / 2 - 1。那这与堆排序又有什么关系呢?堆的内部就是遵循以上逻辑关系的。注意:堆内部只是遵循完全二叉树所有的这条性质的逻辑关系,并非是一棵树,它的本质仍是数组。
待排数据为:8、12、19、1、14、7、20、6。这组数据并非是堆。我们先将这组数据按照逻辑结构化成二叉树的样子。
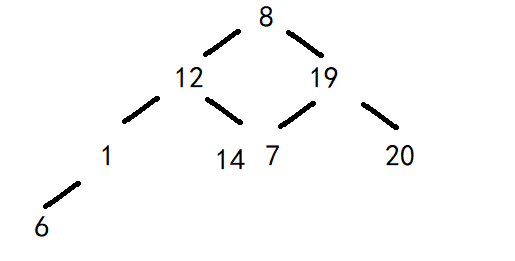
堆分为两种,大根堆(三者父亲最大):所有的父亲结点的值都大于其左右结点,小根堆(三者父亲最小)刚好反过来,所有根节点都小于其左右结点,并且不管是大根堆还是小根堆,左右兄弟结点是不存在比较关系的,只有父亲和孩子之间存在比较关系。
我们要先将堆建出来,建一个大堆。从最下面最后一个父亲结点1开始,6没有兄弟,1与左孩子6比,1比6小,二者交换。7与20比,20大,19与20比,20大,19与20交换,6与14比,14大,12与14比,14大,12与14交换,14与20比,20大,8与20比,20大,8与20交换,然后根的右结点已经调整过了,但是在调整完上面以后,他就不符合大堆的性质,需要再调,7和19比,19大,8和19比,19大,8与19交换。这时候大堆就算建完了为:20、14、19、6、12、7、8、1。
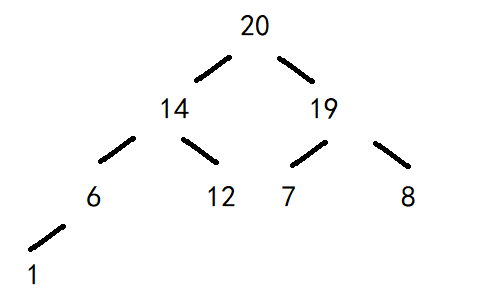
这时候大堆就算建完了为:20、14、19、6、12、7、8、1。
我们现在已经建完堆(初始堆)了,需要把最大/最小元素放到对应的位置上去,因为刚刚我们建的是大堆,所以堆顶一定是最大值。最大值要放在最后面,20与1交换,20没有必要在参与接下来的操作,剩余1、14、19、6、12、7、8。经过交换以后这已经不是大堆了,14与19比,19大,1与19比,19大,19与1交换,7和8比,8大,1和8,8大,1与8交换。
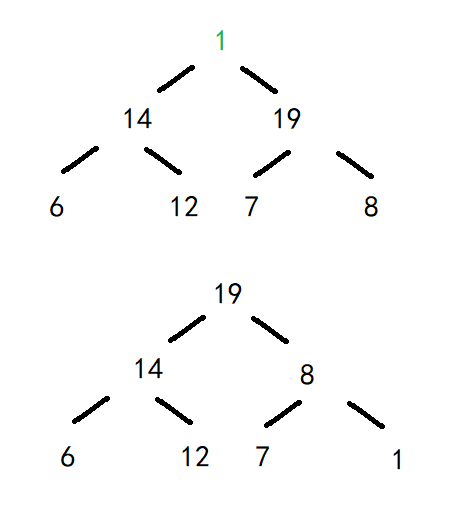
堆变成19、14、8、6、12、7、1。同理第二大元素19,19和1发生交换。剩余1、14、8、6、12、7;接着重复以上操作。
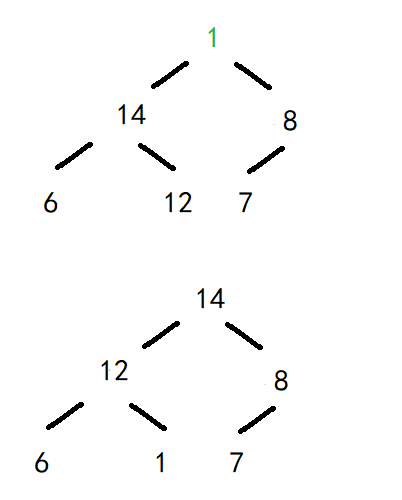
大堆为:14、12、8、6、1、7,第三大元素14,与倒数第三个元素发生交换,剩余7、12、8、6、1。
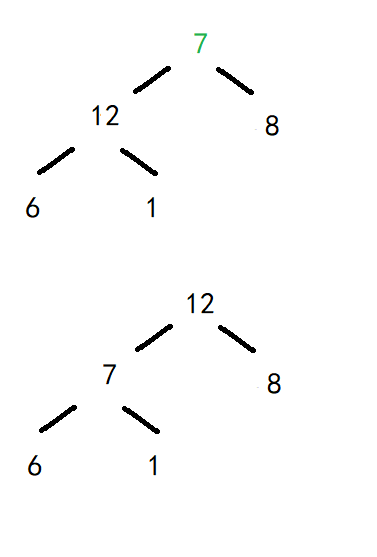
大堆为:12、7、8、6、1;第四大元素12,与倒数第4个元素交换;剩余1、7、8、6。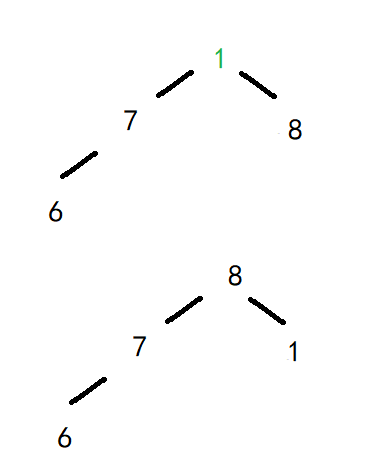
大堆为:8、7、1、6,第五大元素8与倒数第五个元素6发生交换;剩余6、7、1。
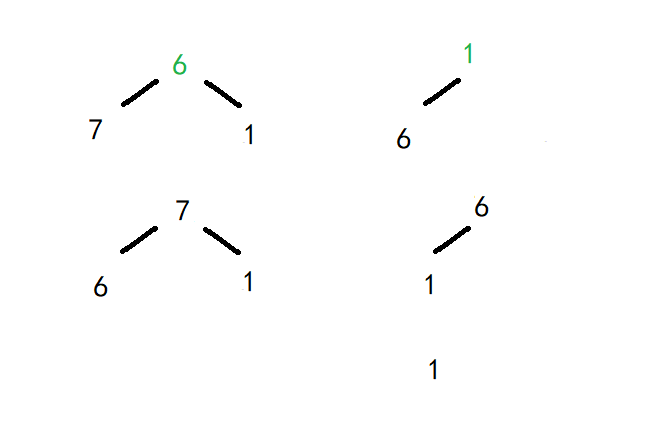
大堆为:7、6、1,堆顶7与当前最后操作元素1交换;剩余1、6。
大堆为:6、1,堆顶6与当前最后操作元素1交换;剩余1,结束。
排序完成:20、19、14、12、8、7、6、1。
#include<stdio.h>
#define LEFT (2*nRootID +1)
#define RIGHT (2*nRootID +2)
//堆排
void Adjust(int arr[],int nLength,int nRootID)
{
while(1)
{
//两个孩子
if(RIGHT < nLength)
{
//比较两个孩子大小
if(arr[LEFT] > arr[RIGHT])
{
//大的和父亲比较
if(arr[LEFT] > arr[nRootID])
{
arr[LEFT] = arr[LEFT]^arr[nRootID];
arr[nRootID] = arr[LEFT]^arr[nRootID];
arr[LEFT] = arr[LEFT]^arr[nRootID];
nRootID = LEFT;
continue;
}
else
{
break;
}
}
else
{
if(arr[RIGHT] > arr[nRootID])
{
arr[RIGHT] = arr[RIGHT]^arr[nRootID];
arr[nRootID] = arr[RIGHT]^arr[nRootID];
arr[RIGHT] = arr[RIGHT]^arr[nRootID];
nRootID = RIGHT;
continue;
}
else
{
break;
}
}
}
//一个孩子
else if(LEFT < nLength)
{
if(arr[LEFT] > arr[nRootID])
{
arr[LEFT] = arr[LEFT]^arr[nRootID];
arr[nRootID] = arr[LEFT]^arr[nRootID];
arr[LEFT] = arr[LEFT]^arr[nRootID];
nRootID = LEFT;
continue;
}
else
{
break;
}
}
//0个孩子
else
{
break;
}
}
}
void HeapSort(int arr[],int nLength)
{
if(arr == NULL || nLength <=0) return;
//创建初始堆
int i;
for(i = nLength/2-1;i >= 0;i--)
{
//调整各个父亲结点
Adjust(arr,nLength,i);
}
for(i = nLength-1;i > 0;i--)
{
//交换
arr[i] = arr[i]^arr[0];
arr[0] = arr[i]^arr[0];
arr[i] = arr[i]^arr[0];
//调整堆顶
Adjust(arr,i,0);
}
}
void Printf(int arr[],int nlength)
{
if(arr == NULL || nlength <= 0) return;
int i;
for(i = 0;i < nlength;i++)
{
printf("%d ",arr[i]);
}
}
int main()
{
int arr[] = {10,2,11,4,56};
HeapSort(arr,sizeof(arr)/sizeof(arr[0]));
Printf(arr,sizeof(arr)/sizeof(arr[0]));
printf("n");
return 0;
}
堆排优化:
调整的三段代码都是孩子里大的与父亲进行比较,然后如果较大的孩子比父亲大,二者就发生交换。那我们一开始来的时候就找到较大的孩子赋值给MAX,接下来让MAX与父亲进行比较。
void Adjust2(int arr[],int nLength,int nRootID)
{
int MAX;
for(MAX = LEFT;MAX < nLength;MAX = LEFT)
{
//有两个孩子
if(RIGHT < nLength)
{
if(arr[MAX]<arr[RIGHT])
{
MAX = RIGHT;
}
}
//大的和父亲比较
if(arr[MAX] > arr[nRootID])
{
arr[MAX] = arr[MAX]^arr[nRootID];
arr[nRootID] = arr[MAX]^arr[nRootID];
arr[MAX] = arr[MAX]^arr[nRootID];
nRootID = MAX;
}
else
{
break;
}
}
}
最后
以上就是野性金鱼最近收集整理的关于经典排序之堆排序及其优化的全部内容,更多相关经典排序之堆排序及其优化内容请搜索靠谱客的其他文章。








发表评论 取消回复