一、分类
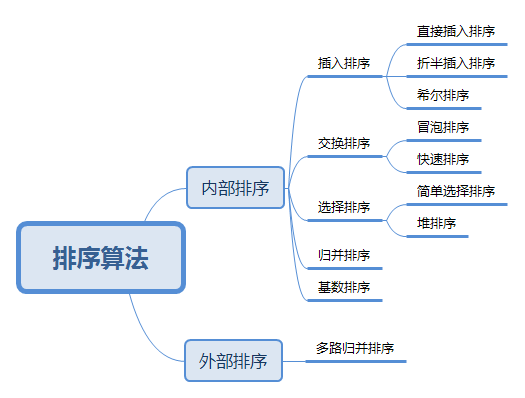
二、实现
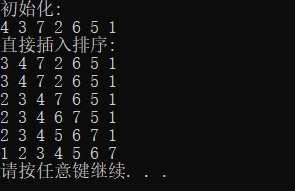
1.直接插入排序
//无哨兵,0号单元存储实际值
void StraightInsertSort(int A[], int n) //n是元素个数
{
int i, j, tmp;
for (i = 1; i < n; i++) //依次将A[1]~A[n-1]插入到前面已排序序列
{
if (A[i - 1] > A[i]) //比较前驱元素和当前元素大小,判断是否需要插入
{
tmp = A[i]; //待插入的值放到tmp暂存
for (j = i - 1; tmp < A[j]; --j) //从后往前查找待插入位置
{
A[j + 1] = A[j]; //元素向右移动
}
A[j + 1] = tmp; //复制到插入位置
}
}
}
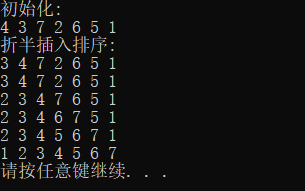
2.折半插入排序
//无哨兵,0号单元存储实际值
void BinaryInsertSort(int A[], int n) //n是元素个数
{
int i, j, low, high, mid, tmp;
for (i = 1; i < n; i++) //依次将A[1]~A[n-1]插入到前面已排序序列
{
tmp = A[i]; //待插入的值放到tmp暂存
low = 0;
high = i - 1; //设置折半查找的范围
while (low <= high) //折半查找
{
mid = (low + high) / 2; //取中间点(向左取整)
if (A[mid] > tmp)
high = mid - 1; //查找左半子表
else
low = mid + 1; //查找右半子表
}
for (j = i - 1; j >= high + 1; j--) //high+1 为插入位置
{
A[j + 1] = A[j];
}
A[high + 1] = tmp; //将值插入
}
}
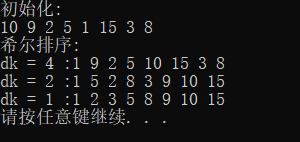
3.希尔排序
//无哨兵,0号单元存储实际值
void ShellSort(int A[], int n) //n是元素个数
{
int i, j, tmp, dk;
for (dk = n / 2; dk >= 1; dk = dk / 2) //位置增量值
{
for (i = dk; i < n; i++) //依次将A[1]~A[n-1]插入到前面已排序序列
{
if (A[i - dk] > A[i]) //比较前驱元素和当前元素大小,判断是否需要插入
{
tmp = A[i]; //待插入的值放到tmp暂存
for (j = i - dk; j >= 0 && tmp < A[j]; j -= dk) //从后往前查找待插入位置
{
A[j + dk] = A[j]; //元素向右移动
}
A[j + dk] = tmp; //复制到插入位置
}
}
}
}
4.冒泡排序
void BubbleSort(int A[], int n) //n是元素个数
{
bool flag;
int i, j, tmp;
for (i = 0; i < n - 1; i++) //循环n-1趟
{
flag = false; //表示本趟冒泡是否发生交换的标志
for (j = n - 1; j > i; j--) //每趟循环的次数,从后向前找最小,升序排序
{
if (A[j - 1] > A[j]) //交换
{
tmp = A[j - 1];
A[j - 1] = A[j];
A[j] = tmp;
flag = true;
}
}
if (flag == false) //本趟遍历没有发生交换说明已经有序
return;
}
}
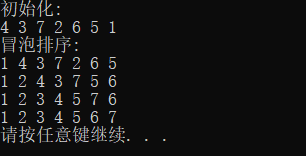
5.快速排序
int Partition(int A[], int low, int high) //划分操作
{
int pivot = A[low]; //将当前表中第一个元素设为枢轴值,对表进行划分
while (low < high)
{
while (low < high && A[high] >= pivot)
high--;
A[low] = A[high]; //将比枢轴值小的元素移动到左端
while (low < high && A[low] <= pivot)
low++;
A[high] = A[low]; //将比枢轴值大的元素移动到右端
}
A[low] = pivot; //枢轴元素放到最终位置
return low; //返回最终位置
}
void QuickSort(int A[], int low, int high)
{
int pivotpos;
if (low < high) //递归跳出条件
{
pivotpos = Partition(A, low, high); //划分为两个子表
QuickSort(A, low, pivotpos - 1); //对子表递归排序
QuickSort(A, pivotpos + 1, high);
}
}
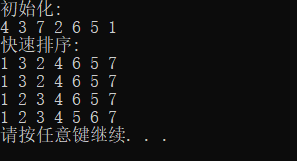
6.简单选择排序
void SelectSort(int A[], int n) //n是元素个数
{
int i, j, min, tmp;
for (i = 0; i < n - 1; i++) //循环n-1趟
{
min = i; //min记录最小元素位置
for (j = i + 1; j < n; j++) //在A[i~n-1]中选择最小元素
if (A[j] < A[min])
min = j; //更新最小元素位置
if (min != j) //交换
{
tmp = A[i];
A[i] = A[min];
A[min] = tmp;
}
}
}
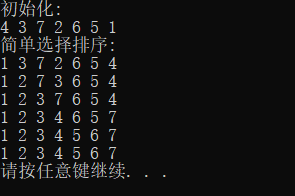
7.堆排序
A[0]用于暂存,不存储实际数据
- 小根堆:L(i) <= L(2*i)且L(i) <= L(2*i+1)
- 大根堆:L(i) >= L(2*i)且L(i) >= L(2*i+1) (1<=i<=⌊n/2⌋)
void AdjustDown(int A[], int k, int len) //将元素k向下进行调整
{
int i;
A[0] = A[k]; //A[0]用于暂存
for (i = 2 * k; i <= len; i *= 2) //沿k较大的子结点向下筛选
{
if (i < len && A[i] < A[i + 1])
i++; //取k较大的子结点的下标
if (A[0] >= A[i]) //筛选结束
break;
else
{
A[k] = A[i]; //将A[i]调整到双亲结点上
k = i; //修改k值以便继续向下筛选
}
}
A[k] = A[0]; //被筛选的节点的值放入最终位置
}
void BuildMaxHeap(int A[], int len) //建立大根堆
{
int i;
for (i = len / 2; i > 0; i--)
{
AdjustDown(A, i, len);
}
}
void HeapSort(int A[], int len)
{
int i, tmp;
BuildMaxHeap(A, len); //初始建堆
for (i = len; i > 1; i--) //n-1趟的交换和建堆过程
{
tmp = A[i]; //交换
A[i] = A[1];
A[1] = tmp;
AdjustDown(A, 1, i - 1);//把剩余的i-1个元素整理成堆
}
}
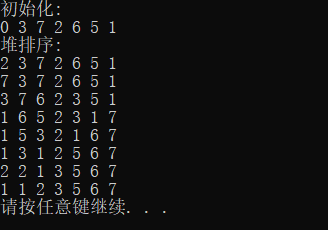
8.归并排序
int *B = (int *)malloc(n * sizeof(int)); //辅助数组B
void Merge(int A[], int low, int mid, int high) //将前后相邻的两个有序表归并为一个有序表
{
int i, j, k;
for (k = low; k <= high; k++)
{
B[k] = A[k]; //将A中所有元素复制到B中
}
for (i = low, j = mid + 1, k = i; i <= mid && j <= high; k++)
{
if (B[i] <= B[j]) //比较B的左右两段中的元素
A[k] = B[i++]; //将较小的值放到A中
else
A[k] = B[j++];
}
while (i <= mid) //若第一个表未检测完
A[k++] = B[i++]; //复制剩余元素到A中
while (j <= high) //若第二个表未检测完
A[k++] = B[j++]; //复制剩余元素到A中
}
void MergeSort(int A[], int low, int high)
{
int mid;
if (low < high)
{
mid = (low + high) / 2; //从中间划分两个子序列
MergeSort(A, low, mid); //对左侧子序列进行递归排序
MergeSort(A, mid + 1, high);//对右侧子序列进行递归排序
Merge(A, low, mid, high); //归并
}
}
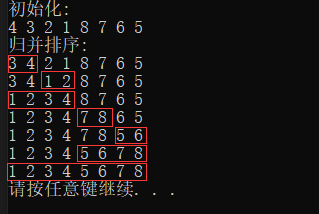
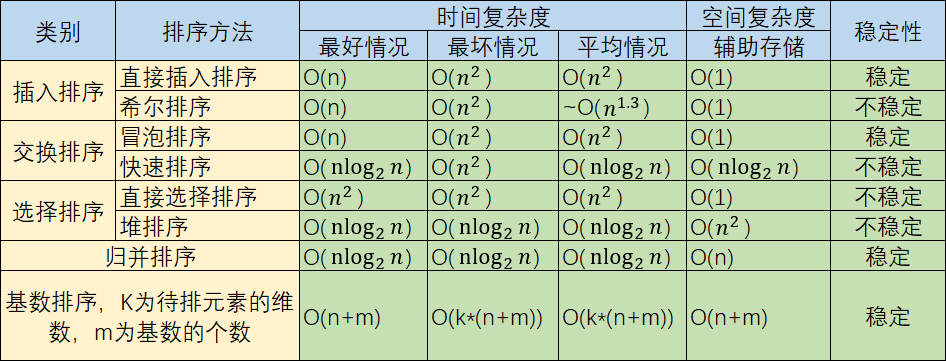
三、性能分析
最后
以上就是纯情小懒虫最近收集整理的关于排序算法-C语言实现的全部内容,更多相关排序算法-C语言实现内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复