（C语言）七大常见排序算法之 详解版 -＞（希尔 快排 冒泡 归并排等）

                                                把优秀当成一种习惯。

本文章将带大家了解常见的排序算法都有哪些，以及都是怎么实现的。

排序一共可以分为四大类：

---

 

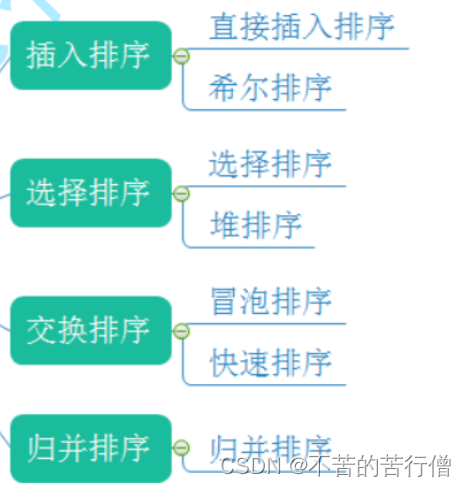
一.直接插入排序及其代码的实现

 

老规矩先来了解下概念

比如以下的一个题目，请你先自我思考这个代码是你，你要如何实现呢？

把一个数组 5 2 4 6 1 3排序成升序的数组。

 

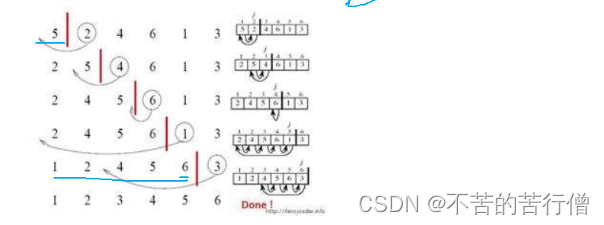
思路：通过图我们能发现，插入排序第一趟是把前一个数当成有序的，要插入数据时候，是把后一个往前K个有序序列中插入。以此类推 

好了 接下来直接上代码

//测试插入排序
void TestInsertSort()
{
	int a[] = { 4, 3, 7, 1, 9, 8, 4, 3, 5 };
	InsertSort(a, sizeof(a) / sizeof(int));
	PrintArray(a, sizeof(a) / sizeof(int));
}

//插入排序代码的实现
void InsertSort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		//把tmp插入到数组的【0，end】的有序区间中
		//要比较的位置
		int end = i;
		//记录要插入的数 因为比较后可能会把end往后移到end+1的位置 所以要先保存end+1位置的数据下来
		int tmp = a[end + 1];
		while (end >= 0)
		{
			//从end位置开始比较，大就把end的数往后移动 继续跟end前一个比较
			//直到对比到合适的位置
			if (a[end] > tmp)
			{
				a[end + 1] = a[end];
                //从end往前比较
				end--;
			}
			//说明碰到比tmp要小的数 
			else
				break;
		}
		//该语句是0-end区间都没有比tmp大的数，以及找到了比tmp小的数
		//插入都是往end+1的位置插入
		a[end + 1] = tmp;
	}
}

 

了解完插入排序的实现以后，那么它的时间复杂度以及空间复杂度分别为多少呢？

我们要对n个数进行n趟排序，最坏的情况下要遍历到最开头的位置。

最好的情况就是有序，该情况为O（n） 接近有序我们也可以认为是O(n)  因为有几个数不是有序的无非就是 O（n+x）而已  这个X是一个很小的常数，可以忽略不计。

所以该算法的空间复杂度为：

 

---

 

 二.希尔排序及其算法的实现

 

既然我们学排序算法，那么肯定是不会选择时间复杂度以及空间复杂度都很高的算法。上面我们所学习的插入排序的时间复杂度为O（n²) 也就是说如果我们的数据有100W个，那么用插入排序的算法要算100W*100W次=1万亿次  我们现在的计算机运行速度已经很快了，一秒可以达到上亿次，而用插入排序，计算机要运行的时间要十几秒钟，所以效率是非常低的，因为希尔就在插入排序的算法上进行了优化，因此成为希尔排序算法。

 

希尔算法又可以分为两步走：

1.预排序 （让数据接近有序）  把数据分为gap组，每组间隔为gap（gap>1时 是为第二步做铺垫）

2.直接插入排序  （当gap间隔为1时 相当于直接插入排序）

 

 

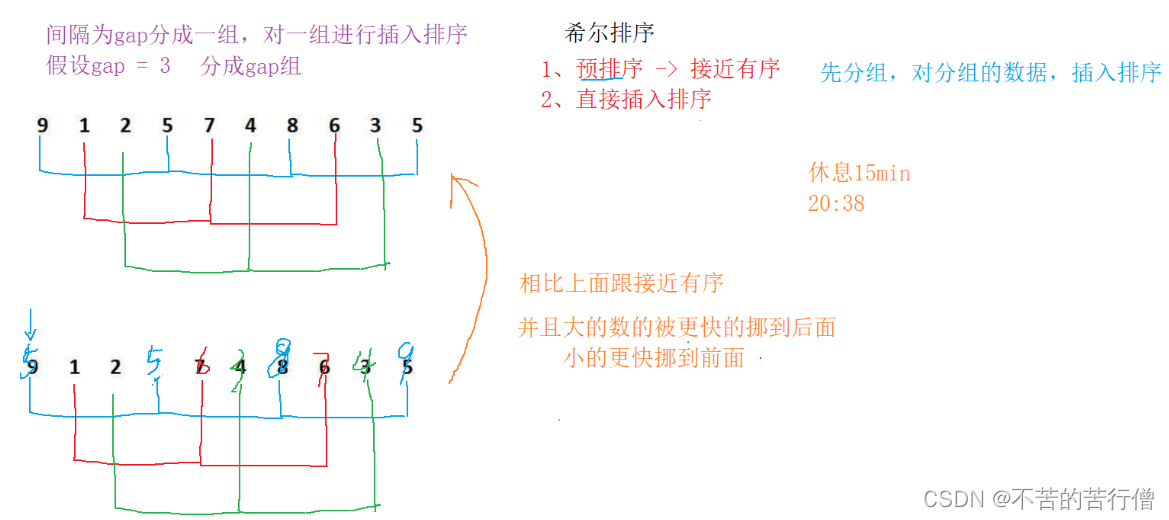
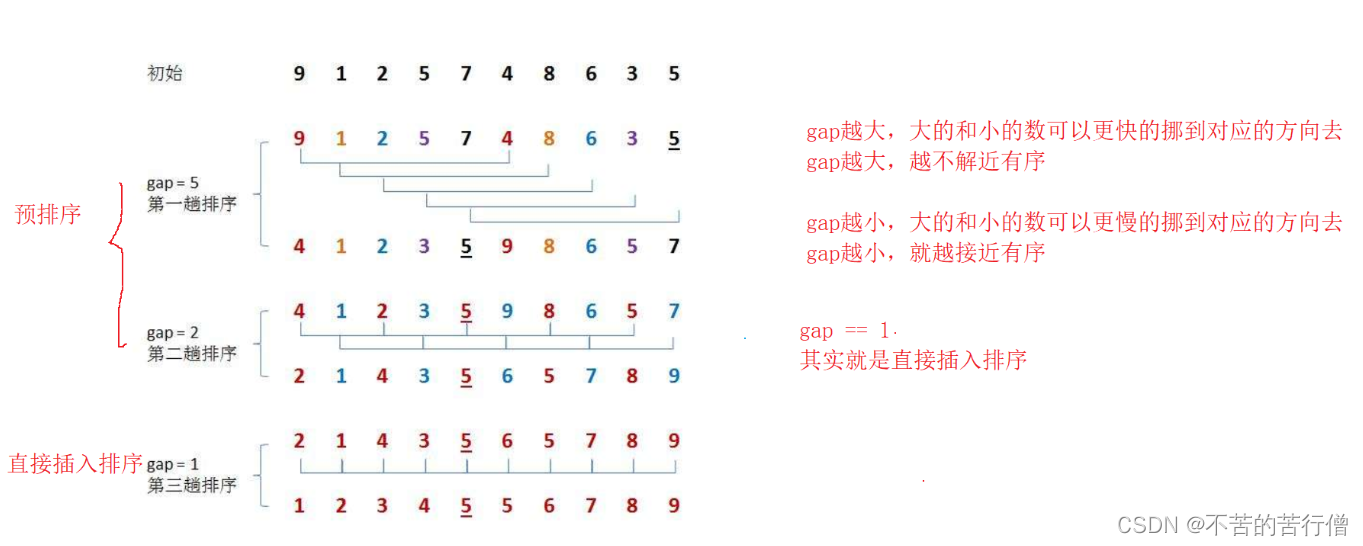
 我们直接上代码来感受

//测试希尔排序
void TestShellSort()
{
	int a[] = { 10,9,8,7,6,5,4,3,2,1,-1,-2,-3,-4,-5,-6,-7,-8,-9,-10,-11 };

	ShellSort(a, sizeof(a) / sizeof(int));
	PrintArray(a, sizeof(a) / sizeof(int));
}

//希尔排序代码实现
void ShellSort(int* a, int n)
{
	int gap = n;
    
	while (gap > 1)
	{
		//gap进行预排序
        //gap除以几都可以，只是说除以3是最好的选择
		gap = (gap / 3) + 1;//防止gap为0的情况，如果为0则相当于没有排序，所以在后面多加了个1，gap=1相当于插入排序
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

---

 

 

三.比较希尔排序跟直接插入排序

 

void TestOP()
{
    //生成随机数
	srand(time(0));
	const int N = 100000;
    //创建6个10W的数组
	int* a1 = (int*)malloc(sizeof(int)*N);
	int* a2 = (int*)malloc(sizeof(int)*N);
	int* a3 = (int*)malloc(sizeof(int)*N);
	int* a4 = (int*)malloc(sizeof(int)*N);
	int* a5 = (int*)malloc(sizeof(int)*N);
	int* a6 = (int*)malloc(sizeof(int)*N);
    
     //往里面存入数据
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];

	}

    //记录起始的时间跟结束的时间
	int begin1 = clock();
	InsertSort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	//int begin3 = clock();
	//SelectSort(a3, N);
	//int end3 = clock();

	//int begin4 = clock();
	//HeapSort(a4, N);
	//int end4 = clock();

	//int begin5 = clock();
	//QuickSort(a5, 0, N - 1);
	//int end5 = clock();

	//int begin6 = clock();
	//MergeSort(a6, N);
	//int end6 = clock();

    //用结束的时间减去起始的时间得到运行的时间
	printf("InsertSort:%dn", end1 - begin1);
	printf("ShellSort:%dn", end2 - begin2);
	//printf("SelectSort:%dn", end3 - begin3);
	//printf("HeapSort:%dn", end4 - begin4);
	//printf("QuickSort:%dn", end5 - begin5);
	//printf("MergeSort:%dn", end6 - begin6);


    //释放开辟的六个数组
	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
}

 

注意：clock（）函数记录的时间是毫秒 所以直接插入排序的时间12063为12.063秒   希尔排序为0.025秒    所以同样的数据，处理的效率的差距是很大的。

---

 

总结：插入排序法 > 冒泡排序法 > 选择排序

---

 

四.选择排序（最差的排序算法）

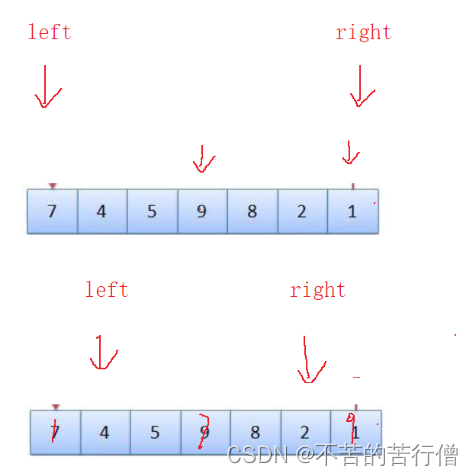
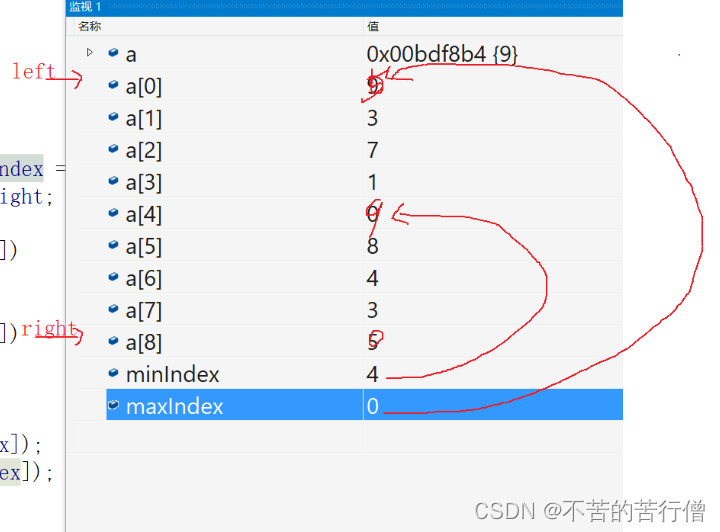
思路：在 left - right 区间 先遍历 找出最大值跟最小值  然后分别放到第一位跟最后一位 （mid跟left的数据互关，然后max跟right位置的数据互关） 然后left++   right-- 缩小区间  再在left - right 区间找出次小的数  以此类推

最后得到一个有序数组

 

left 跟 right 都是从最左边left位置开始找向右查找 因为这样才能够保证扫描到每个数据，不让right从右边开始扫描的原因是因为会改变right的下标 不方便把最大值放到最右边了

找到最大最小后  次大次小的数就在 【left+1  right-1 】的区间进行查找 同样的记录最大值最小值的下表还是从最左边开始 这时候最左边的下标位 left+1

 

 

//测试选择排序
void TestSelectSort()
{
	//int a[] = { 9, 3, 7, 1, 0, 8, 4, 3, 5 };
	//int a[] = {11,9, 4, 3, 7, 1, 9, 8, 4, 3, 5, 0, 1, 3};
	int a[] = { 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, -1, -2, -3, -4, -5, -6, -7, -8, -9, -10, -11 };

	SelectSort(a, sizeof(a) / sizeof(int));
	PrintArray(a, sizeof(a) / sizeof(int));
}

// N N-2 N-4...
// O(N^2)
//选择排序
void SelectSort(int* a, int n)
{
	int left = 0, right = n - 1;
	while (left < right)
	{
		// 初始时让最大跟最小都为第一个
		int minIndex = left, maxIndex = left;
		for (int i = left; i <= right; ++i)
		{
			//记录最小值的下标
			if (a[i] < a[minIndex])
				minIndex = i;
			//记录最大值的下标
			if (a[i] >= a[maxIndex])
				maxIndex = i;
		}
		//找到left-right区间里最小值跟最大值 交换
		Swap(&a[left], &a[minIndex]);
		// 如果max和left位置重叠，max被换走了，要修正一下max的位置
		if (left == maxIndex)
			maxIndex = minIndex;

		Swap(&a[right], &a[maxIndex]);
		//缩小left - right的区间  再找出次小跟次大的值
		++left;
		--right;
	}
}

---

快排分为三种版本：1.hoare版本（左右指针法）  2.挖坑法                      3.前后指针法

---

 

五.快速排序 - > hoare版本（左右指针法）

左边的都比key小 右边的都比key大

因为该算法需要用到递归 所以先来了解下单趟排序

 

 

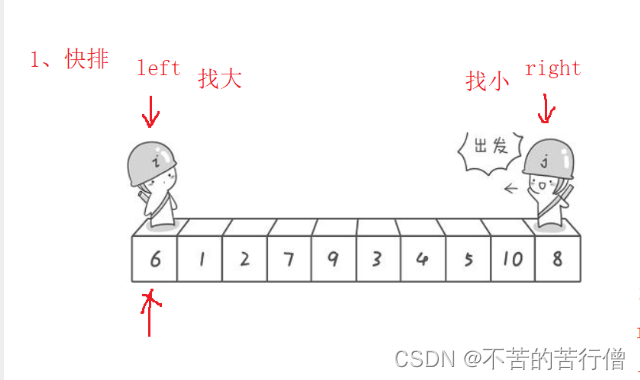
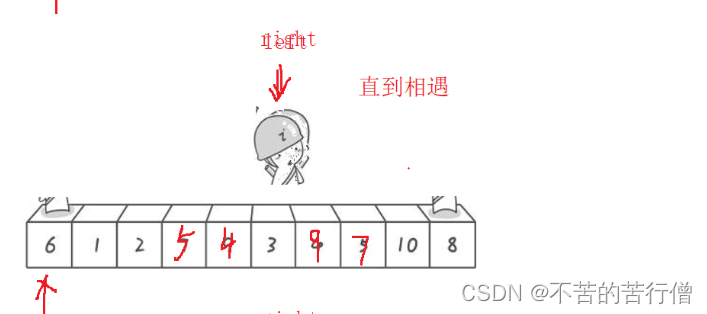
最后一步：相遇以后 把key 跟相遇的位置的值交换（key在二分的位置为最理想的情况），那么一趟快排就算完成了

 

直接上代码感受下

void QuickSort(int* a, int begin, int end)
{

	//left从左往右找打   right从右往左找小
	int left = begin, right = end;
	int key = left;
	//左小于右说明 一趟还没有结束
	while (left < right)
	{
		//定义的key在左边那就要右边的指向先动 在让左边的动
		//找小
		while (left < right && a[right] >= a[key])
		{
			--right;
		}
		//找大
		while (left < right && a[left] <= a[key])
		{
			++left;
		}
        
        //找到一大一小 交换  再继续向前找
		Swap(&a[left], &a[right]);
	}
    
    //记录下相遇位置的下标
	int meet = left;
	Swap(&a[key],&a[meet]);

}

 

注意：单趟排序好了以后 现在 key就换到了该换到的位置了，而且key的左边都是比key小的数 右边都是比key要大的数，接下来就要用到递归，把左边跟右边再进行排序。 我们只需要在上面的代码里加上递归就可以。

 

 

完整代码：

//快排 hoare版本 -- 左右指针法
void QuickSort(int* a, int begin, int end)
{

	//int a[] = { 11, 9, 4, 3, 7, 1, 9, 8, 4, 3, 5, 0, 1, 3 };
	if (begin >= end)
	{
		return;
	}
	//left从左往右找打   right从右往左找小
	int left = begin, right = end;
	int key = left;
	//左小于右说明 一趟还没有结束
	while (left < right)
	{
		//定义的key在左边那就要右边的指向先动 在让左边的动
		//找小
		while (left < right && a[right] >= a[key])
		{
			--right;
		}
		//找大
		while (left < right && a[left] <= a[key])
		{
			++left;
		}

		Swap(&a[left], &a[right]);
	}
    
    //记录下相遇的下标，该下标就是key本应该放置的位置
   //每一趟都会把key放到它本应该在的地方 并且左边都会比key小 右边都会比key大
	int meet = left;
	Swap(&a[key],&a[meet]);


    //递归左边
	QuickSort(a, begin, meet - 1);
    //递归右边    有点类似于二叉树的递归
	QuickSort(a, meet+1 ,end);


}

 分析完了快排的整套代码，那么我们接下来再对快排的效率进行一个分析

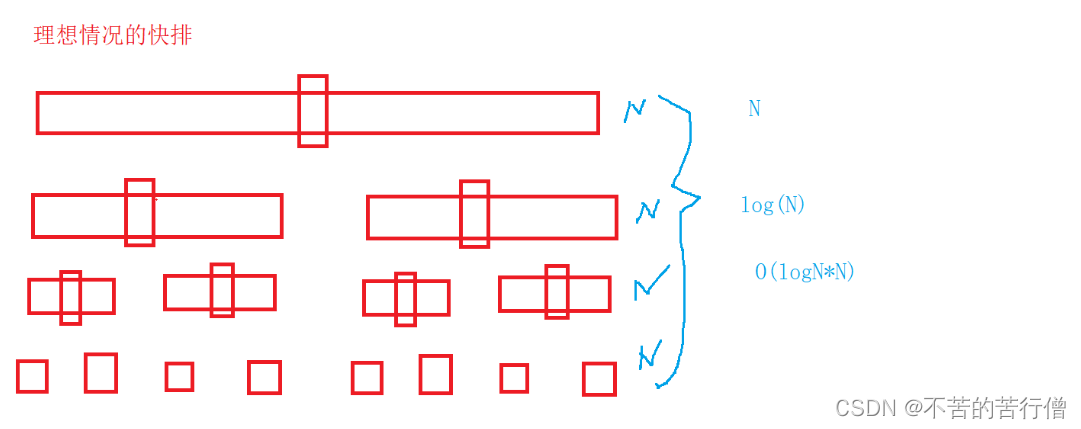
情况一：理想情况

快排最理想的情况就是每一趟的 key都处在整个数组的中间的位置（二分）

每一趟都会把数组分为左右 然后进行递归

递归到最后 画出来的图形会发现类似于我们所学的满二叉树  所以快排的时间复杂度为O（logN）

 

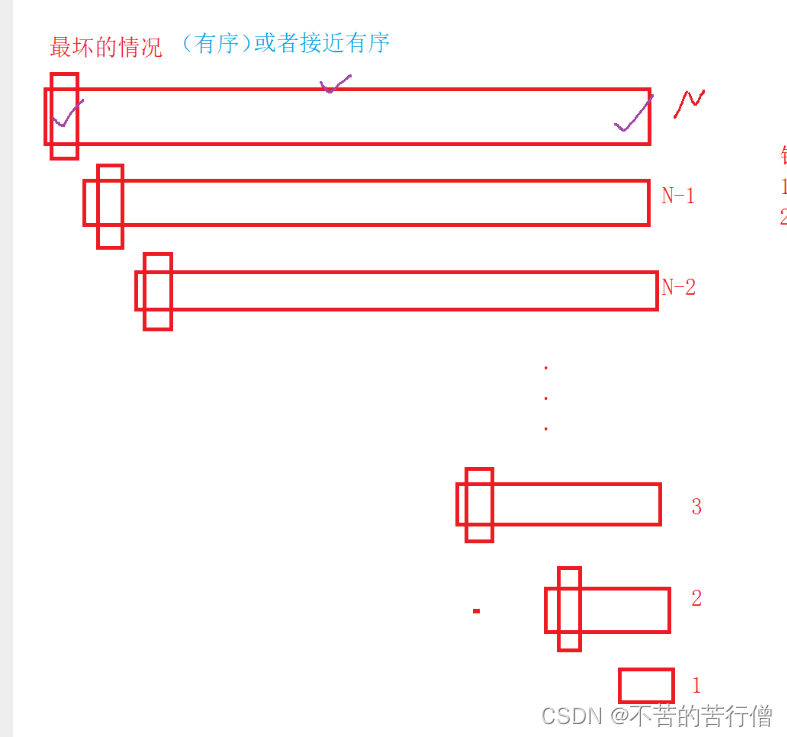
情况二：最坏的情况

如果要排的数组就是有序或者是接近有序的 那么这时候快排的效率就退化到了 O（N*N）

比如：9 8 7 6 5 4 3 2 1 

key = left = 9     right找大会发现从右往左找 一直到不到比9大的 直到找到0的位置  如果数组长度为N  那么right走一遍是N  N个数走N遍  就是N*N

        1 2 3 4 5 6 7 8 9

left从左往右找小 也一样的逻辑

问题：所以我们会发现 快排居然也有很慢的时候     

那么 我们应该怎么解决呢？   这里我们有两种办法对快排进行优化  可以防止排序的时候出现最坏的那种情况。 即三数取中 小区间优化（这两种方式可以整合到一起使用)

 

快排优化方式一：三数取中（本质是防止最坏的情况出现，即有序的时候）

 

我们取key 一般取最左边（left） 中间（min） 右边（right）

思路：我们为了防止出现有序的情况，就会采取取中间值的数值  即 a[left]  a[min]  a[rright] 这三个数中第二大的数（三个数的中间数）作为 key

 

直接上代码感受：

//快排优化：三数取中

//返回值就是中间的数 也就是我们选出来的key  
int GetMidIndex(int* a, int left, int right)
{
    //  ‘/’除号效率太低 所以我们选择用 右移符号来进行除以2  二进制右移一位相当于÷2
    //算出中间数的下标
	int mid = (left + right) >> 1;

	// left  mid  right
    
    //三个数比较 选出第二大的当key
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if (a[left] > a[right])
		{
			return left;
		}
		else
		{
			return right;
		} 
	}
	else // a[left] > a[mid]
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[left] < a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}

 

那么把三数取中往 代码里整合 

midIndex的值为三数取中的值   把该值跟begin的值互换，又回到了上面我们所讲的代码中了  只是这时候的begin是一个优化过后选取的begin。

//快排 hoare版本 -- 左右指针法
void QuickSort1(int* a, int begin, int end)
{

	//int a[] = { 11, 9, 4, 3, 7, 1, 9, 8, 4, 3, 5, 0, 1, 3 };
    //对最底层的递归进行一个判断处理
	if (begin >= end)
	{
		return;
	}
    
    //GetMidIndex函数返回的就是要作为key的值  用midIndex接收函数返回的中间值后 把原本最左边作为key的数a[begin]  跟a[midIndex]交换  然后接下来的步骤跟前面的代码完全相同了
   
	int midIndex = GetMidIndex(a, begin, end);
	Swap(&a[begin], &a[midIndex]);

	//left从左往右找打   right从右往左找小
	int left = begin, right = end;
	int key = left;
	//左小于右说明 一趟还没有结束
	while (left < right)
	{
		//定义的key在左边那就要右边的指向先动 在让左边的动
		//找小
		while (left < right && a[right] >= a[key])
		{
			--right;
		}
		//找大
		while (left < right && a[left] <= a[key])
		{
			++left;
		}

		Swap(&a[left], &a[right]);
	}

	//记录下相遇的下标，该下标就是key本应该放置的位置
   //每一趟都会把key放到它本应该在的地方 并且左边都会比key小 右边都会比key大
	int meet = left;
	Swap(&a[key], &a[meet]);


	//递归左边
	QuickSort1(a, begin, meet - 1);
	//递归右边    有点类似于二叉树的递归
	QuickSort1(a, meet + 1, end);


}

---

 

//前后指针
void QuickSort3(int* a, int begin, int end)
{
    //对递归进行判断
	if (begin >= end)
	{
		return;
	}
	//三数取中
	int midIndex = GetMidIndex(a, begin, end);
	Swap(&a[begin], &a[midIndex]);

	int prev = begin, cur = begin + 1;
	//要记录下标  不能新建一个变量把a[begin]的值存起来 因为这样改变不了数组
	int keyi = begin;
	while (cur <= end)
	{
		//找小 （写法不唯一）
		if (a[cur] < a[keyi] && ++prev != cur) //先判断两个的值相不相等 再判断++prev 跟 cur等不等
		{
			Swap(&a[cur], &a[prev]);
		}
		//++prev == cur 说明自己跟自己交换 但是没有意义 所以直接让cur往后走
		else
		{
			cur++;
		}
	}
	//cur走到尾了  把keyi 放到 prev的位置
	Swap(&a[keyi], &a[prev]);
    //记录相遇的值
	int meet = prev;

	QuickSort3(a, begin, meet - 1);
	QuickSort3(a, meet+1,end);
}

 

快排优化方式二：小区间优化（本质是减少最后几层的递归操作，直接换为直接插入排序 堆排序 或者冒泡排序）  注：官方给出的是用直接插入排序，当然其他的也行。 而且小于多少层时用小区间优化那么取决你的数据大小是多少，最优的可以自己通过OP来进行测试

 

 

 

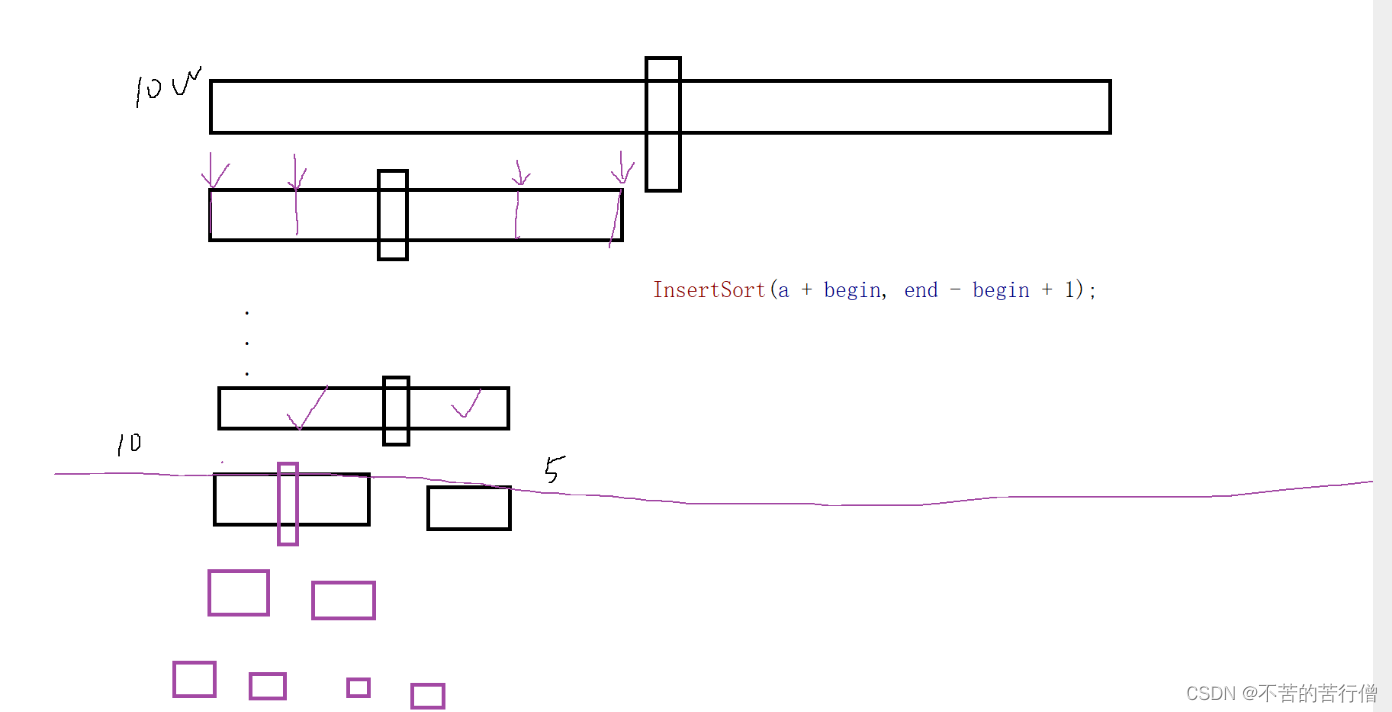
注意：当数据很少时 再用递归进行快排那么效率就没有那么高了，因为递归是非常消耗性能的。而且如果递归的层数太深，就会导致栈溢出 

 

//前后指针
void QuickSort3(int* a, int begin, int end)
{
	//对递归进行判断
	if (begin >= end)
	{
		return;
	}
		//三数取中
		int midIndex = GetMidIndex(a, begin, end);
		Swap(&a[begin], &a[midIndex]);

		int prev = begin, cur = begin + 1;
		//要记录下标  不能新建一个变量把a[begin]的值存起来 因为这样改变不了数组
		int keyi = begin;
	//数据多就用递归	
	if (end - begin > 20)
	{
		
		while (cur <= end)
		{
			//找小 （写法不唯一）
			if (a[cur] < a[keyi] && ++prev != cur) //先判断两个的值相不相等 再判断++prev 跟 cur等不等
			{
				Swap(&a[cur], &a[prev]);
			}
			//++prev == cur 说明自己跟自己交换 但是没有意义 所以直接让cur往后走
			else
			{
				cur++;
			}
		}
		//cur走到尾了  把keyi 放到 prev的位置
		Swap(&a[keyi], &a[prev]);
	}
	//不多就直接插入排序，这样可以减少递归 达到优化效果
	else
	{
		//HeapSort(a + begin, end - begin + 1);
		//a+begin：第begin个数据的地址
		InsertSort(a + begin, end - begin + 1);
	}
	
	//记录相遇的值
	int meet = prev;

	QuickSort3(a, begin, meet - 1);
	QuickSort3(a, meet + 1, end);
}

 

---

 

六.快速排序->挖坑法

 

其实大致思路跟hoare版本的差不了多少 都是两个指针 一左一右

思路：用一个变量ret把a[left]（左边第一个作为key的值）的值存起来， 然后同样的让key定在左边，那么我们就让 right先走，right找到比key小的数以后停下来 复制给 a[left]的位置 ，因为a[left]的数已经存下来的，这时候的a[left]的位置相当于一个坑 我们直接把数填进去就行。 right动完后到 left动 找大，同样的 因为a[right]的数据已经到了 a[left] 的位置 所以 a[right]的位置相当于一个坑  把left指向的数往坑上填就行  以此类推。

left right 相遇以后 说明都到了坑的位置 left主动撞的坑  然后直接把ret的值放进 a[left]位置就可以

然后记录相遇的位置， 继续递归 就可以了

 

 

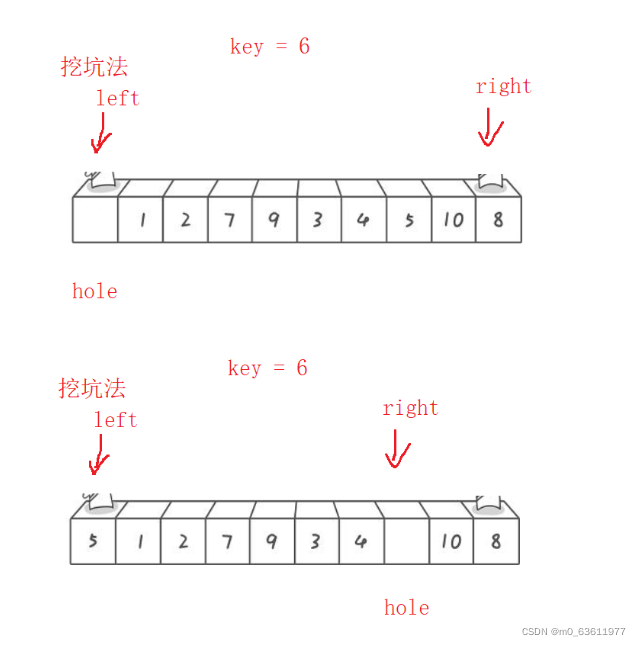
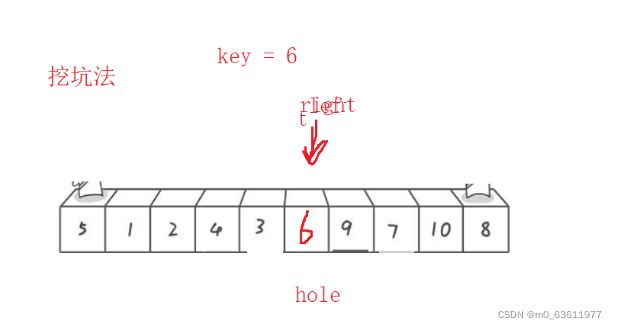
直接上代码

//挖坑法
void QuickSort2(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}

	int midIndex = GetMidIndex(a, begin, end);
	Swap(&a[begin], &a[midIndex]);

	int left = begin, right = end;
	//记录下最左边的位置 然后把该位置空出来 视为坑 对比后的数据就放到这个坑了
	//数据放进坑里后 那个数据原本的位置就也变成了坑 再把数据往里面放

    //用一个变量把key的数组记录下来
	int key = a[left];
	while (left<right)
	{
		//找小
		while (left < right && a[right] >= key)
		{
			//把right的数据给left以后  right的位置的数据就没有了 变成了个坑
			right--;
		}
		// 放到左边的坑位中,右边就形成新的坑
		a[left] = a[right];
		while (left < right && a[left] <= key)
		{
			left++;
		}
		// 放到右边的坑位中，左边就形成新的坑
		a[right] = a[left];
	}
	//相等说明已经对比完了  left跟right都在坑的位置  left主动遇坑
	a[left] = key;

	//此时 key有放在了该在的地方 记录相遇位置再次递归
	int meet = left;
	
	//[begin,meet-1] meet  [meet+1,end]

	QuickSort2(a, begin, meet - 1);
	QuickSort2(a, meet + 1, end);
}

---

 

七.快速排序 - > 前后指针法

 

定义两个记录下标的变量   思路再图上已经写有

 

 

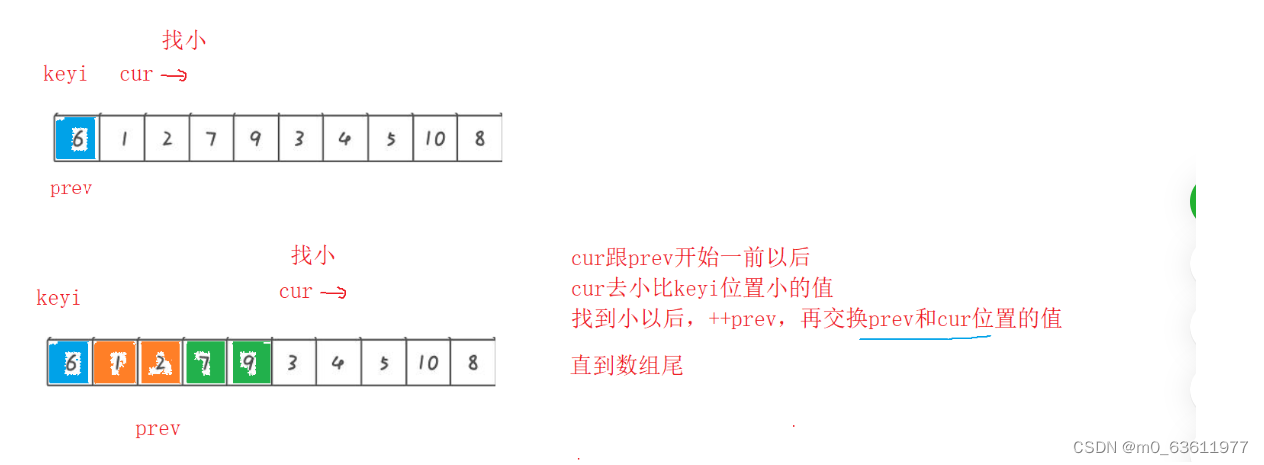
 直接上代码：

//前后指针
void QuickSort3(int* a, int begin, int end)
{
    //对递归进行判断
	if (begin >= end)
	{
		return;
	}
	// 为了避免最坏的情况  所以来个三数取中在进行快排
	int midIndex = GetMidIndex(a, begin, end);
	Swap(&a[begin], &a[midIndex]);

	int prev = begin, cur = begin + 1;
	//要记录下标  不能新建一个变量把a[begin]的值存起来 因为这样改变不了数组
	int keyi = begin;
	while (cur <= end)
	{
		//找小 （写法不唯一）
		if (a[cur] < a[keyi] && ++prev != cur) //先判断两个的值相不相等 再判断++prev 跟 cur等不等
		{
			Swap(&a[cur], &a[prev]);
		}
		//++prev == cur 说明自己跟自己交换 但是没有意义 所以直接让cur往后走
		else
		{
			cur++;
		}
	}
	//cur走到尾了  把keyi 放到 prev的位置
	Swap(&a[keyi], &a[prev]);
    //记录相遇的值
	int meet = prev;

	QuickSort3(a, begin, meet - 1);
	QuickSort3(a, meet+1,end);
}

 

---

 

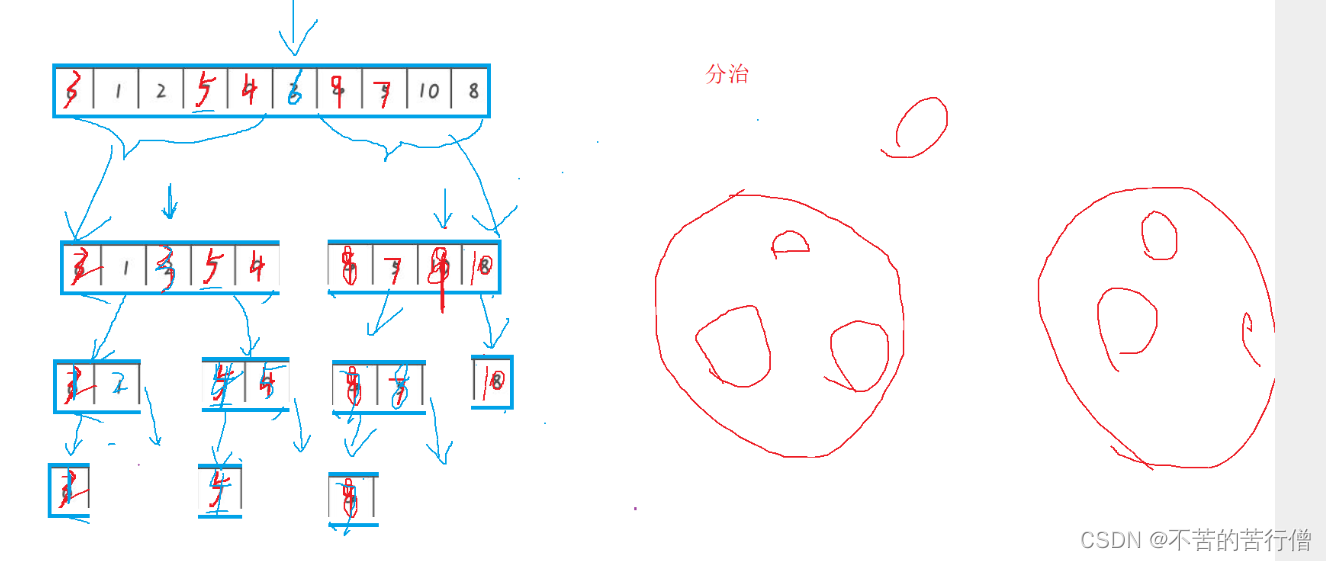
八.归并排序

思路：把一个数组用归并来分为左右两个部分（left - min）（min+1 right）分别再对这两个部分再进行递归，   开辟一个数组用来归并数据，归并完再把归并好的数据拷贝回原数组

 

 

 

 

 

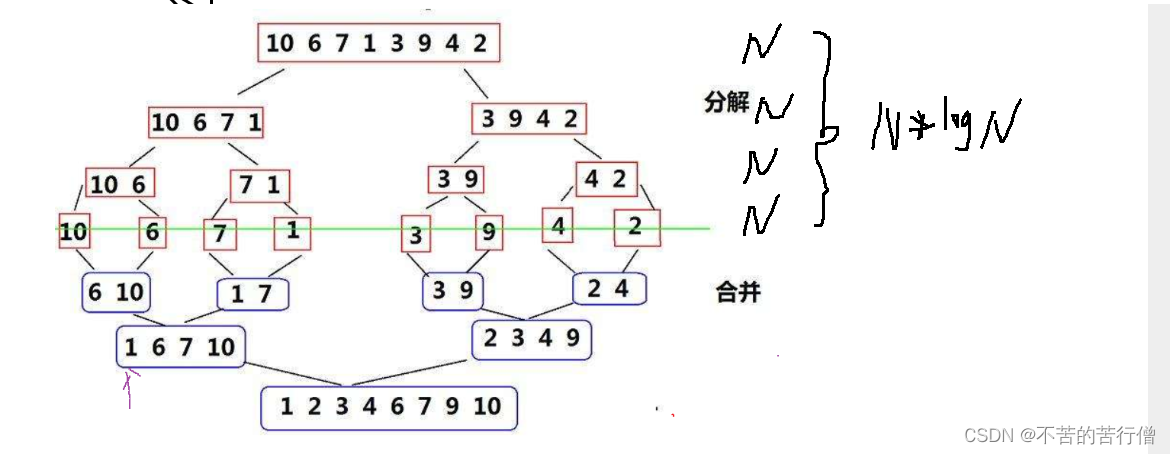
这里就直接上代码了，要是不了解的可以照着代码画图，感受一下归并的步骤。

//归并排序测试数据
void TestMergeSort()
{
	int a[] = { 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 };
	//int a[] = { 11, 9, 4, 3, 7, 1, 9, 8, 4, 3, 5, 0, 1, 3 };
	//int a[] = { 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, -1, -2, -3, -4, -5, -6, -7, -8, -9, -10, -11 };

	MergeSort(a, sizeof(a) / sizeof(int));
	PrintArray(a, sizeof(a) / sizeof(int));
}

//归并排序的核心算法
// 时间复杂度：O(N*logN)
// 空间复杂度：O(N)

void __MergeSort(int* a,int* tmp,int left,int right)
{
	if (left >= right)
	{
		return;
	}
    //算出中间值  除号效率低 所以用右移符号
	int min = (left + right) >> 1;

	//递归   [left,min-1] min [min+1,right]
    //也是类似于二叉树
	__MergeSort(a, tmp, left, min);
	__MergeSort(a, tmp, min+1, right);


    //因为两个部分不一定很均匀，也不一定从0开始 但是一定从left - right
    //比如递归到右边的时候的left 跟左边的left的下标值就不一样，这样拷贝回去的时候就会出现问题，所以我们要保持下标的一致性
	int i = left;

	int begin1 = left, end1 = min;
	int begin2 = min + 1, end2 = right;

    //两个部分，当一个部分走完 那么另一个部分就没有数跟他对比了，所以只要有一个走完
    //那么没有走完的那一部分就把剩下的数据存进 tmp 数组中就行
	while (begin1<=end1 && begin2<=end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}

	//把剩余的数直接拷贝到后面
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

	//归并完后把数据拷贝回到原来的数组a中
	for (int j = left; j <= right; j++)
	{
		a[j] = tmp[j];
	}
}

//归并排序
void MergeSort(int* a,int n)
{
	//开辟一个数组 用于数据的归并
	int* tmp = (int*)malloc(sizeof(int) * n);

    //因为开辟好空间后直接开始用归并排序来对数据进行排序就行
    //因此在这里进行了一个函数副用对归并算法单独出来，这样递归的时候就不用重复的开辟空间了
	__MergeSort(a, tmp, 0,n-1);


	//释放开辟的空间
	free(tmp);
}

 

---

 

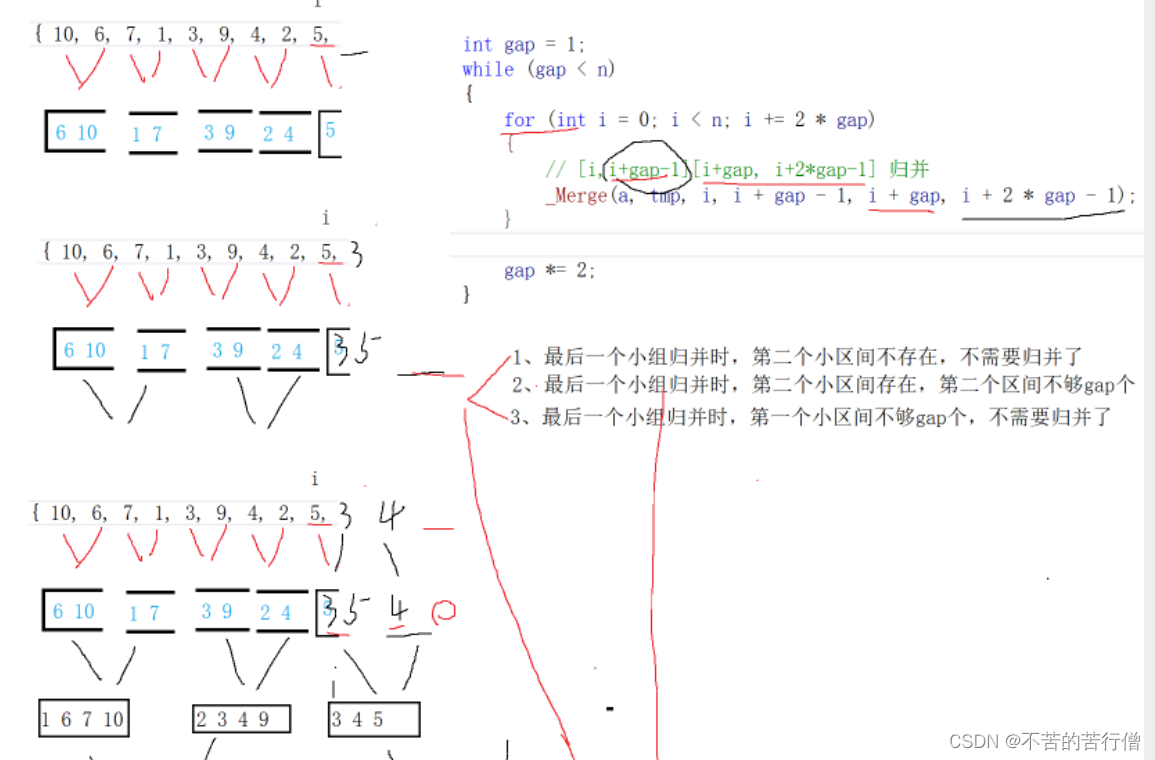
 九.并归排序（非递归方法）

我们知道 递归到最后一层以后 就是一个数跟一个数对比 左边 1 1  右边 1 1 然后返回到上一层  2 2比 在返回上一层 4  4 比

所以我们非递归的写法就是控制 gap

 

void _Merge(int* a, int* tmp, int begin1, int end1, int begin2, int end2)
{
	int j = begin1;
	int i = begin1;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
			tmp[i++] = a[begin1++];
		else
			tmp[i++] = a[begin2++];
	}

	while (begin1 <= end1)
		tmp[i++] = a[begin1++];

	while (begin2 <= end2)
		tmp[i++] = a[begin2++];

	// 归并完成以后，拷贝回到原数组
	for (; j <= end2; ++j)
		a[j] = tmp[j];
}

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int)*n);
	if (tmp == NULL)
	{
		printf("malloc failn");
		exit(-1);
	}

	int gap = 1;
    //不能改为 gap 《= 1/2n 因为这样走不到最后一个gap
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			// [i,i+gap-1][i+gap, i+2*gap-1] 归并
			int begin1 = i, end1 = i + gap - 1, begin2 = i + gap, end2 = i + 2 * gap - 1;

			// 如果第二个小区间不存在就不需要归并了，结束本次循环
			if (begin2 >= n)
				break;

			// 如果第二个小区间存在，但是第二个小区间不够gap个，结束位置越界了，需要修正一下
			if (end2 >= n)
				end2 = n - 1;

			_Merge(a, tmp, begin1, end1, begin2, end2);
		}

		gap *= 2;
	}

	free(tmp);
}

---

扩展（了解即可）

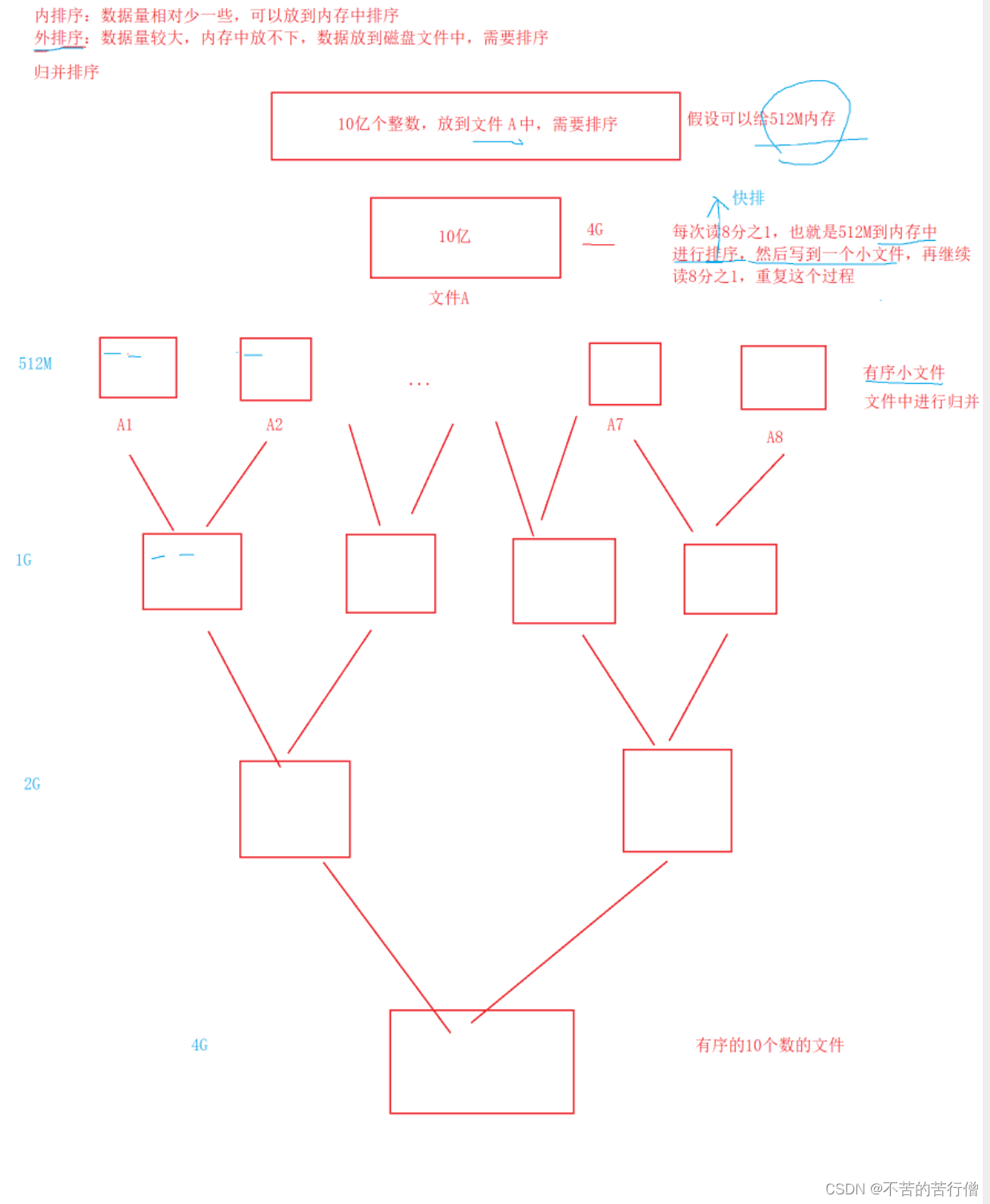
 归并排序即使内排序 也是外排序。

如果让你对10亿个数据进行归并排序 ，并且只给你512M的内存 那么你会怎么排序呢？

 

10亿个int类型数据就是 4G  我们分为八等分 每份1/8 先对这1/8在内存中进行排序再存进文件中（注意：这里不能用归并排序，因为归并排序要开辟一个等大小的空间 那么就会开辟一个10亿的 tmp 数组 那么就不符合要求了  所以除了归并排 我们可以选择任意一种） 排完1/8存进文件 再排序 1/8 再存 直到把八分存完 然后再两两归并排 

 

 

---

十. 非比较排序（前面学的都是比较排序）

 

该算法对比较集中的数据才会有很大效果

非比较排序就算对一个数组的数据进行排序，但是不是通过对比的方式选出小的存在左边。而是统计每个数据出现的次数，然后存进另一个数组对应的下标的位置 

非比较排序分为两种： 绝对映射  相对映射

 

// 时间复杂度：O(N+range)
// 只适合，一组数据，数据的范围比较集中. 如果范围集中，效率是很高的，但是局限性也在这里
// 并且只适合整数，如果是浮点数、字符串等等就不行了
// 空间辅助度：O(range)
void CountSort(int* a, int n)
{
    //找出最大最小值 好确定数据集中的区间
	int max = a[0], min = a[0];
    //选出最大值 最小值 虽然给出的数组大小是n 但是我们的算法所开辟的空间并不一定需要n
    //比如0 0 1 1 1 2 2 2 3 3 3   这里有11个数 但是我们要统计每次数字出现的次数然后存进相对下标就行    a[0] = 2次  a[1] = 3     a[2] = 3  a[3] = 3  所以我们只需要开辟大小为3的新数组就行
	for (int i = 0; i < n; ++i)
	{
		if (a[i] > max)
			max = a[i];

		if (a[i] < min)
			min = a[i];
	}
    
    //最大值 - 最小值就是中间有的最多的个数 用来开辟数组
	int range = max - min + 1;
	int* count = malloc(sizeof(int)*range);
    //初始化为0  不然就会是一个随机值 那么就不能够统计出来想用数字出现的个数了
	memset(count, 0, sizeof(int)*range);
    //统计每个数出现的次数
	for (int i = 0; i < n; ++i)
	{
        //a[i]的值 - min（最小值） 就是相对位置 比如 15 - 10 = 5  那么就把15存在下标为a【5】的位置 统计出现的次数
		count[a[i] - min]++;
	}

    
	int i = 0;
	for (int j = 0; j < range; ++j)
	{
        //拷贝回原来的数组 次数为0的就不打印
		while (count[j]--)
		{
			a[i++] = j + min;
		}
	}

     //释放空间
	free(count);
}

---

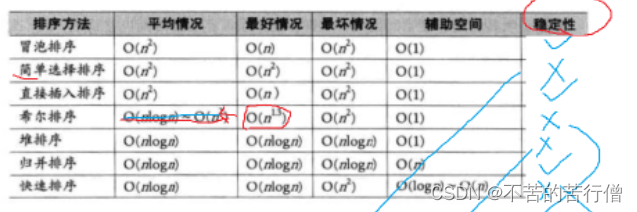
扩展（面试经常会问复杂度 稳定性） 

 

 书上很多选择排序都写的是稳定，但是没有考虑到当 选大时 大的那个数换到了最后面，而最后面的数据正好是连续的 那么就打乱了顺序了   比如 1 2 3 9 5 5 5  这时候就变成了 1 2 3 5 5 5 9 这时候的这三个五的位置已经发生了变化了，所以是不稳定的

 

 

 

 

 

 

 

最后

以上就是纯真香烟为你收集整理的（C语言）七大常见排序算法之 详解版 -＞（希尔 快排 冒泡 归并排等）的全部内容，希望文章能够帮你解决（C语言）七大常见排序算法之 详解版 -＞（希尔 快排 冒泡 归并排等）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。