堆排序以及堆排序优化

class HeapSort:
    # 堆排序：先将数组中的数据通过heapInsert生成大根堆
    # 生成大根堆之后，将头与最后一个交换，此时最后一个为最大值，heapSize-1
    # 将交换后的堆通过heapify再生成大根堆，再交换，重复如此步骤，此为堆排序
    # 堆排序额外空间复杂度O(1)
    def heapsort(self, arr):
        if arr is None and len(arr) < 2:
            return
        # O(N*logN)
        for i in range(len(arr)):
            self.heapInsert(arr, i)

        heapSize = len(arr)
        heapSize -= 1
        self.swap(arr, 0, heapSize)
        while heapSize > 0:
            self.heapify(arr, 0, heapSize)
            heapSize -= 1
            self.swap(arr, 0, heapSize)

    def heapInsert(self, arr, index):
        while arr[index] > arr[(index-1) /2]:
            self.swap(arr, index, (index-1)/2)
            index = (index-1)/2

    def heapify(self, arr, index, heap_size):
        left = index * 2 + 1
        while left < heap_size:
            # 左右两个孩子中，谁大，谁把自己的下标给largest
            # 右 -> 1)有右孩子 && 2）右孩子的值比左孩子大才行
            # 否则，左
            largest = left + 1 < heap_size and left + 1 if arr[left + 1]>arr[left] else left
            largest = largest if arr[largest] > arr[index] else index
            if largest == index:
                break
            self.swap(arr, largest, index)
            index = largest
            left = index * 2 + 1

    def swap(self, arr, i, j):
        temp = arr[i]
        arr[i] = arr[j]
        arr[j] = temp

大根堆的优化：
时间复杂度从#O(N*logN)到O(N) 。从下往上看

for i in range(len(arr)-1, -1, -1):
	self.heapify(arr, i, len(arr))

证明优化的大根堆时间复杂度为O(N)

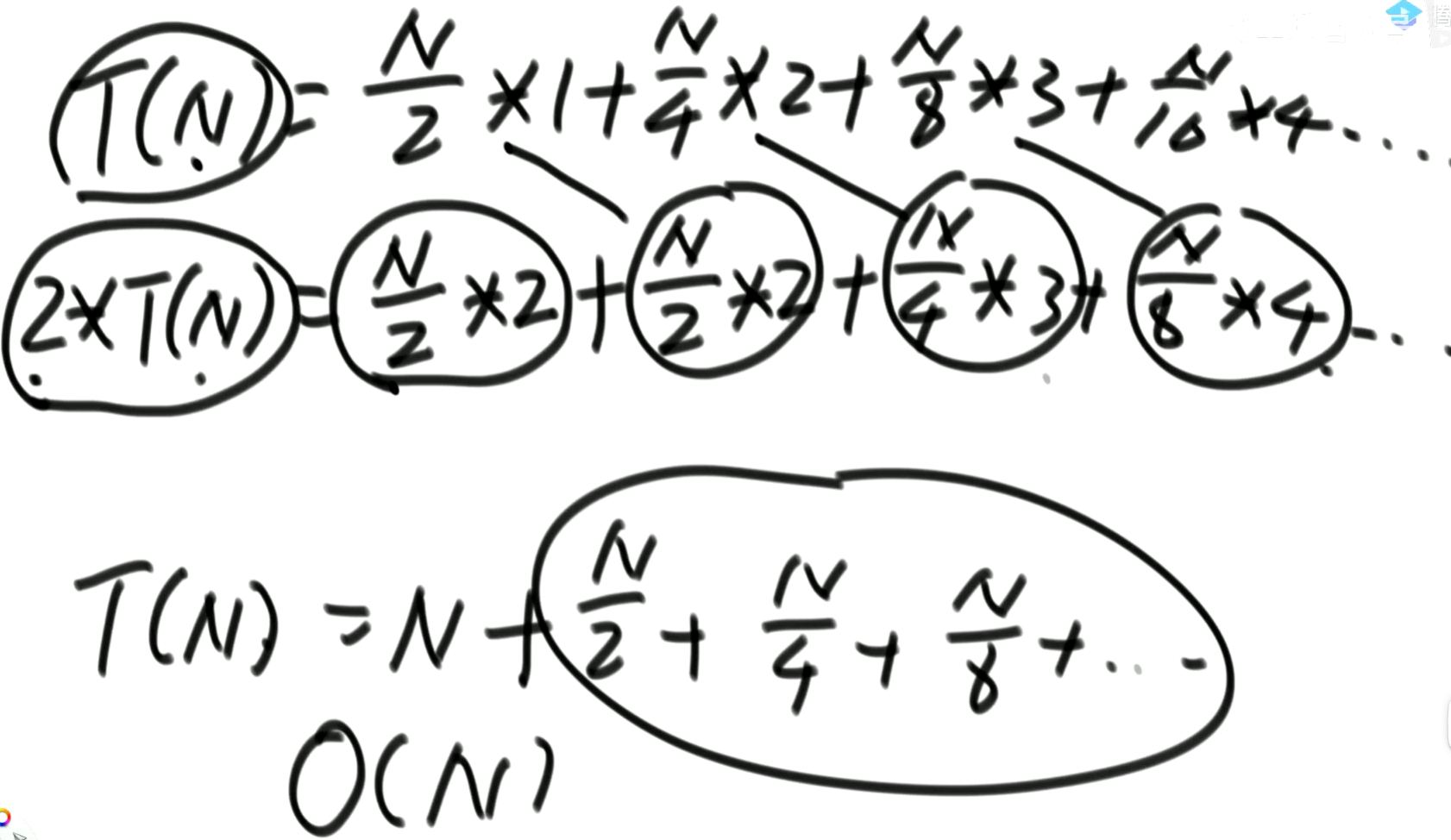
解题思路：
假如k=5，先将0-5生成小根堆，将最小的拿出来放到数组的第一个，然后是1-6生成小根堆，将最小的拿出来放到数组的第二个，然后是2-7 …以此类推

最后

以上就是傲娇眼神为你收集整理的堆排序以及堆排序优化的全部内容，希望文章能够帮你解决堆排序以及堆排序优化所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。