C 环境
# 使用下面的命令来检查您的系统上是否安装了 GCC
gcc -v
# 如果没有安装 使用下面命令安装
apt install gcc
时间复杂度
| 算法 | 时间复杂度 | 稳定性 |
|---|---|---|
| 冒泡 | O(n^2) | 稳定 |
| 选择 | O(n^2) | 不稳定 |
| 插入 | O(n^2) | 稳定 |
| 希尔 | 平均 O(nlogn) 最差O(n^2) | 不稳定 |
| 快速 | 平均 O(nlogn) 最差O(n^2) | 不稳定 |
| 归并 | O(nlogn) | 稳定 |
| 堆 | O(nlogn) | 不稳定 |
| 基数 | O(kn) | 稳定 |
排序算法
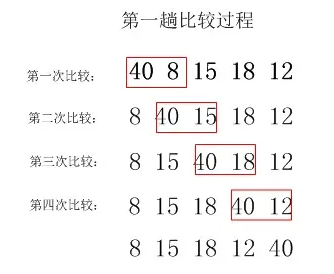
冒泡排序
比对 的双方 放在一个盒子中, 盒子 就像泡泡一样,一步一步冒出去。
#include <stdio.h>
// 程序运行命令 gcc main.c -o aaa; ./aaa
int main()
{
int arr[] = {4, 2, 1, 3,5, 10, 11,2,3,1};
int len = sizeof(arr)/sizeof(arr[0]);
bubbleSort(arr, len);
printf("[ ");
int i;
for (i = 0; i < len; i++)
printf("%d, ", arr[i]);
printf("]");
printf("n");
return 0;
}
void bubbleSort(int *arr, unsigned int length)
{
if (length < 2)
return; //长度小于2的数组 无需排序
int i; // 轮数 计数器
int j; // 每轮 比对数 计数器
int tmp; // 变量交换的临时变量
for (i = 0; i < length - 1; i++) //总的执行多少轮
{
// 从前往后,两两比,每轮最大值放后面
for (j = 0; j < length - 1 - i; j++) //每轮执行的次数
{
if (arr[j] > arr[j + 1])
{
tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
}
选择排序
熊瞎子剥玉米,一轮过去手里只有一个最大(小)的。

void selectionSort(int *arr, unsigned int length)
{
if (length < 2)
return; //长度小于2的数组 无需排序
int i;
int j;
int tmp;
for (i = 0; i < length - 1; i++)
{
int min = i;
// 从前往后,每一轮的 首个元素 依次和后面元素对比, 将 最小的 放在每一轮的首位置
for (j = i + 1; j < length; j++)
{
if (arr[min] > arr[j])
{
min = j;
}
}
tmp = arr[min];
arr[min] = arr[i];
arr[i] = tmp;
}
}
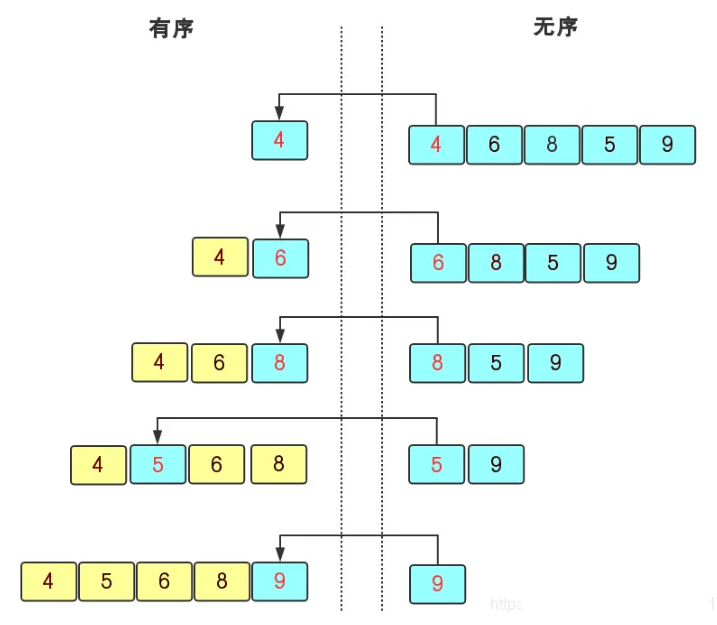
插入排序
抓扑克排序
void insertSort(int *arr, unsigned int length)
{
if (length < 2)
return; //长度小于2的数组 无需排序
int i;
int j;
int current; // 当前比对元素
for (i = 1; i < length; i++)
{
current = arr[i];
// 从已排序的最右边开始,把大于 当前排序 的元素 后移
for (j = i - 1; j >= 0; j--)
{
// 如果找到 当前排序元素 比 有序序列中 大的元素,就证明 前面的元素都会 比 前排序元素, 则此轮无需再找,直接跳出循环
if (current >= arr[j])
break;
// 有序序列中 大于 当前比对元素 的元素 后移一位
arr[j + 1] = arr[j];
}
// 将 当前比对元素 放到 比较过程中,最后一次比较的元素 后面
arr[j + 1] = current;
}
}
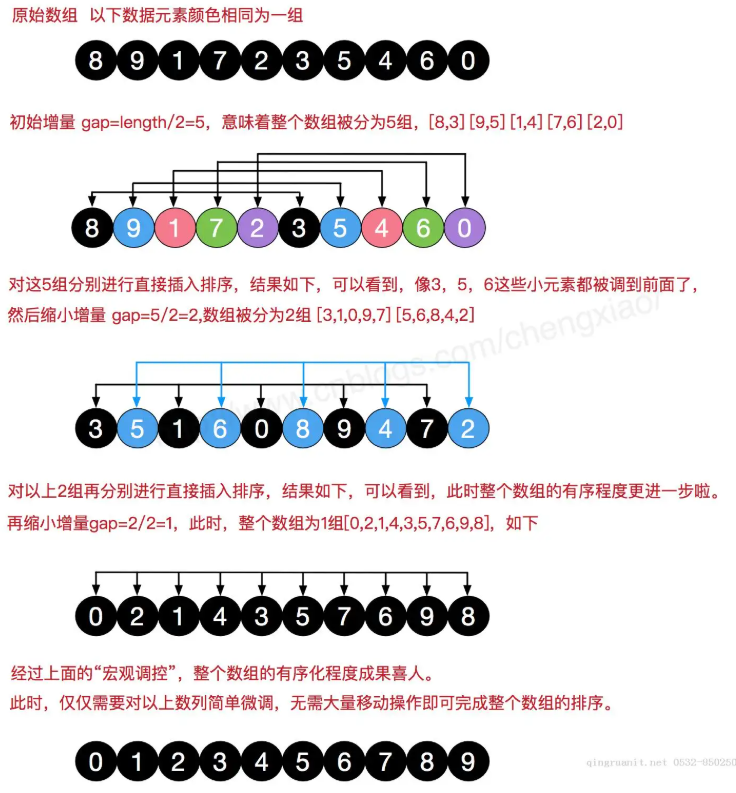
希尔排序
插入排序的升级版本, 分组之后 在进行插入排序
void shellSort(int *arr, int length)
{
int i, step; // 步长
// 强类型语言中: 3/2 == 2/2 == 1,
// 所以 每次取一半, 最后一次步长 必定为1
for (step = length / 2; step > 0; step = step / 2)
{
printf("此次分组的步长:%dn", step);
// 步长 为几, 就将原数组 分成 几组,
// 对 ===每一组=== 都进行 插入排序
for (i = 0; i < step; i++)
{
InsertSortByStep(arr, length, i, step);
}
}
}
// length 数组总长度; i 分组的起始位置; step 步长(增量)
void InsertSortByStep(int arr[], int length, int i, int step)
{
int current; // 当前排序元素
int current_index; // 当前排序元素 的 计时器
int j; // 插入时,需要后移元素 的计数器
for (current_index = i + step; current_index < length; current_index=current_index+step)
{
current = arr[current_index];
for (j = current_index - step; j >= 0; j = j - step)
{
if (current >= arr[j]) break;
// 有序序列中 大于 当前比对元素 的元素 后移一位
arr[j + step] = arr[j];
}
// 将 当前比对元素 放到 比较过程中,最后一次比较的元素 后面
arr[j + step] = current;
}
}
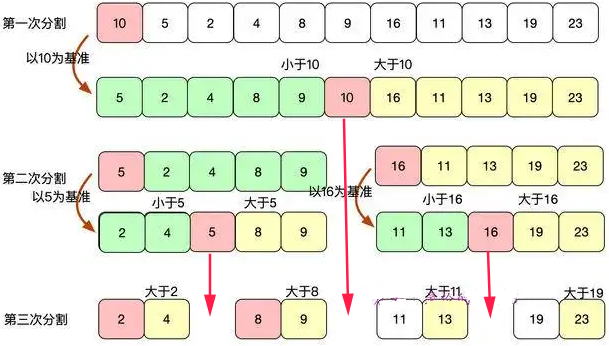
快速排序
/*
1 从数列中取出一个数 作为 基准数
2 扫描数列, 将小于基准数的放在左侧, 大于的放在右侧,得到两个区间。
3 在对 两个区间 进行递归
*/
void quickSort(int *arr, int length)
{
if (length<2) return; //递归的结束条件
int center = arr[0]; // 选最左侧的 数 作为中心轴
int left = 0; // 左下标
int right = length-1; // 右下标
int moving = 2; // 当前应该移动 哪边的坐标, 1:左下标 2:右下标
// 交替式 移动, 左下标 比较大小时 如果 移动了元素到 右侧, 则下次循环 就 比较 左下标,反复交替,
// 直到 左下标==右下标, 当 两标 重合,证明此轮排序完成
while (left < right)
{
if (moving ==2) // 移动右下标的case
{
// 如果右下标位置元素的值 大于等于 中心轴, 继续移动 右下标
if (arr[right] >= center)
{
right--; // 此次比对 没有找到 比中心轴小的,则无需移动比对元素,比对 右侧的 下一个元素
continue;
}
// 如果右下标位置元素的值 小于 中心轴, 把它填到左下标的坑中
arr[left] = arr[right];
left++; //左下标向由移动
moving = 1; // 右边移动了元素,空出坑了,那么下次循环将移动 左下标
continue;
}
if (moving ==1) // 移动左下标的case
{
// 如果左下标位置元素小于等于 中心轴,继续移动左下标
if (arr[left]<=center)
{
left++;
continue;
}
// 如果左下标位置元素的值大于中心轴, 把它填到右下标的坑中
arr[right] = arr[left];
right--;
moving= 2; // 左边移动了元素,空出坑了,那么下次循环将移动 右下标
continue;
}
}
// 如果循环结束,把 中心轴 的值 放回去
arr[left] = center;
quickSort(arr, left); // 对中心轴 左边 的序列进行排序
quickSort(arr + left+1, length-left-1); // 对中心轴 右边 的序列进行排序
}
合并排序
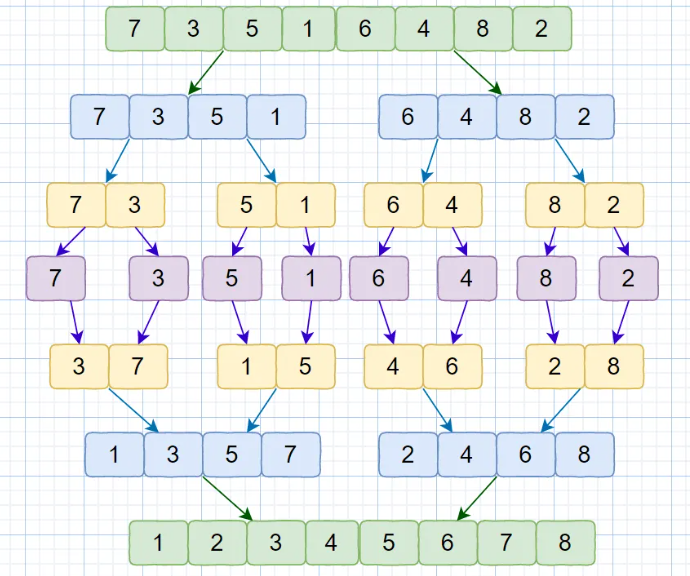
// A 待排序数组
// begin 索引起始位置 0
// end 索引终止位置 len-1
void MERGE_SORT(int *A, int begin, int end)
{
if (begin < end) //递归结束条件, 数组只有一个元素时 结束
{
int mid = (begin + end) / 2; // 计算中间元素下标,将数组 分为 左右两个部分
MERGE_SORT(A, begin, mid); // 左部分 递归
MERGE_SORT(A, mid + 1, end); // 右部分 递归
MERGE(A, begin, mid, end); // 合并 左半部分 和 右半部分
}
}
// b 第一个元素索引; m 中间元素索引; e 最后一个元素索引
void MERGE(int *A, int b, int m, int e)
{
int l = m - b + 1; // 左半部分 数组长度
int L[l]; // 存放 左半部分 的外部数组
int r = e - m; // 右半部分 数组长度
int R[r]; // 存放 右半部分 的外部数组
int i, j, k;
// 下面两个循环,分别将 已排序的 左、右半部分 的 原始数组元素 拷贝到 左、右外部数组
for (i = 0; i < l; i++)
{
L[i] = A[b + i];
}
for (j = 0; j < r; j++)
{
R[j] = A[m + j + 1];
}
i = 0; // 左 外部数组 的索引
j = 0; // 右 外部数组 的索引
k = b; // 原始数组 的 索引
// 合并函数 的 核心, 分为3种情况:
// case1: 左、右 外部数组 都有元素待 比较合并 的情况
while (i < l && j < r)
{
// 通过 k 指定 原始数组 首个要 放入 外部数组 的一个坑位
// 哪个外部数组的 元素小 就 放到 原始数组 的坑中
if (L[i] <= R[j])
{
A[k] = L[i];
i++;
}
else
{
A[k] = R[j];
j++;
}
k++; // 指定 原始数组 的下一个坑位
}
// case2: 右 外部数组 元素都比较合并完了,只剩下 左 外部数组 的情况
while (i < l)
{
A[k] = L[i]; // 将 左 外部数组 元素 依次放入到 原始数组 中
i++;
k++;
}
// case3: 左 外部数组 元素都比较合并完了,只剩下 右 外部数组 的情况
while (j < r)
{
A[k] = R[j]; // 将 右 外部数组 元素 依次放入到 原始数组 中
j++;
k++;
}
}
堆排序
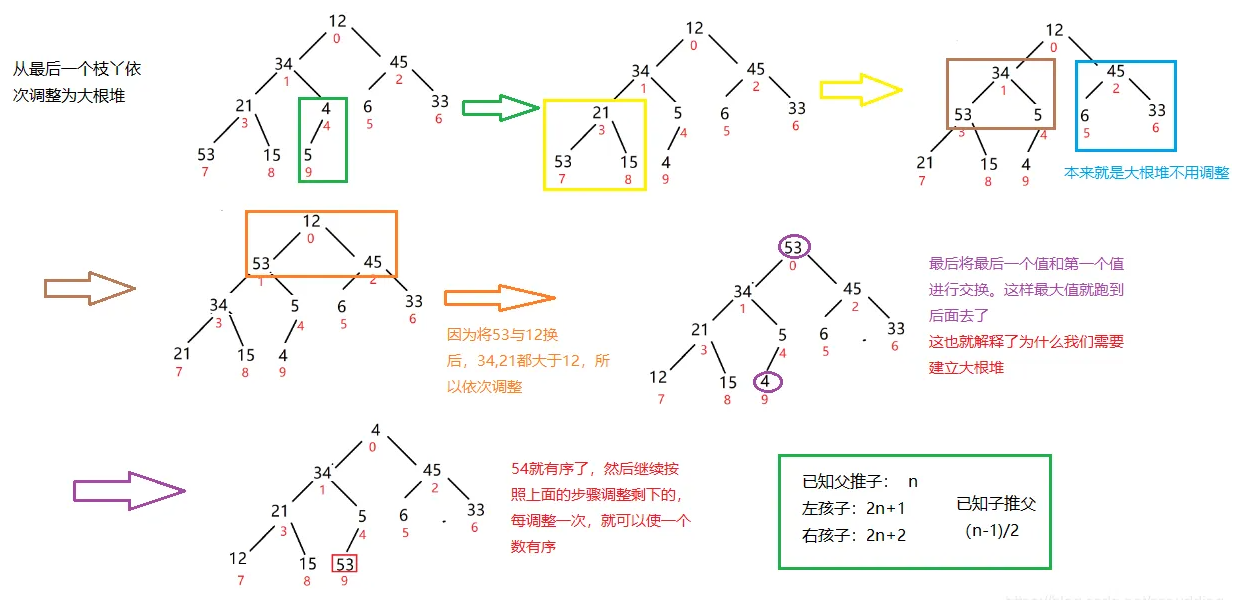
/*
首先明确, 数组 存储二叉树 时 数组索引 和 父子节点的关系:
父节点的索引为 n, 则左子节点为: 2n, 右子节点为 2n+1;
因为 强类型语言中, 2/2 == 3/2 == 1,
所以 左、右子节点 的 索引为 x, 则 父节点 都为 x/2;
*/
//堆排序
void HeapSort(int arr[],int len)
{
// step1: 创建大顶堆,
int last=len-1; //最后一个 叶子结点 (即 数组的最后一个索引)
int parent=last/2; //最后一个 叶子结点 的 父结点
for(int i=parent;i>=0;i--)
{
Heapify(arr,len,i); //从最后一个父结点开始做大顶堆调整
}
// step2: 反复 交换 顶根节点,然后再 调整大顶堆
for(int i=len-1;i>=0;i--)
{
// 将 顶根节点 与 最后一个节点(按照层次遍历) 交换位置
swap(arr,i,0);
// 调整 交换位置 后的 二叉树 为 大顶堆
Heapify(arr,i,0);
}
}
//节点位置交换
void swap(int arr[],int i,int j)
{
int temp;
temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
//大顶堆调整
void Heapify(int arr[],int len,int k)
{
if(k<len)
{
int max=k;//根结点
int s1=2*k;//左子节点
int s2=2*k+1;//右子结点
// 比较 左、右子节点, 谁大 就把谁的索引 赋值为 节点索引
if(arr[s1]>arr[max]&&s1<len)
max=s1;
if(arr[s2]>arr[max]&&s2<len)
max=s2;
// 递归结束条件: 根节点 大于 左右子节点 的情况 or 当假设的根节点max 没有子节点时(其实是 叶子节点时)
if(max!=k)
{
swap(arr,max,k); // 将 根节点 和 子节点 交换位置
Heapify(arr,len,max); // 再进行堆调整
}
}
}
基数排序
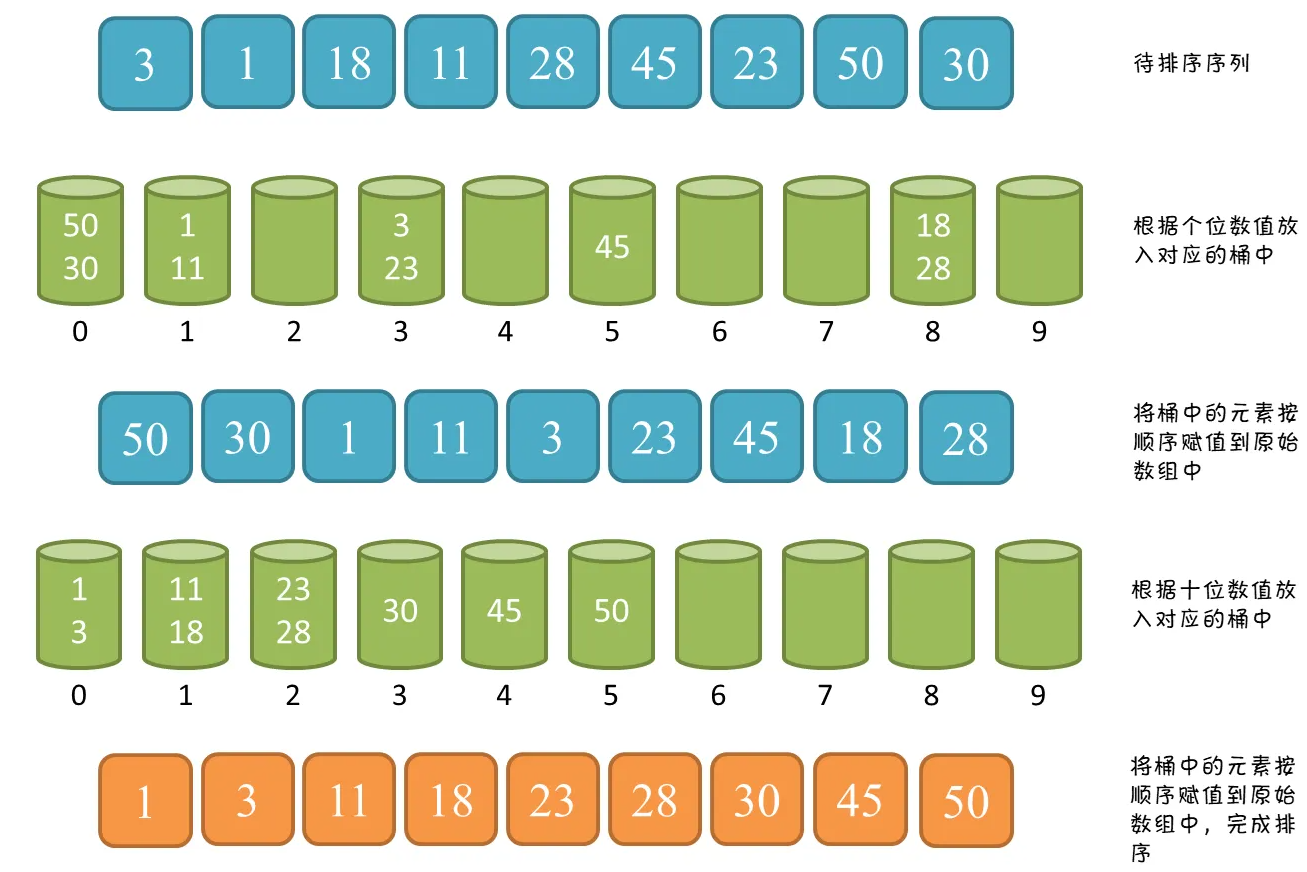
void RadixSort(int *arr, int length)
{
// step1: 分配、收集 的轮数 由 最大的数决定, 所以先 确定最大值
int i,
max = arr[0]; // 最大值
for (i = 1; i < length; i++)
{
if (arr[i] > max)
max = arr[i];
}
// step2: 分配、收集
int base = 1; // 排序指数,从个位数开始(base=1 按个位排序; base=10 按十位排序 ......)
int tmp[length]; // 收集空间:定义一个 和 排序数组 等大的 临时数组,用于存放 收集时的元素
// 分配、收集 的轮数 由 最大的数决定, 如 最大数123: 第一轮 123/1 满足条件; 第二轮 123/10 满足条件; 第仨轮 123/100 满足条件; 第四轮 123/1000 不满足条件;
while (max / base > 0)
{
// 定义 10 个桶 (索引 0---9)
int bucket[10] = {0};
// 2-1: 统计出 各个桶中 存放的 元素个数
for (i = 0; i < length; i++)
{
// 计算出 应该放入哪个桶,
int bucket_which = arr[i] / base % 10; // 例:123 取个位上的数: 123 /1 %10 = 3, 取十位上的数: 123/10 % 10=2
// 对应的桶 树枝上加一,
bucket[bucket_which]++; // 桶位的元素数值 代表 该桶 里放置的元素个数
}
// 2-2: 计算 每个桶 前面的 所有桶 已经放置 元素的个数
for (i = 1; i < length; i++)
{
// 此时每个桶的 数值 不再表示 桶盛放 元素的个数, 而是 统计 前面的桶 到 当前的桶 一共放置的 元素个数
bucket[i] += bucket[i - 1]; // 例:索引0的桶有2个元素,索引1桶0个,索引2桶1个元素, 则:bucket[0]=2; bucket[1]=2; bucket[2]=3;
}
// 2-3: 收集元素 到 收集空间, 重点 确定 收集元素 时的 元素索引,
/* 举例:
索引为0的桶 有 2个元素, 索引1的桶 0个元素, 索引2桶 1个元素, 索引3桶有2个元素,则
索引3桶中,先入的那个元素的 数组索引为: (2+0+1+2)-1;
同理 索引2桶 元素的 数组索引为: (2+0+1)-1
*/
for (i = length - 1; i >= 0; i--)
{
/* 举例: 4、2、1、3、5
桶: 0、1、2、3、4、5、6、7、8、9
放置个数:0、1、1、1、1、1、0、0、0、0
放置总数:0、1、2、3、4、5、0、0、0、0
从后往前收集: 对于元素 5
对应桶: 5号桶
收集索引:5号桶 元素值 -1 = 4
此时放置总数:0、1、2、3、4、4、0、0、0、0
*/
// 首先计算出 收集的元素 在 哪个桶 中,
int bucket_where = arr[i] / base % 10;
// 再确定 该桶 之前 总共放置的 元素个数(即 前一个桶的 记录的数值),得到 该元素 在 收集空间的 索引
int tmp_index = bucket[bucket_where] - 1;
// 将 元素 放入 到 指定位置的 收集空间 中
tmp[tmp_index] = arr[i];
// 收集完一个 元素, 对应 桶 中的数值也要 减一
bucket[bucket_where] -= 1; // 例如 bucket[2] 中被收集掉一个元素, 对应 bucket[3]而言, 前面总的 收集元素个数 就少了一个, 所以要进行-- 操作
}
// 2-4: 将 收集空间 的元素, 保持位置地 挪移到 原数组中,这个就完成了一轮 分配、收集。
for (i = 0; i < length; i++)
{
arr[i] = tmp[i];
}
base *= 10; // 进入下一轮之前 要 将 排序指数 增加 一个数量级,即 扩大十倍(十进制)
}
}
最后
以上就是凶狠信封最近收集整理的关于经典排序算法(C语言)C 环境时间复杂度排序算法的全部内容,更多相关经典排序算法(C语言)C内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复