前言

tmd，哪个天杀的狗东西想出来的这么一个装饰品！！！
我刷了半小时！！！
就一只！！！
还让我给弄成这么个破玩意！！！

太上头了，得来一道线段树消消气。

A Greeting from Qinhuangdao(组合数学)

比赛链接：https://codeforces.com/gym/102769/problem/A

题目大意

现在你有r个红气球和b个蓝气球。
现在我们从其中一次性拿出两个气球，这两个气球都是红气球的概率是多少？

结果请以分数形式给出。
若概率为0请输出0/1，若概率为1则输出1/1，否则请输出最简分子式。

思路

简单的组合数学：

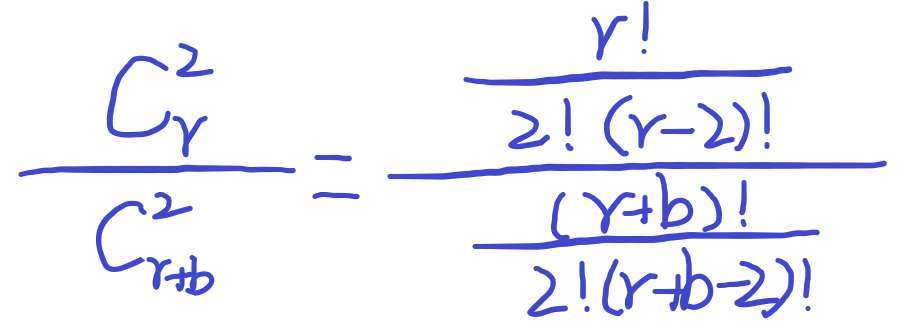
AC代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;

int main()
{
    int t;
    cin>>t;
    int cnt=0;
    while(t--)
    {
        ll r,b;
        cin>>r>>b;
        ll ans=r*b+r*(r-1)/2+b*(b-1)/2;  //化简分母
        ll ans2=r*(r-1)/2;               //化简分子
        if(ans2==0) cout<<"Case #"<<++cnt<<": 0/1"<<endl;
        else if(ans2==ans) cout<<"Case #"<<++cnt<<": 1/1"<<endl;
        else{
            ll x=__gcd(ans,ans2);       //最简分子式，去除上下最大公约数
            cout<<"Case #"<<++cnt<<": "<<ans2/x<<"/"<<ans/x<<endl;
        }
    }
}

Exam Results(枚举+贪心)

比赛链接：https://codeforces.com/gym/102769/problem/E

题目大意

$Alex$教授正在准备一场考试，一共会有$N$名学生参加。
如果在考试当天，学生$i$的状态拉满，他的分数就可以稳定在$a_i$；否则他的分数就稳定在$b_i$。
我们假设所有同学的考试成绩中最高分为point，则分数超过point*p%的同学可以通过本次考试。
每个人在考试时的状态我们是无法预测的。

$Alex$想知道最多会有多少名学生可以通过考试。

思路

老话说得好：年夜饭吃什么取决于孩子的期末成绩，考的好吃饺子，考不好吃孩子。
博主能安全活到现在，也是总结出了自己的一点点心得：不会真有人会挂科吧？不会真有人不及格吧？
(博主的高中物理从来没有及格过)

闲话少说，我们来看这道题。
通过题目我们能看出：通过考试的学生数量和这个最高分point密切相关，所以LJ博主的办法就是枚举最高分point的值。然而这道题的数据量并不小，我们不能写得过于暴力，要动点脑子。

最高分point的最大值是很好找的，$max${$a_i$}呗。那最高分point的最小值呢？
——$max${$b_i$}。
那么最高分point的取值范围就是$[max${$b_i$}，$max${$a_i$}$]$，慢慢枚举就好了。

枚举过程中还会有个问题：判断某个学生的分数score是否可以通过考试，即score与point*p%的比较。
这个简单，两边同乘$100$即可。但这样可能会爆精度，需要开$longlong$。

AC代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=2e5+100;
struct node
{
    ll a,b;
} score[maxn];

bool cmp(node x,node y)
{
    return x.a>y.a;
}
int main()
{
    ios::sync_with_stdio(false);
    int t;
    cin>>t;
    int cnt=0;
    while(t--)
    {
        int n,p;
        ll maxb=-1;
        cin>>n>>p;
        for(int i=1; i<=n; i++)
        {
            cin>>score[i].a>>score[i].b;
            maxb=max(score[i].b,maxb);
        }
        sort(score+1,score+1+n,cmp);
        ll ans=-1;
        for(int i=1; i<=n&&score[i].a>=maxb; i++)
        {
            ll tmp=1;
            //思考：为什么写两个for循环？为什么不写成一个？
            for(int j=1; j<i; j++)
            {
                if(score[j].b*100>=score[i].a*p){
                    tmp++;
                }
            }
            for(int j=i+1; j<=n; j++)
            {
                if(score[j].a*100>=score[i].a*p){
                    tmp++;
                }
                else
                    break;
            }
            ans=max(tmp,ans);
        }
        //不要忘记point取最小值的情况
        //因为这个WA两发可不值得
        ll tmp=0;
        for(int i=1;i<=n;i++)
        {
            ll s=score[i].b;
            if(score[i].a<=maxb)
                s=score[i].a;
            if(s*100>=maxb*p)
                tmp++;
        }
        ans=max(tmp,ans);
        cout<<"Case #"<<++cnt<<": "<<ans<<'n';
    }
}

Friendly Group(并查集)

比赛链接：https://codeforces.com/gym/102769/problem/F

题目大意

$Alex$教授打算安排一部分学生去参加一个学术会议。
$Alex$教授有$n$个优秀的学生，他打算从其中选出$k(k>=0)$个学生组成一个学习小组参加会议。
学习小组有友好度这一属性，小组友好度=小组间朋友对数 - 小组人数。
这n个学生之间有m对朋友关系。

现在问你，学习小组的友好度最大可以是多少？

思路

感觉上是入门级别的并查集，但需要加一点东西。

定义一维数组edge与一维数组point，意义如下：

edge[i]:以第i个同学为核心的小团体有多少个朋友关系。
point[i]:第i个同学所在的小团体的人数，一开始所有人属于只有自己的小团体，edge[i]=1。

如果学生A与学生B之间具有朋友关系，会出现两种情况：

1. 学生A与学生B属于同一团体→这个团体的朋友关系数量+1；
2. 学生A与学生B不属于同一团体→让学生A的团体归于学生B的团体，重新形成以学生B为核心的团体。
   此时以学生B为核心的团体的人数需要加上学生A的团体的人数；
   以学生B为核心的团体的朋友关系数量需要加上学生A的团体的朋友关系数量，再额外+1(A，B之间的关系)；

最后注意不要重复计算同一个团体的贡献值。

AC代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=3e5+100;

int pre[maxn];
int rankk[maxn];
bool vis[maxn];
int edge[maxn];
int point[maxn];

void init(int n)
{
    for(int i=1;i<=n;i++)
    {
        pre[i]=i;
        rankk[i]=1;
        edge[i]=0;
        point[i]=1;
        vis[i]=false;
    }
}

int findfa(int x)
{
    if(pre[x]==x)
        return x;
    else
        return pre[x]=findfa(pre[x]);
}

void join(int x,int y)
{
    x=findfa(x);
    y=findfa(y);
    if(x==y){
        edge[y]++;
        return;
    }
    if(rankk[x]>rankk[y])
        pre[y]=x;
    else
    {
        if(rankk[x]==rankk[y])
            rankk[y]++;
        pre[x]=y;
    }
    edge[y]+=edge[x]+1;
    point[y]+=point[x];
}

int main()
{
    ios::sync_with_stdio(false);
    int t;
    cin>>t;
    int cnt=0;
    while(t--)
    {
        int n,m;
        cin>>n>>m;
        init(n);
        for(int i=1;i<=m;i++)
        {
            int x,y;
            cin>>x>>y;
            join(x,y);
        }
        int ans=0;
        for(int i=1;i<=n;i++)
        {
            if(!vis[pre[i]])
            {
                vis[pre[i]]=true;
                ans+=(edge[pre[i]]-point[pre[i]]>0)?(edge[pre[i]]-point[pre[i]]):0;
            }
        }
        cout<<"Case #"<<++cnt<<": "<<ans<<endl;
    }
}

后话

感谢阅读，希望能对你产生一点用处。

以下台词取自《银魂》第211集——四天王篇：
(婆婆与银时的首次相遇时的对话，首次出现于《银魂》第12集凯瑟琳登场)
(每个雨夜都会让我想起这一片段)

最后

以上就是从容大雁为你收集整理的2020年CCPC秦皇岛站部分题解前言A Greeting from Qinhuangdao(组合数学)Exam Results(枚举+贪心)Friendly Group(并查集)后话的全部内容，希望文章能够帮你解决2020年CCPC秦皇岛站部分题解前言A Greeting from Qinhuangdao(组合数学)Exam Results(枚举+贪心)Friendly Group(并查集)后话所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。