拓扑排序算法详讲

42 阅读 0 评论 28 点赞

我是靠谱客的博主紧张香水，最近开发中收集的这篇文章主要介绍拓扑排序算法详讲，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

经过一天的专研,终于明白了拓扑排序算法,写篇博客记录一下心得.

一.拓扑排序介绍

在一个表示工程的有向图中,用顶点表示活动,用弧表示活动之间的优先关系,这样的有向图为顶点表示活动的网,我们称为AOV网.
设G=(V,E)是一个具有n个顶点的有向图,v中的顶点序列v1,v2…,vn,满足若从顶点到v1到vj有一
条路径,则在顶点序列中顶点vi必须在顶点vj之前,我们称这样的顶点序列为一个拓扑序列.
所谓拓扑排序,其实就是对一个有向图构造拓扑序列的过程,.
构造时会有两个结果,如果此网的全部顶点都被输出,则说明它是不存在环的AOV网;如果输出的顶点数少了,哪怕是少了一个,也说明这个网存在环,不是AOV网.
一个不存在回路的AOV网,我们可以将它应用在各种各样的工程或项目的流程图中,满足各种应用场景的需要,所以实现拓扑排序很有价值.

二.拓扑排序算法实现

对AOV网进行拓扑排序的基本思路是：
1.从AOV网中选择一个入读为0的顶点输出，然后删去此顶点，并删除此顶点为尾的弧，
2.重复此步骤，直到输出全部顶点或者AOV网中不存在入度为0的顶点为止。

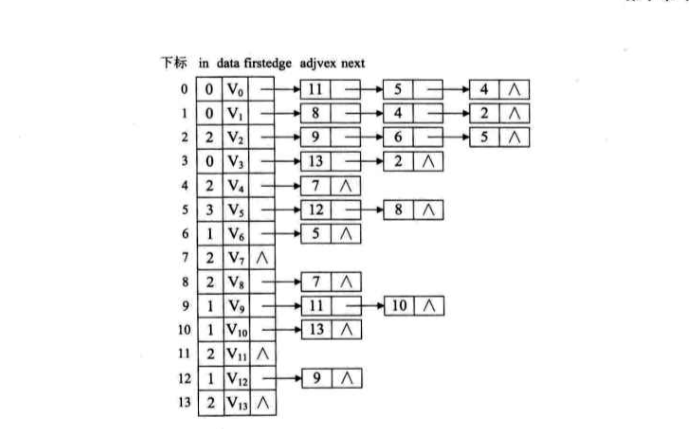
对于拓扑排序，在排序的过程中需要删除顶点，显然用邻接表会更加方便，因此我们需要为AOV网建立一个邻接表。考虑到算法过程中始终需要查找入度为0的顶点，我们在原来顶点表结点结构中，需要增加一个入度域in，结构如表所示，其中in就是入读的数字。

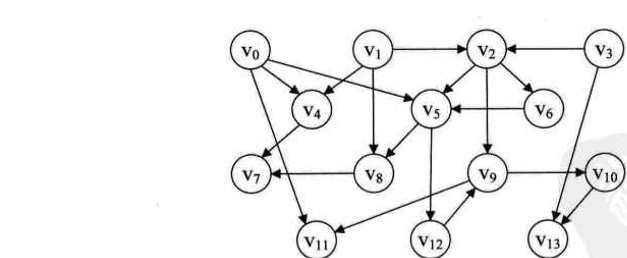
有了上面的介绍我们就可以把下面的AOV图转换为邻接表数据结构

#define MAXPOINT 100

typedef struct EdgeNode  //边表结点
{
	int index;  //邻接点的下标,
	struct EdgeNode * next;   //链域,指向下一个邻接点
	int weight;                  //权值
}EdgeNode;

typedef struct PointNode   //顶点表结点
{
	int in;                  //顶点入度.
	int data;                  //顶点信息
	EdgeNode *  firstEdge;   //边表头指针.   
}PointNode;

typedef struct Graph
{
	
	int NumPoint, NumEdge;
	PointNode arr[MAXPOINT];
}Graph;



void CreateGraph(Graph * G)
{
	int i, j, k;
	EdgeNode* e;
	printf("请输入顶点和弧的数目:n");
	scanf("%d %d", &G->NumPoint, &G->NumEdge);
	printf("请输入各个顶点的信息:n");
	for (i = 0; i < G->NumPoint; i++)
	{
		scanf("%d", &G->arr[i].data);
		G->arr[i].in=0;
		G->arr[i].firstEdge = NULL;
	}
	for (k = 0; k < G->NumEdge; k++)
	{
		printf("请输入弧<vi,vj>上的信息:n");
		scanf("%d %d", &i, &j);
		e = (EdgeNode*)malloc(sizeof(EdgeNode));
		e->index = j;
	
		e->next = G->arr[i].firstEdge;
		G->arr[i].firstEdge = e;
		G->arr[j].in++;
	}
}
int ToupuSort(Graph* G)
{
	//我们需要辅助的数据结构-栈,  用来存储处理过程中入度为0的顶点
	//目的是为了避免每个查找时都要全部遍历顶点表找入度为0的顶点.
	
	EdgeNode *e;
	int i,  k, gettop;
	int top = -1;
	int count = 0;
	int * stack;
	stack = (int *)malloc(sizeof(int)*G->NumPoint);
	for (i = 0; i < G->NumPoint; i++)
	{
		if (G->arr[i].in == 0)
			stack[++top] = i;
	}
	while (top != -1)
	{
		gettop = stack[top--];
		printf("%d->", G->arr[gettop].data);
		count++;
		for (e = G->arr[gettop].firstEdge; e; e = e->next)
		{
			k = e->index;
			if (!(--G->arr[k].in))
				stack[++top] = k;
		}

	}

	if (count < G->NumPoint)
		return -1;
	else
		return 0;

}

int main()
{
	Graph G;
	CreateGraph(&G);
	ToupuSort(&G);
	system("pause");
	return 0;

}