CCF202009-4 星际旅行（100分题解链接）

试题编号： 202009-4
试题名称： 星际旅行
时间限制： 1.0s
内存限制： 256.0MB
问题描述：

问题描述

在一个n维欧几里得空间的宇宙中，小 A 打算完成一次星际旅行。

利用n维直角坐标系，宇宙中每个点的位置都可以用n维坐标来表示。其中，在宇宙中心的O点（未必是坐标系原点）处，有一个半径为r的超球体黑洞，任何物体若落入黑洞内部（不包括其表面）则无法逃脱。

小 A 选定了m个不在黑洞内部的点P1,P2,…,Pm，作为他星际旅行的目标。不会有两个点处于同一位置。

为了提前做好旅行规划，小 A 希望求出这m个点两两之间的最短曲线距离。同样地，这些曲线不能经过黑洞的内部。为了方便，你只需要输出每个点到其他m-1个点的距离之和。

输入格式

第一行两个整数n,m。

第二行一个整数r。

第三行n个整数，依次表示超球体黑洞的中心O的每一维坐标。

接下来m行，每行n个整数。第i行的各个整数依次表示点Pi的每一维坐标。

同一行内的多个整数之间用一个空格隔开。

输出格式

输出一共m行，每行一个实数。第i行表示第i个点（Pi）到其他所有点的最短曲线距离之和。

请以“整数部分、小数点、小数部分”的格式输出实数，并保留不少于 12 位小数结果。采用其他格式（如科学记数法）输出可能无法得分。

样例输入1

2 3
2
3 1
5 1
1 3
3 -2

样例输出1

8.83711594354348
10.83711594354348
9.39104657990738

样例1说明

如下图所示，圆O为二维平面上的黑洞，P1,P2,P3为小 A 星际旅行的目标。

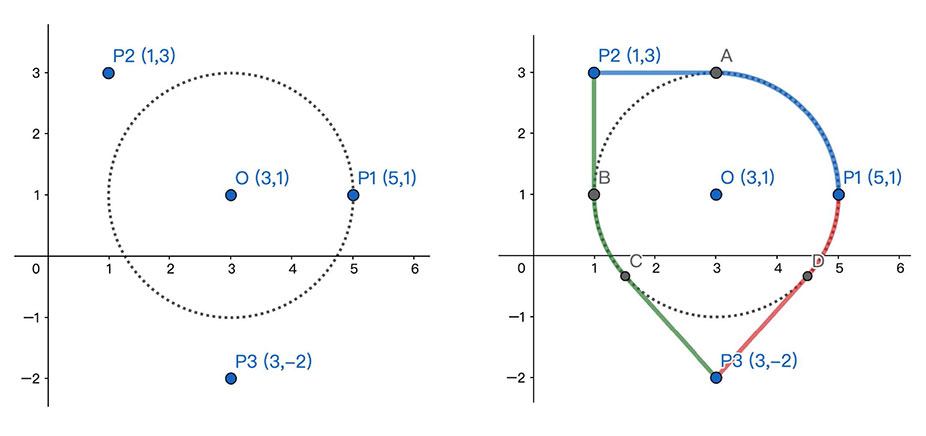
通过在圆周上选择合适的点A,B,C,D，可以证明，
曲线P1AP2,P2BCP3,P3DP1分别为这三对点之间满足条件的最短曲线。
这些曲线的长度分别为 5.14159265358979, 5.69552328995369, 3.69552328995369。

样例输入2

3 8
1
0 0 0
0 0 1
0 1 0
1 0 0
1 1 1
-1 -1 0
-1 0 -1
0 -1 -1
-1 -1 -1

样例输出2

14.12797001266400
14.12797001266400
14.12797001266400
17.90086240651788
13.95502966750398
13.95502966750398
13.95502966750398
14.99490548122857

评分方法

对于每个测试点，你的结果正确则得该测试点的满分，错误不得分。你的输出被认为是正确的，当且仅当你输出的每个实数与对应答案的相对或绝对误差不超过10^-9。

为了达到这一精度要求，请不要使用单精度浮点数（对应 C、C++、Java 语言的 float 类型，机器精度约10^-6级别）完成本题，而应当使用双精度浮点数（对应 C、C++、Java 语言的 double 类型、Python 语言的 float 类型，机器精度约10^-15级别）或更精确的表示法（如整数类型 int，前提是不能超出该类型的表示范围）。

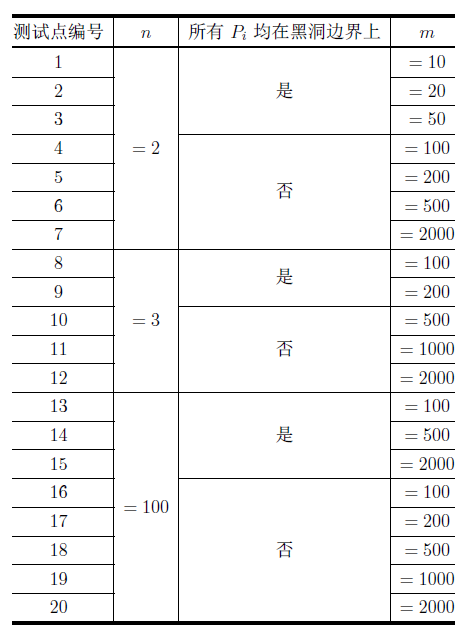
评测用例规模与约定

本题共 20 个测试点，每个 5 分。

对于所有的测试点，2≤n≤100,2≤m≤2000,1≤r≤1000.

输入中的所有坐标均在[-1000,1000]范围内。

提示

以下数学知识对你求解此题有可能会有帮助（其中所有的角均采用弧度制）：

·某个点在超球体的内部（不含边界），当且仅当该点到球心的距离小于超球体的半径；
·超球体的任意一条切线（与超球体有且仅有一个公共点的直线）垂直于过切点的半径；
·给定实数A1,A2,…,An,B（其中A1,A2,…,An不全为 0），方程A1x1+A2x2+…+Anxn+B=0确定了n维空间中的一个n-1维超平面，向量(A1,A2,…,An)是该超平面的一个法向量，点(p1,p2,…,Pn)到该超平面的距离为：
$$\frac{|A_1{p}_1+A_2{p}_2+...+A_n{p}_n+B|}{\sqrt{A_1^2+A_2^2+...+A_n^2}}$$
·对于半径为r的圆，圆心角α对应的弧长为αr；
·对于三边长分别为a,b,c的三角形 ABC（边a是点A的对边，其余同）：
○正弦定理：$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=D$，其中D为三角形外接圆直径；
○余弦定理：$c^2=a^2+b^2-2abcosC$；
○正弦求三角形面积：$S=\frac{1}{2}absinC$；
○海伦-秦九韶公式：$S=\sqrt{p(p-a)(p-b)(p-c)}$，其中p=(a+b+c)/2；
·同上述，如果$C=\frac{\pi }{2}$，该三角形为直角三角形：
○勾股定理：$a^2+b^2=c^2$；
○三角函数定义：正弦$sinA=\frac{a}{c}$，余弦$cosA=\frac{b}{c}$，正切$tanA=\frac{a}{b}$；
·三角函数的和/差角公式：
○ 两角和/差的正弦：$sin(\alpha \pm \beta )=sin\alpha cos\beta \pm cos\alpha sin\beta$；
○两角和/差的余弦：$cos(\alpha \pm \beta )=cos\alpha cos\beta \pm sin\alpha sin\beta$；
○两角和/差的正切：$tan(\alpha \pm \beta )=\frac{tan\alpha \pm tan\beta }{1\pm tan\alpha tan\beta }$。

问题链接：CCF202009-4 星际旅行
问题简述：（略）
问题分析：（略）
程序说明：（略）
参考链接：
第二十次csp认证 第四题 星际旅行题解
CCFCSP认证202009-4星际旅行满分题解（C++）
CCF CSP认证 202009-4 星际旅行
202009-4 星际旅行
202009-4 星际旅行
题记：（略）

100分的C++语言程序如下：

最后

以上就是无私鞋子为你收集整理的CCF202009-4 星际旅行（100分题解链接）的全部内容，希望文章能够帮你解决CCF202009-4 星际旅行（100分题解链接）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。