LeetCode 1573. 分割字符串的方案数（组合数学）

题意：

给你一个二进制串 s  （一个只包含 0 和 1 的字符串），
我们可以将 s 分割成 3 个 非空 字符串 s1, s2, s3 （s1 + s2 + s3 = s）。

请你返回分割 s 的方案数，满足 s1，s2 和 s3 中字符 '1' 的数目相同。

由于答案可能很大，请将它对 10^9 + 7 取余后返回。

数据范围:
s[i] == '0' 或者 s[i] == '1'
3 <= s.length <= 10^5

解法：

设tot为1的总数量,
如果tot=0,那么答案为C(n-1,2),
如果tot!=0,那么:
设串下标为[1,n],
找到满足s[1,l]=tot/3的最小下标l,
找到满足s[r,n]=tot/3的最大下标r,
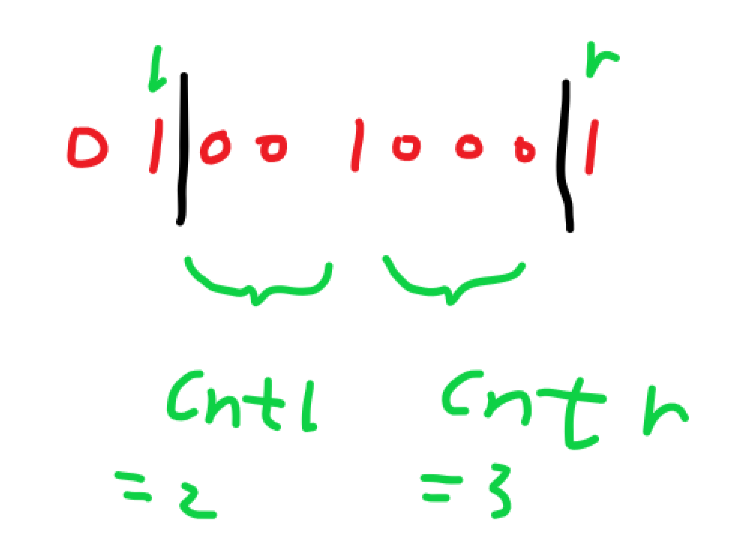
然后统计l+1开始到其右边第一个1之间0的数量cntl,
以及r-1开始到其左边第一个1之间0的数量cntr.

那么答案为(cntl+1)*(cntr+1),
因为左边有cntl+1个空隙可以选择,
右边有cntr+1个空隙可以选择.

如下图:

code：

class Solution {
public:
    static const int maxm=1e5+5;
    static const int mod=1e9+7;
    int d[maxm];
    int numWays(string s) {
        memset(d,0,sizeof d);
        int n=s.size();
        s='p'+s;
        int ans=0;
        for(int i=1;i<=n;i++){
            d[i]=d[i-1]+(s[i]=='1');
        }
        int tot=d[n];
        if(tot==0){
            return 1ll*(n-1)*(n-2)/2%mod;
        }
        if(tot%3)return 0;
        int l=1;
        while(d[l]!=tot/3)l++;
        int r=n;
        while(d[n]-d[r-1]!=tot/3)r--;
        int cntl=0,cntr=0;
        for(int i=l+1;i<=n;i++){
            if(s[i]=='0')cntl++;
            else break;
        }
        for(int i=r-1;i>=1;i--){
            if(s[i]=='0')cntr++;
            else break;
        }
        return 1ll*(cntl+1)*(cntr+1)%mod;
    }
};

最后

以上就是彪壮毛衣为你收集整理的LeetCode 1573. 分割字符串的方案数（组合数学）的全部内容，希望文章能够帮你解决LeetCode 1573. 分割字符串的方案数（组合数学）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。