1. 首页
  2. 文章中心
  3. 数据结构与算法

【数据结构】Leetcode——回溯算法：排列问题/棋盘问题

75 阅读 0 评论
我是靠谱客的博主 大胆八宝粥，最近开发中收集的这篇文章主要介绍【数据结构】Leetcode——回溯算法：排列问题/棋盘问题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Contents

    • 1 全排列(46)
    • 2 全排列 II(47)
    • 3 重新安排行程(332)
    • 4 N皇后问题(51)
    • 5 解数独(37)
    • 补：6 子集 II(90)
    • 补：7 递增子序列（491）

开始之前学习一个单词热热身：

fetch 英[fetʃ]
v. (去) 拿来; (去) 请来; 售得，卖得(某价);
[例句]Sylvia fetched a towel from the bathroom
西尔维娅去卫生间拿了一条毛巾。

1 全排列(46)

题目：
     给定一个 没有重复数字的序列，返回其所有可能的全排列。
示例：

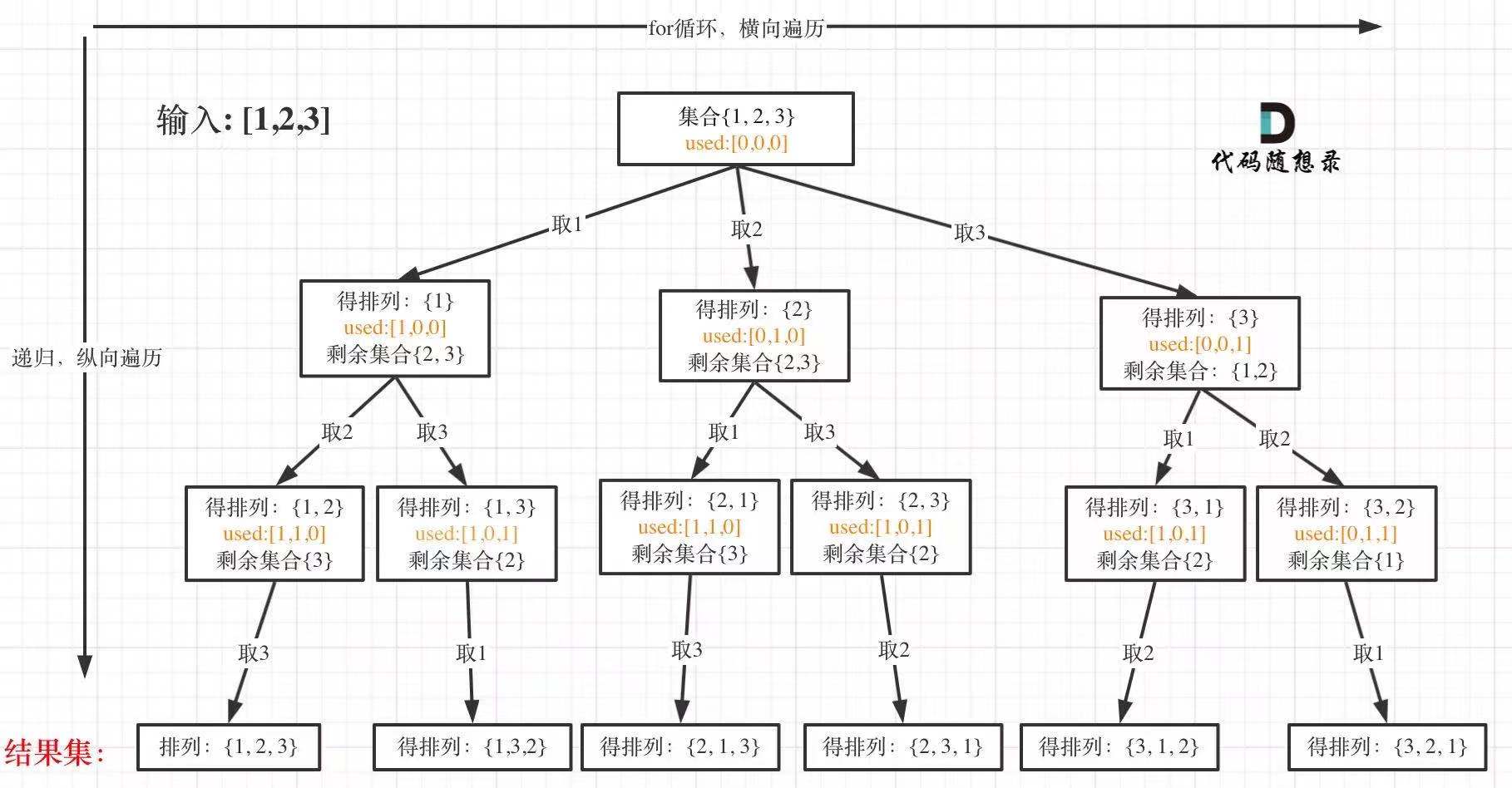
在这里插入图片描述
思路：
在这里插入图片描述

     排列是有序的，即[1, 2] 与[2, 1]是两个不同的集合，故不需要参数startIndex参数了、
     使用vector<bool>& used数组来标记集合中的元素是否使用过。

class Solution {
private:
    vector<int> path;
    vector<vector<int>> res;
    void backtracking(vector<int>& nums, vector<bool>& used){
        if(path.size()==nums.size()){
            res.push_back(path);
            return;
        }
        for(int i=0; i<nums.size(); i++){
            if(used[i]==true) continue;
            used[i]=true;
            path.push_back(nums[i]);
            backtracking(nums, used);
            path.pop_back();
            used[i]=false;
        }
    }
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<bool> used(nums.size(), false);
        backtracking(nums, used);
        return res;
    }
};

排列问题的不同：

  • 每层都是从0开始搜索而不是startIndex；
  • 需要used数组来标记path中都放入了哪些元素。

2 全排列 II(47)

题目：
     给定一个 可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。
示例：
在这里插入图片描述
思路：
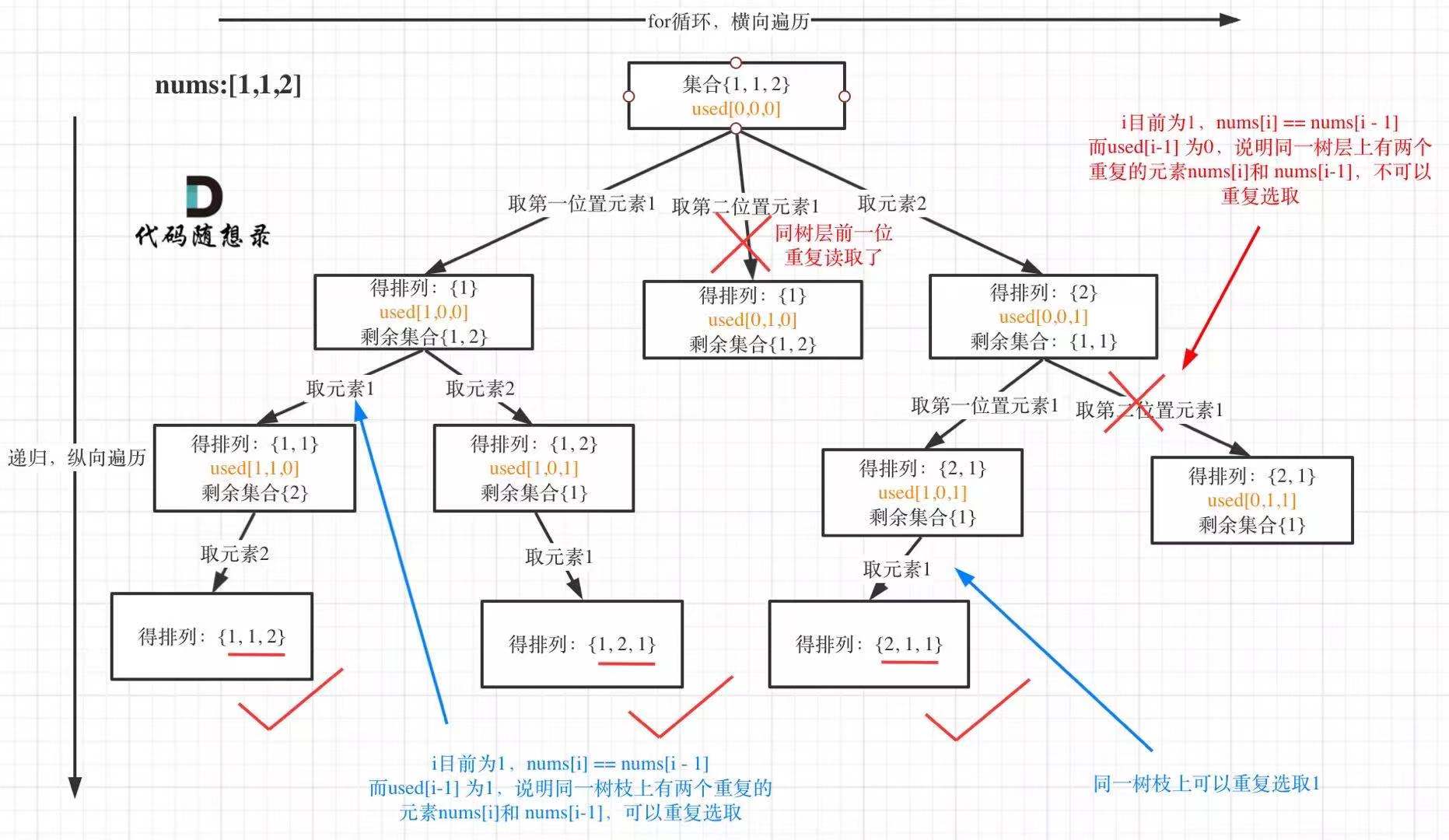
     给定序列包含重复元素，则在回溯过程中需要去重，关键一行代码为：

 if(i>0 && nums[i]==nums[i-1] && used[i-1]==false) continue;
  • used[i-1]==false表示同一树层中，去掉path中同一开始相同元素。
  • 要注意一旦涉及到去重，就必须对给定序列进行排序，为的是满足去重条件中的nums[i]==nums[i-1]
  • 与上一题相同，本题同样也不需要startIndex参数。

在这里插入图片描述

class Solution {
private:
    vector<int> path;
    vector<vector<int>> res;
    void backtracking(vector<int>& nums, vector<bool>& used){
        if(path.size()==nums.size()){
            res.push_back(path);
            return;
        }
        for(int i=0; i<nums.size(); i++){
            // 这里理解used[i - 1]非常重要 
            // used[i - 1] == true，说明同一树支nums[i - 1]使用过 
            // used[i - 1] == false，说明同一树层nums[i - 1]使用过
            // 如果同一树层nums[i - 1]使用过则直接跳过
            if(i>0 && nums[i]==nums[i-1] && used[i-1]==false) continue;
            if(used[i]==false){
	            used[i]=true;
	            path.push_back(nums[i]);
	            backtracking(nums, used);
	            path.pop_back();
	            used[i]=false;
            }
        }
    }
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<bool> used(nums.size(), false);
        sort(nums.begin(), nums.end()); //有去重的话一定要先排序
        backtracking(nums, used);
        return res;
    }
};

3 重新安排行程(332)

题目：
     给定一个机票的字符串二维数组 [from, to]，子数组中的两个成员分别表示飞机出发和降落的机场地点，对该行程进行重新规划排序。所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。

     如果存在多种有效的行程，请你按字符自然排序返回最小的行程组合。例如，行程["JFK", "LGA"]与["JFK", "LGB"]相比就更小，排序更靠前。

示例：
在这里插入图片描述
思路：
1、记录机场间的映射关系
unordered_map<string, map<string, int>> targets;
     可理解为：unordered_map<出发机场, map<到达机场, 航班次数>> targets，其中的map类型是为了满足题中"按字符自然排序"的要求（因为map中存储数据是默认有序的）。

2、死循环问题
     出发机场和到达机场也会重复，如下图。故使用int型数据来标识航班次数，避免死循环。
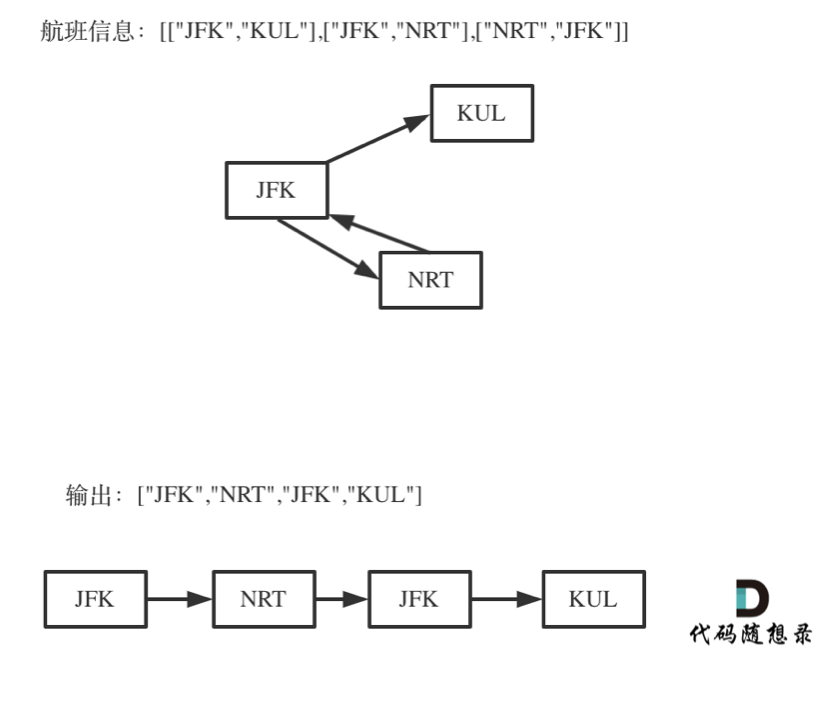
在这里插入图片描述
3、回溯函数返回值
     这里的回溯函数返回值使用bool型，因为本次只需要找到一个行程，就是在树形结构中唯一的一条通向叶子节点的路线，找到了这个叶子节点时直接返回即可，故返回值为bool。

class Solution {
private:
    unordered_map<string, map<string, int>> targets;
    vector<string> result;
    bool backtracking(int ticketNum, vector<string>& result){
        if(result.size()==ticketNum+1){
            return true;
        }
        for(pair<const string, int>& target: targets[result[result.size()-1]]){ //有一种不断连接机票的感觉
            if(target.second>0){
                result.push_back(target.first);
                target.second--;
                if(backtracking(ticketNum, result)) return true;
                result.pop_back();
                target.second++;
            }
        }
        return false;
    }
public:
    vector<string> findItinerary(vector<vector<string>>& tickets) { 
        for(const vector<string>& vec: tickets){
            targets[vec[0]][vec[1]]++;
        }
        result.push_back("JFK");
        backtracking(tickets.size(), result);
        return result;
    }
};

4 N皇后问题(51)

题目：
     n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。
     每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

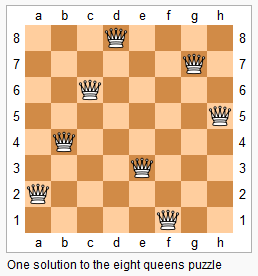
在这里插入图片描述
示例：
在这里插入图片描述
思路：
1、判断将皇后放在棋盘上的某个位置是否有效；
不能同行 / 不能同列 / 不能同斜线（45°和135°）
注意：
     在单层搜索的过程中，每一层横向递归，只会选for循环（也就是同一行）里的一个元素，所以不用检查行方向上有无重复’Q’（因为在每一行中，'Q’只会放在某一个单元格中后进而纵向递归）。
判断有效的函数如下：

    bool isValid(int row, int col, vector<string>& chessboard, int n){
        //检查列
        for(int i=0; i<row; i++){
            if(chessboard[i][col] == 'Q') return false;
        }
        //检查45度角是否有皇后
        for(int i=row-1, j=col-1; i>=0 && j>=0; i--, j--){
            if(chessboard[i][j] == 'Q') return false;
        }
        //检查135度角是否有皇后
        for(int i=row-1, j=col+1; i>=0 && j<n; i--, j++){
             if(chessboard[i][j] == 'Q') return false;
        }
        return true;
    }

2、递归回溯过程

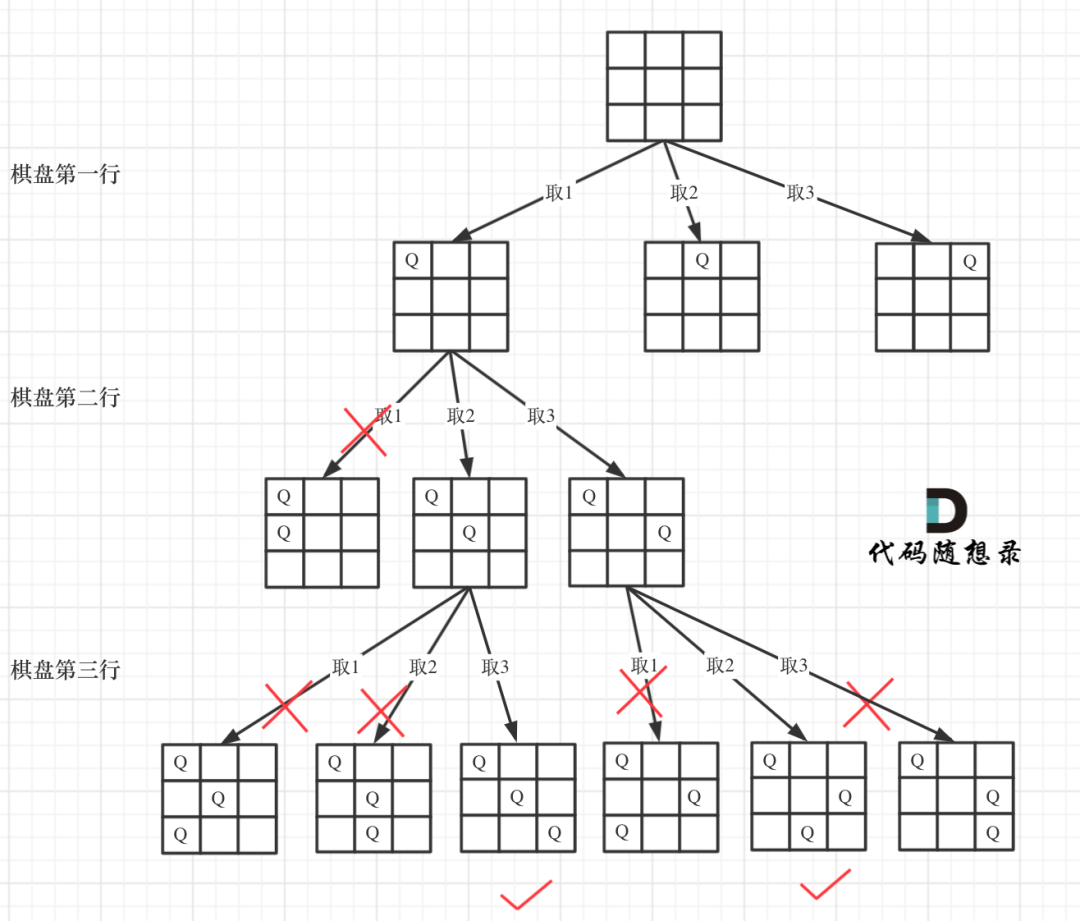
在这里插入图片描述
     由上图可以看出，递归横向和纵向遍历的宽度均等于n，其中横向遍历由for循环实现，纵向遍历由回溯实现。
     递归深度就是row控制棋盘的行，每一层里for循环的col控制棋盘的列，一行一列，确定了放置皇后的位置。

class Solution {
private:
    vector<vector<string>> result;
    // n 为输入的棋盘大小
    // row 是当前递归到棋牌的第几行了
    bool isValid(int row, int col, vector<string>& chessboard, int n){
        //检查列
        for(int i=0; i<row; i++){
            if(chessboard[i][col] == 'Q') return false;
        }
        //检查45度角是否有皇后
        for(int i=row-1, j=col-1; i>=0 && j>=0; i--, j--){
            if(chessboard[i][j] == 'Q') return false;
        }
        //检查135度角是否有皇后
        for(int i=row-1, j=col+1; i>=0 && j<n; i--, j++){
             if(chessboard[i][j] == 'Q') return false;
        }
        return true;
    }
    void backtracking(int n, int row, vector<string>& chessboard){
        if(row==n){
            result.push_back(chessboard);
            return;
        }
        for(int col=0; col<n; col++){
            if(isValid(row, col, chessboard, n)) {
                chessboard[row][col] = 'Q';
                backtracking(n, row+1, chessboard);
                chessboard[row][col] = '.';
            }
        }
    }
public:
    vector<vector<string>> solveNQueens(int n) {
        vector<string> chessboard(n, string(n, '.'));
        backtracking(n, 0, chessboard);
        return result;
    }
};

5 解数独(37)

题目：
在这里插入图片描述
示例：
在这里插入图片描述
思路：
1、判断将1~9中的某个数放在某行某列确定的格子中是否有效；
不能同行重复 / 不能同列重复 / 不能9宫格重复

    bool isValid(int row, int col, char val, vector<vector<char>>& board){
        for(int i=0; i<9; i++){ // 判断列里是否重复
            if(board[i][col]==val) return false;
        }
        for(int j=0; j<9; j++){ // 判断行里是否重复
            if(board[row][j]==val) return false;
        }
        int startRow = (row / 3) * 3;
        int startCol = (col / 3) * 3;
        for(int i=startRow; i<startRow+3; i++){
            for(int j=startCol; j<startCol+3; j++){
                if(board[i][j]==val) return false;
            }
        }
        return true;
    }

2、二维递归
     N皇后问题是因为每一行只放一个皇后，只需要一层for循环遍历一行，递归用来遍历列，然后一行一列确定皇后的唯一位置。而本题中棋盘的每一个位置都要放一个数字，并检查数字是否合法，解数独的树形结构要比N皇后更宽更深」。
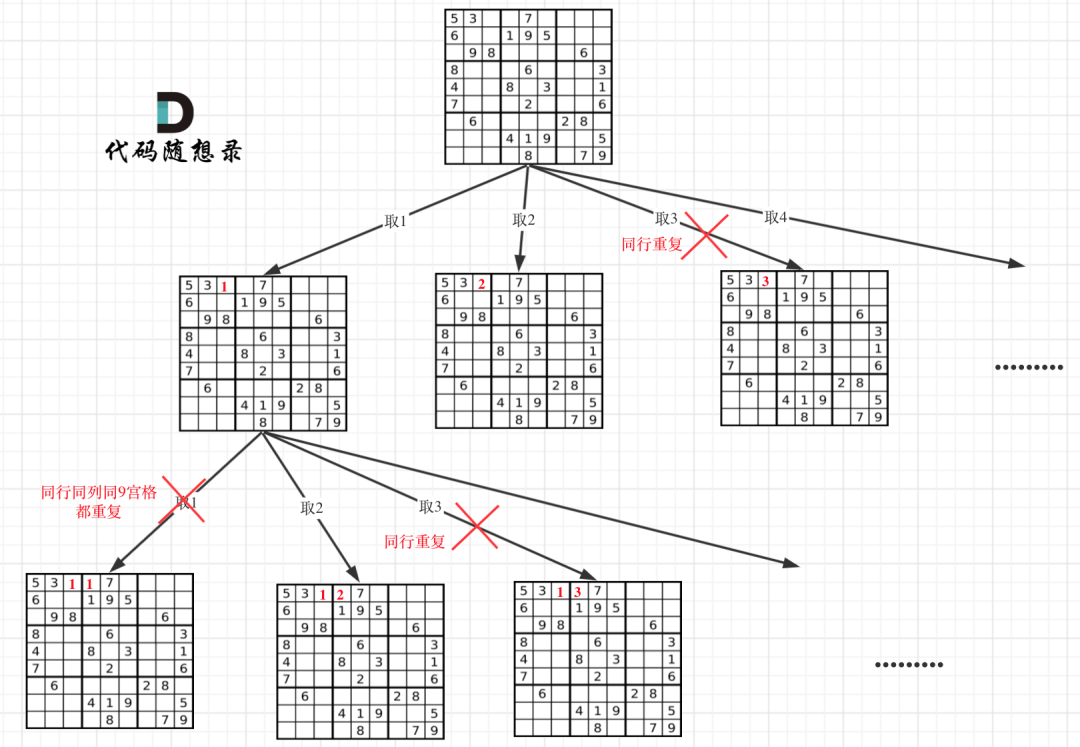
在这里插入图片描述
回溯函数中没有条件判断终止语句的原因：

     回溯函数中的return false的地方是很有讲究的：因为如果一行一列确定下来了，这里尝试了9个数都不行，说明这个棋盘找不到解决数独问题的解！
     那么会直接返回， 「这也就是为什么没有终止条件也不会永远填不满棋盘而无限递归下去！」

class Solution {
private:
    bool isValid(int row, int col, char val, vector<vector<char>>& board){
        for(int i=0; i<9; i++){ // 判断列里是否重复
            if(board[i][col]==val) return false;
        }
        for(int j=0; j<9; j++){ // 判断行里是否重复
            if(board[row][j]==val) return false;
        }
        int startRow = (row / 3) * 3;
        int startCol = (col / 3) * 3;
        for(int i=startRow; i<startRow+3; i++){
            for(int j=startCol; j<startCol+3; j++){
                if(board[i][j]==val) return false;
            }
        }
        return true;
    }
    bool backtracking(vector<vector<char>>& board){
        for(int i=0; i<9; i++){ // 遍历行
            for(int j=0; j<9; j++){ // 遍历列
                if(board[i][j] != '.') continue; 
                for(char k='1'; k <='9'; k++){  // (i, j) 这个位置放k是否合适
                    if(isValid(i, j, k, board)){
                        board[i][j] = k;
                        if(backtracking(board)) return true;
                        board[i][j] = '.';
                    }
                }
                return false; // 9个数都试完了，都不行，那么就返回false
            }
        }
        return true;
    }
public:
    void solveSudoku(vector<vector<char>>& board) {
        backtracking(board);
    }
};

补：6 子集 II(90)

题目：
     给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。
     解集不能包含重复的子集。
示例：
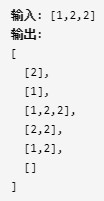
在这里插入图片描述
思路：
     本题和上一题的区别是给定集合中包含重复元素，故在回溯时需要去重，否则解集中会包含重复子集。
     基于子集(78)加上去重就好啦！去重的方式还是采用组合总和 II(40，集合有重复元素、数字不可重复选取)中的方法，即引入vector<bool> used;：

    // used[i - 1] == true，说明同一树支candidates[i - 1]使用过
    // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
    // 要对同一树层使用过的元素进行跳过

class Solution {
private:
    vector<int> path;
    vector<vector<int>> res;
    void backtracking(vector<int>& nums, int startIndex, vector<bool> used){
        res.push_back(path);
        if(startIndex>=nums.size()) return;
        for(int i=startIndex; i<nums.size(); i++){
            if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false) continue;
            path.push_back(nums[i]);
            used[i]=true;
            backtracking(nums, i+1, used);
            used[i]=false;
            path.pop_back();
        }
    }
public:
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        vector<bool> used(nums.size(), false);
        sort(nums.begin(), nums.end());
        backtracking(nums, 0, used);
        return res;
    }
};

补：7 递增子序列（491）

题目：
     给定一个整型数组, 你的任务是找到所有该数组的递增子序列，递增子序列的长度至少是2。
示例：
在这里插入图片描述
思路：
在这里插入图片描述

     本题和子集 II(90)中的去重有所不同，在上一题的去重首先需要将所给数组排序，而本题不可以改变给定数组顺序。取子序列问题仍可看为树形结构取节点路径问题，这里的去重逻辑为：

 if((!path.empty()&&nums[i]<path.back()) || myset.find(nums[i])!=myset.end()){
                continue;

     !path.empty()&&nums[i]<path.back()表示添加到path中的值必须满足递增条件，
     myset.find(nums[i])!=myset.end()表示去掉同一树层中的相同元素。

class Solution {
private:
    vector<int> path;
    vector<vector<int>> res;
    void backtracking(vector<int>& nums, int startIndex){
        if(path.size()>1) res.push_back(path);
        set<int> myset;
        for(int i=startIndex; i<nums.size(); i++){
            if((!path.empty()&&nums[i]<path.back()) || myset.find(nums[i])!=myset.end()){
                continue;
            }
            myset.insert(nums[i]);
            path.push_back(nums[i]);
            backtracking(nums, i+1);
            path.pop_back();
        }
    }
public:
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtracking(nums, 0);
        return res;
    }
};

小总结：
     重新安排行程(332)、N皇后问题(51)、解数独(37)三道特殊回溯题目与前面的组合问题、分割问题、全排列问题均有所不一样，其主要难点在于两个方面：一方面是如何构建特定的数据结构以存放符合特定问题描述的信息；另一方面是如何判断将某个值放入某个地方是否可行；还有一个方面是如何处理与常规问题不同的二维棋盘格问题。
     做完回溯一系列题目后，收获颇多，主要包括以下几个方面的子问题，十分有用。

  • 如何理解回溯法的搜索过程？
  • 什么时候用startIndex，什么时候不用？
  • 如何去重？如何理解"树枝去重"与"树层去重"？
  • 如何理解二维递归？

参考：本文学习记录参考<代码随想录>，包括插图及代码。

欢迎关注【OAOA】

最后

以上就是大胆八宝粥为你收集整理的【数据结构】Leetcode——回溯算法：排列问题/棋盘问题的全部内容，希望文章能够帮你解决【数据结构】Leetcode——回溯算法：排列问题/棋盘问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(50)

相关文章

【leetcode】字符串分割
【leetcode】字符串分割
LeetCode_131 分割回文串1、题目：分割回文串2、解题思路回溯三部曲3、代码
LeetCode_131 分割回文串1、题目：分割回文串2、解题思路回溯三部曲3、代码
LeetCode 1573. 分割字符串的方案数（组合数学）
LeetCode 1573. 分割字符串的方案数（组合数学）
leetcode-分割字符串的方案数
leetcode-分割字符串的方案数
【数据结构】Leetcode——回溯算法：排列问题/棋盘问题
【数据结构】Leetcode——回溯算法：排列问题/棋盘问题
求解密码问题C - RJ503求解密码问题
求解密码问题C - RJ503求解密码问题
回溯算法-切割问题
回溯算法-切割问题
【Leetcode 专题二（回溯专题）】组合、切割、子集、排序、棋盘、行程问题一、回溯4、排列问题5、棋盘问题6、行程问题
【Leetcode 专题二（回溯专题）】组合、切割、子集、排序、棋盘、行程问题一、回溯4、排列问题5、棋盘问题6、行程问题

评论列表共有 0 条评论

立即
投稿
返回
顶部