文章目录
- 第一章
- 分类变量
- 总体、样本、参数、统计量
- 数据的分类
- 按照所采用的计量尺度不同,可以将统计数据分为分类数据、顺序数据和数值型数据。
- 按照统计数据的收集方法,可以将统计数据分为观测数据和实验数据
- 按照被描述的对象与时间的关系,可以将统计数据分为截面数据和时间序列数据
- 第二章
- 抽样类型
- 简单随机抽样
- 分层随机抽样(类型抽样)
- 整群抽样
- 机械抽样(等距抽样、系统抽样)
- 多级抽样(概率比例抽样法)
- 方便抽样
- 定额抽样(配额抽样)
- 立意抽样(判断抽样)
- 滚雪球抽样
- 空间抽样
- 误差类型
- 随机误差
- 第三章 图和概念的区分
- 各种统计图的特点
- 第四章
- 第五章
- 总体均值置信区间
- 总体成数的置信区间
- 总体方差置信区间
- 样本容量的确定
- 第六章 假设检验
- 假设检验的两类错误
- 决策原则
- 总体均值的检验
- 总体比例检验
- 总体方差检验
第一章
分类变量
统计学中的变量(variables)大致可以分为数值变量(numrical)和分类变量(categorical)。
有序分类变量和无需分类变量的区别是:前者对于“比较”操作是有意义的,而后者对于“比较”操作是没有意义的。
总体、样本、参数、统计量
总体(Population):所研究的全部个体(数据)的集合,其中每一个个体也称为元素。
样本(Sample):从总体中抽取一部分元素的集合(例如,从社群中抽10名小伙伴,这10名就可以成为样本)
样本容量(Sample size):样本中所含个体的数量
参数:研究者想要了解的总体的某种特征值。所关心的参数主要有总体均值、总体标准差、总体比例等。研究总体目的
统计量:用来描述样本特征的概括性数字度量,它是根据样本数据计算出来的一些量,是样本的函数。
需要注意的重点是:【统计量对应样本】【参数对应总体】
数据的分类
按照所采用的计量尺度不同,可以将统计数据分为分类数据、顺序数据和数值型数据。
分类数据:只能归于某一类别的非数字型数据。例如:人口性别
顺序数据:只能归于某一有序类别的非数字型数据,例如:将产品分成不同的等级。
数值型数据:按数字尺度测量的观测值,
按照统计数据的收集方法,可以将统计数据分为观测数据和实验数据
观测数据:通过调查或观测而收集到的数据,是在没有对事物人为控制的条件下而得到的。
实验数据:在实验中控制实验对象而收集到的数据。
按照被描述的对象与时间的关系,可以将统计数据分为截面数据和时间序列数据
截面数据:在相同或近似相同的时间点上收集的数据。描述的是现象某一时刻的变化情况
时间序列数据:在不同时间上收集到的数据。描述的是现象随时间而变化的情况
第二章
抽样类型
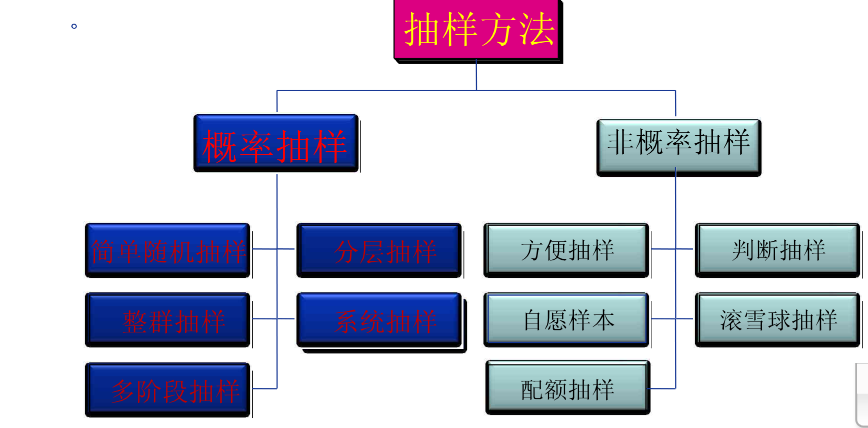
简单随机抽样
对总体不做任何处理,直接按照随机原则抽取调查单位。
分层随机抽样(类型抽样)
将总体按照某一主要标志进行分类(分组),在各类别中抽取一部分调查单位共同组成样本。(组内的个体差异较小时而各层的差异比较大)
整群抽样
将总体中若干个单位合并为组(群),抽样时直接抽取群,然后对中选群中的所有单位全部实施调查(组内个体存在差异)
机械抽样(等距抽样、系统抽样)
按某一标志对总体进行编号排队,然后确定抽样比例从而确定抽样间距。
多级抽样(概率比例抽样法)
对整群抽样的样本进行随机抽样
方便抽样
样本限于总体中易于抽到的一部分,某些调查对被调查者来说是不愉快的、麻烦的,这时为方便起见就采用以自愿被调查者为调查样本的方法。
定额抽样(配额抽样)
是将总体依某种标准分层(群);然后按照各层样本数与该层总体数成比例的原则主观抽取样本。
立意抽样(判断抽样)
研究人员从总体中选择那些被判断为最能代表总体的单位作样本的抽样方法.
滚雪球抽样
以若干个具有所需特征的人为最初的调查对象,然后依靠他们提供认识的合格的调查对象,再由这些人提供第三批调查对象,……依次类推。
空间抽样
对非静止的、暂时性的空间相邻的群体的抽样方法。
误差类型
随机误差
分析人员操作的微小差异以及仪器的不稳定等。它的特点:大小和方向都不固定,也无法测量或校正。随机误差的性质是:随着测定次数的增加,正负误差可以相互抵偿,误差的平均值将逐渐趋向于零,不会消除。
第三章 图和概念的区分
频数:在统计学中,将样本按照一定的方法分成若干组,每组内含有这个样本的个体的数目叫做频数.
比例:是一个总体中各个部分的数量占总体数量的比重,通常反映总体的构成和结构.
百分比:又称百分率、百分数(符号为%)是一种表达比例,比率或分数数值的方法,使用100作为分母.
比率:是各不同类别的数量的比值
各种统计图的特点
折线图(线图):能够显示数据的变化趋势,反应事物的变化情况(变化)
直方图(大批量):绘制连续性的数据,展示一组或多组数据的分布情况(统计)
条形图:绘制离散的数据,比较数据之间的差别
散点图:判断变量之间是否存在数量关联趋势,展示离群点(分布规律)
饼状图:适用于一个维度各项指标占总体的占比情况,分布情况。
茎叶图(小批量):它通常是作为更细致的分析阶段使用, 茎叶图从统计图上没有原始数据信息的损失,所有数据信息都可以从茎叶图中得到
雷达图:雷达图适用于展现多维数据集,一般是4-8个
箱线图:它主要展现了一组数据的几个关键数据点,包括最大值、最小值、中位数以及上下两个4分位数。一组数据按照从小到大顺序排列后,把该组数据四等分的数,称为四分位数;
气泡图:展示三个度量之间的相关关系,或者同时呈现三维数据
第四章
离散系数(变异系数):是测度数据离散程度的相对统计量,主要是用于比较不同样本数据的离散程度,C.V=标准差/平均数。
偏态系数:反映数据分布对称性的测度。等于零对称分布,大于零右偏分布(长尾在右),小于零左偏分布(长尾在左)。
峰态系数:对数据分布平峰或尖峰程度的测度,峰度的比较是通过正态分布来比较的。等于零正态分布,小于零扁平分布,大于零尖峰分布。
| 是否正态 | 比例范围 |
|---|---|
| 正态 | ±1,68% |
| 正态 | ±2,95% |
| 正态 | ±3,100% |
| 非正态 | ±2,75% |
| 非正态 | ±3,89% |
| 非正态 | ±4,99% |
第五章
总体成数:样本具有某一相同标志表现单位数占总体的比例
Π=N1/N; 成数方差:Π(1-Π)
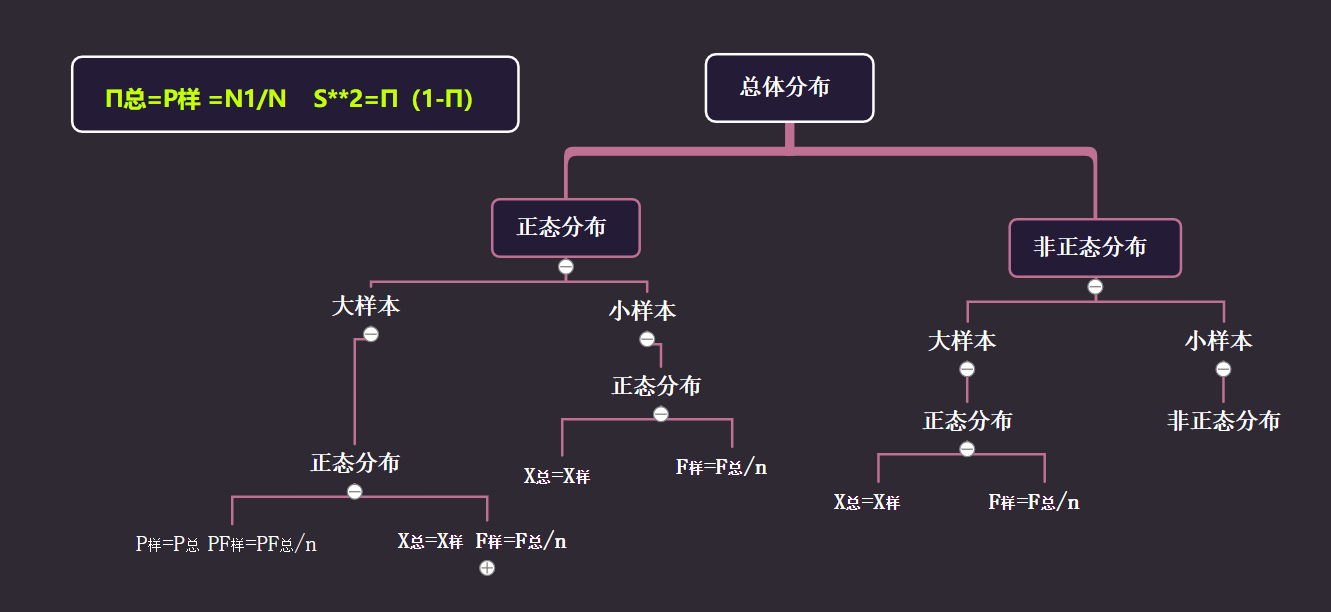
总体均值置信区间
- (1-a)称为置信度

总体成数的置信区间
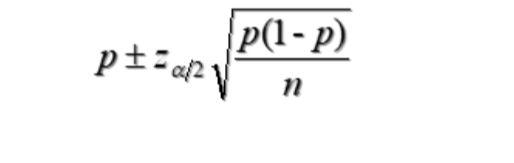
总体方差置信区间
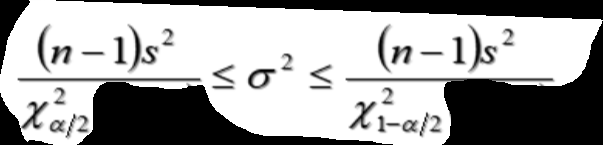
样本容量的确定

第六章 假设检验
- 假设检验的原理:小概率事件
- 原假设H0:反对研究者的假设
- 备择假设H1:支持研究者的假设
- H0和H1是一个完备事件组,互为对立事件
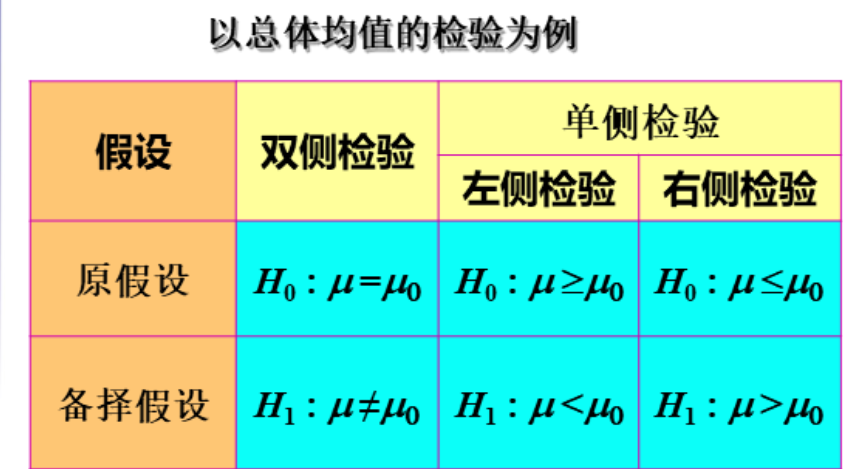
假设检验的两类错误
I:原假设正确被拒绝
II:原假设错误被接收
决策原则

总体均值的检验
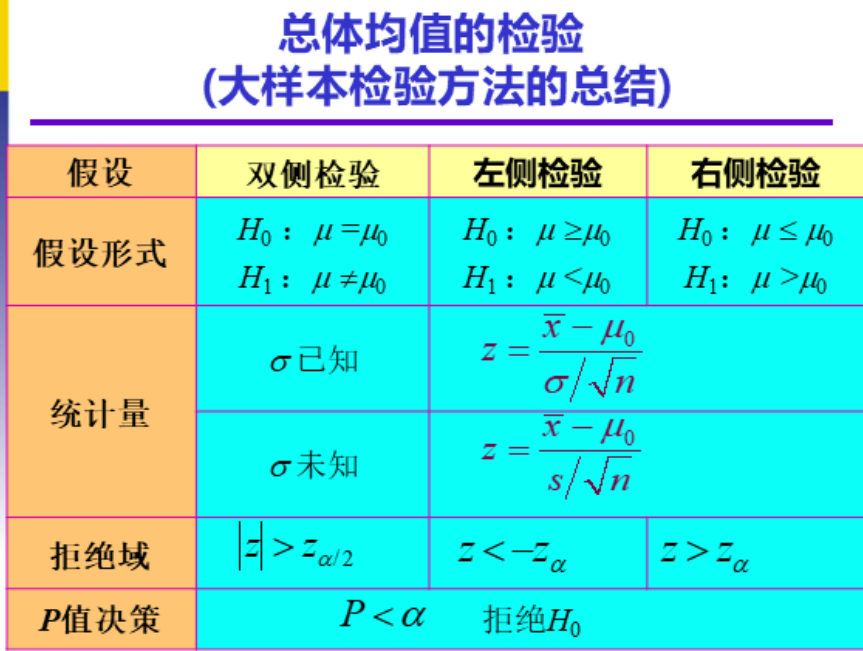
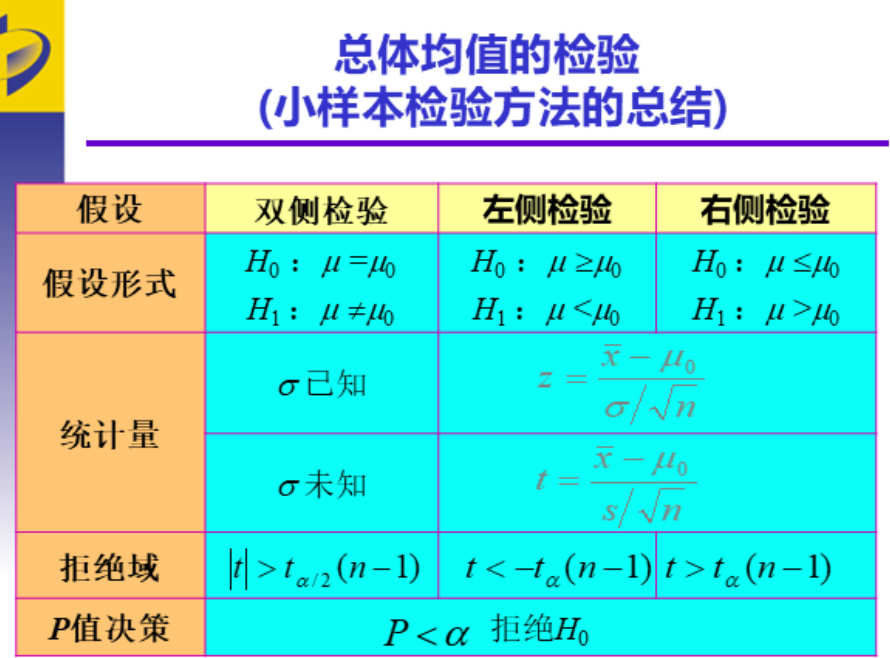
总体比例检验
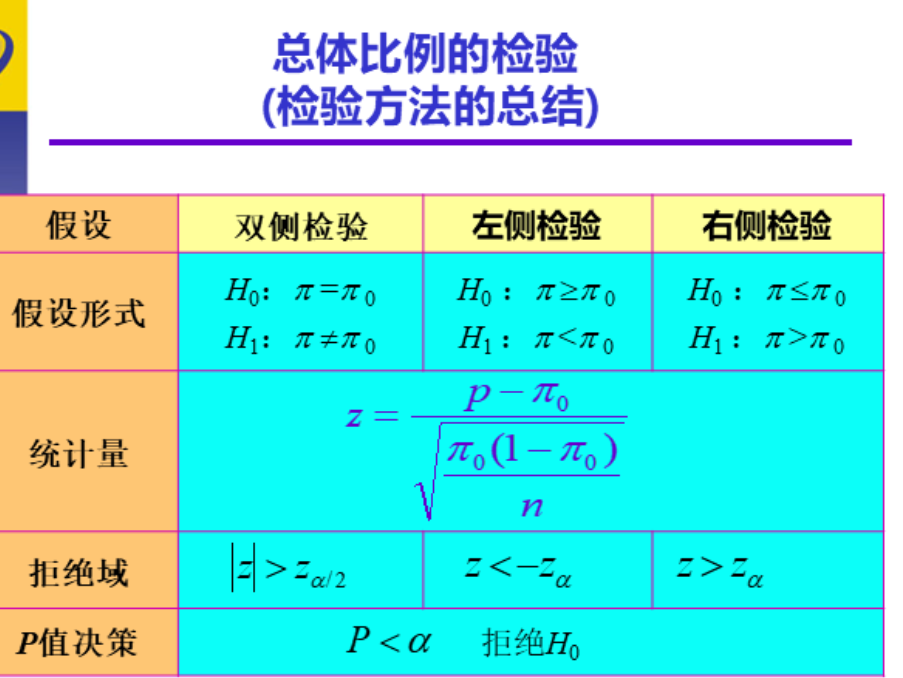
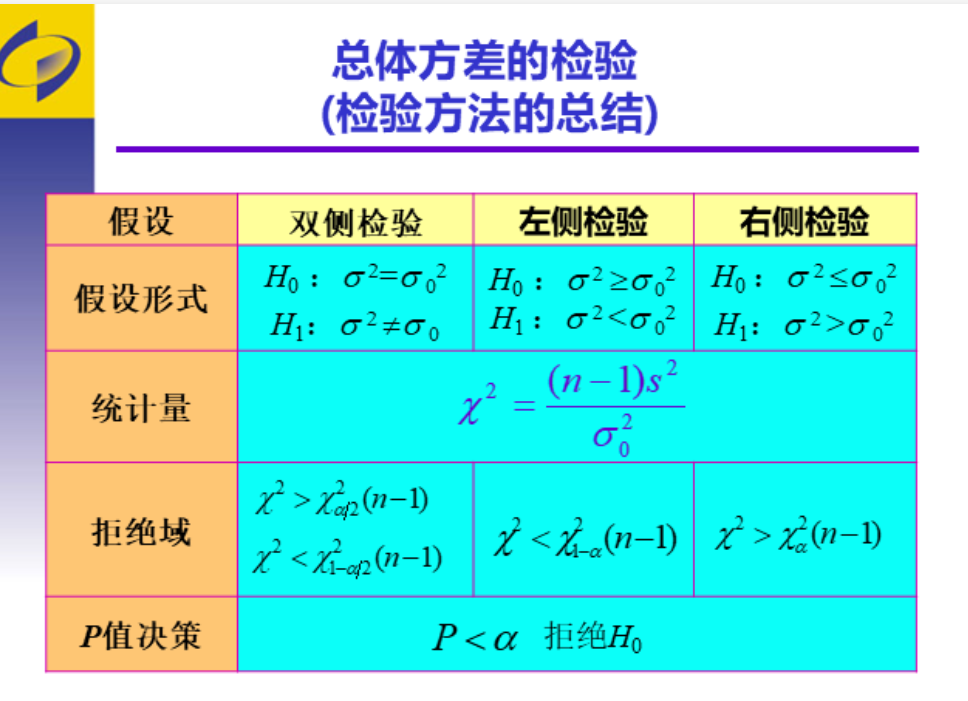
总体方差检验
最后
以上就是个性篮球最近收集整理的关于应用统计学知识整理第一章第二章第三章 图和概念的区分第四章第五章第六章 假设检验的全部内容,更多相关应用统计学知识整理第一章第二章第三章内容请搜索靠谱客的其他文章。








发表评论 取消回复